2018-2019学年山东省青岛市平度市七上期末数学试卷

这是一份2018-2019学年山东省青岛市平度市七上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. −12 的倒数是
A. −2B. 12C. ±12D. 2

2. 下列几何体的截面形状不可能是圆的是
A. 圆柱B. 圆锥C. 球D. 棱柱

3. 某数学兴趣小组为了解本校有多少学生已经患上近视，制定了四种抽样调查方案，你认为比较合理的调查方案是
A. 在校门口通过观察统计有多少学生
B. 在低年级学生中随机抽取一个班进行调查
C. 从每个年级的每个班随机抽取 1 名男生进行调查
D. 随机抽取本校每个年级 10% 的学生进行调查

4. 某大楼地上共有 12 层，地下共有 4 层．某人乘电梯从地下 2 层升至地上 9 层，电梯一共升了
A. 7 层B. 8 层C. 9 层D. 10 层

5. 若 x=y，则下列变形：① x+2=y+2；② −2x−1=−2y−1；③ xa=ya，正确的有
A. 0 个B. 1 个C. 2 个D. 3 个

6. 半径为 1 的圆中，扇形 AOB 的圆心角为 120∘，则扇形 AOB 的面积为
A. π6B. π3C. 2π3D. π

7. 小刚家 2017 年和 2018 年的家庭支出情况如图所示，则小刚家 2018 年教育方面支出的金额比 2017 年增加了
A. 0.216 万元B. 0.108 万元C. 0.09 万元D. 0.36 万元

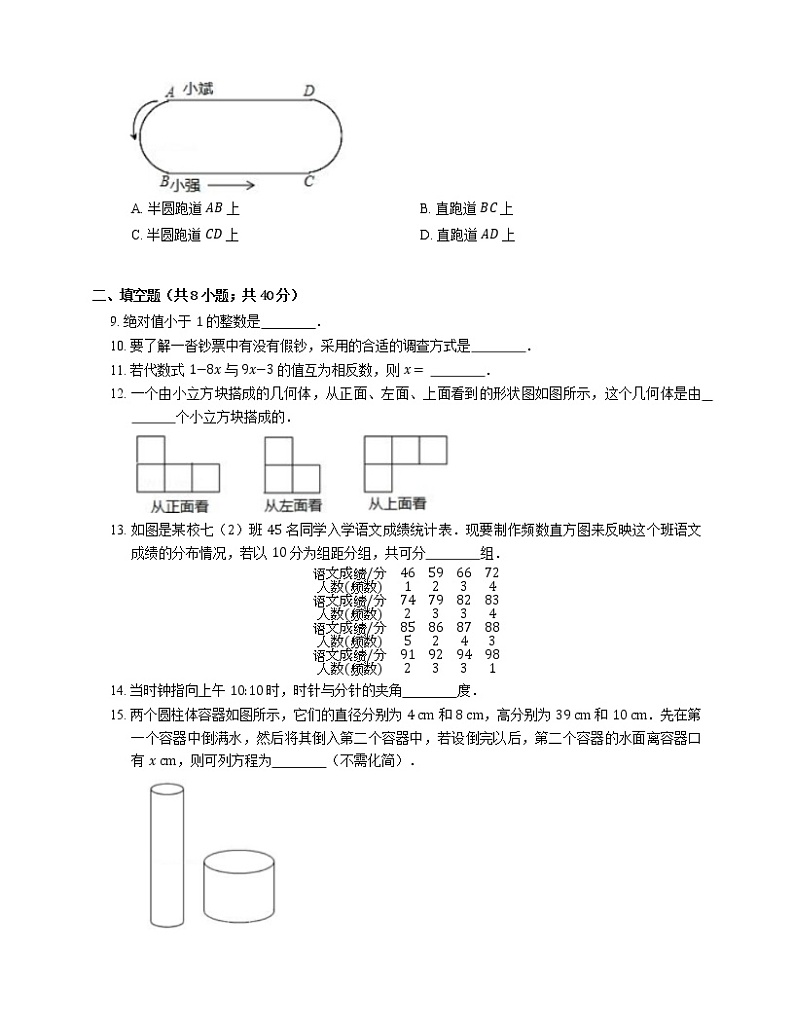
8. 如图，跑道由两个半圆部分 AB，CD 和两条直跑道 AD，BC 组成，两个半圆跑道的长都是 115 m，两条直跑道的长都是 85 m．小彬站在 A 处，小强站在 B 处，两人同时逆时针方向跑步，小彬每秒跑 4 m，小强每秒跑 6 m．当小强第一次追上小彬时，他们的位置在
A. 半圆跑道 AB 上B. 直跑道 BC 上
C. 半圆跑道 CD 上D. 直跑道 AD 上

二、填空题（共8小题；共40分）
9. 绝对值小于 1 的整数是 ．

10. 要了解一沓钞票中有没有假钞，采用的合适的调查方式是 ．

11. 若代数式 1−8x 与 9x−3 的值互为相反数，则 x= ．

12. 一个由小立方块搭成的几何体，从正面、左面、上面看到的形状图如图所示，这个几何体是由 个小立方块搭成的．

13. 如图是某校七（2）班 45 名同学入学语文成绩统计表．现要制作频数直方图来反映这个班语文成绩的分布情况，若以 10 分为组距分组，共可分 组．
语文成绩/分46596672人数频数1234语文成绩/分74798283人数频数2334语文成绩/分85868788人数频数5243语文成绩/分91929498人数频数2331

14. 当时钟指向上午 10:10 时，时针与分针的夹角 度．

15. 两个圆柱体容器如图所示，它们的直径分别为 4 cm 和 8 cm，高分别为 39 cm 和 10 cm．先在第一个容器中倒满水，然后将其倒入第二个容器中，若设倒完以后，第二个容器的水面离容器口有 x cm，则可列方程为 （不需化简）．

16. 一个两位数，若交换其个位数与十位数的位置，则所得的新两位数比原来两位数大 9．这样的两位数共有 个．

三、解答题（共8小题；共104分）
17. 已知：线段 a
求作：线段 AB，使 AB=2a．

18. 回答下列问题：
（1）计算：−5−−23+35÷−115；
（2）计算：−23×278÷323−13；
（3）化简：−2ab−3a2+5ab−a2；
（4）解方程：x−74−5x+83=1．

19. 如图，∠AOB 和 ∠COD 都是直角，射线 OE 是 ∠AOD 的平分线．
（1）比较 ∠AOC 和 ∠BOD 的大小，并说明理由；
（2）当 ∠BOC=130∘ 时，求 ∠DOE 的度数．

20. 如图，线段 AB=1，点 A1 是线段 AB 的中点，点 A2 是线段 A1B 的中点，点 A3 是线段 A2B 的中点 ⋯ 以此类推，点 An 是线段 An−1B 的中点．
（1）线段 A5B 的长为 ；
（2）线段 AnB 的长为 ；
（3）求 AA1+A1A2+A2A3+⋯+A7A8 的值．

21. 如图①是一张长为 20 cm，宽为 12 cm 的长方形硬纸板，把它的四个角都剪去一 个边长为 x cm 的小正方形，然后把它折成一个无盖的长方体盒子（如图②），请回答下列问题．
（1）折成的无盖长方体盒子的容积 V= cm3；（用含 x 的代数式表示即可，不需化简）
（2）请完成下表，并根据表格回答，当 x 取什么正整数时，长方体盒子的容积最大?
x/cm12345V/cm3180_252192_
（3）从正面看折成的长方体盒子，它的形状可能是正方形吗?如果是正方形，求出的值；如果不是正方形，请说明理由．

22. 某校对七年级 300 名学生进行了教学质量监测（满分 100 分），现从中随机抽取部分学生的成绩进行整理，并绘制成如图不完整的统计表和统计图：
等级频数频率频率=频数÷总数不及格10.05及格20.10良好_0.45优秀8_
注：60 分以下为“不及格”，60∼69 分为“及格”，70∼79 分为“良好”，80 分及以上为“优秀”
请根据以上信息回答下列问题：
（1）补全统计表和统计图；
（2）若用扇形统计图表示统计结果，则“良好”所对应扇形的圆心角为多少度?
（3）请估计该校七年级本次监测成绩为 70 分及以上的学生共有多少人?

23. 元旦期间，某商场用 1400 元购进了甲，乙两种商品，共 100 件，进价分别是 18 元，10 元．
（1）求甲，乙两种商品各购进了多少件?
（2）商场搞促销活动，若同时购买甲，乙两种商品各 1 件，可享受标价的 8 折优惠，此时这两种商品的利润率是 10%，求这两种商品的标价总共多少元?

24. 【问题】若 a+b=10，则 ab 的最大值是多少?
（1）【探究】
探究一：当 a−b=0 时，求 ab 值．
显然此时，a=b=5，则 ab=5×5=25．
探究二：当 a−b=±1 时，求 ab 值．
① a−b=1，则 a=b+1，
由已知得 b+1+b=10，
解得 b=92，
a=b+1=92+1=112，
则 ab=112×92=994．
② a−b=−1，即 b−a=1，由①可得，b=112，a=92，
则 ab=92×112=994．
探究三：当 a−b=±2 时，求 ab 值（仿照上述方法，写出探究过程）．
（2）探究四：完成下表：
a−b⋯−3−2−10123⋯ab⋯914—99425994——⋯
【结论】若 a+b=10，则 ab 的最大值是 （观察上面表格，直接写出结果）
【拓展】若 a+b=m，则 ab 的最大值是 ．
【应用】用一根长为 12 m 的铁丝围成一个长方形，这个长方形面积的最大值是 m2．
答案
第一部分
1. A【解析】−12 的倒数是 −2．
2. D【解析】棱柱无论怎么截，截面都不可能有弧度，自然不可能是圆，
故选：D．
3. D【解析】A、抽查对象不具有代表性，故A错误；
B、调查对象不具广泛性、代表性，故B错误；
C、调查对象不具广泛性，故C错误；
D、随机调查本校每个年级 10% 的学生进行调查，故D正确．
4. D【解析】根据题意得：9−−2−1=10，则某人乘电梯从地下 2 层升至地上 9 层，电梯一共升了 10 层，故选：D．
5. C
【解析】若 x=y，则：① x+2=y+2，正确；② −2x−1=−2y−1，正确；③当 a=0 时，xa=ya 不能成立，错误．
6. B【解析】扇形 AOB 的面积 =120⋅π⋅12360=π3．
7. A【解析】2017 年教育方面支出所占的百分比：1−30%−25%−15%=30%，
教育方面支出的金额：1.8×30%=0.54（万元）；
2018 年教育方面支出的金额：2.16×35%=0.756（万元），
小刚家 2018 年教育方面支出的金额比 2017 年增加了 0.756−0.54=0.216（万元）．
8. B【解析】设小强第一次追上小彬的时间为 x 秒，
根据题意，得：6x−4x+115=2×115+2×85，
解得 x=142.5，
则 4x=570，570−400=170>115，
所以他们的位置在直跑道 BC 上，
故选：B．
第二部分
9. 0
10. 普查
11. 2
【解析】根据题意得：
1−8x+9x−3=0,
移项合并得：
x=2,
故答案为：2．
12. 5
【解析】由俯视图易得最底层小立方块的个数为 4，由其他视图可知第二层有一个小立方块，那么共有 4+1=5 个小立方块．
故答案为：5．
13. 6
【解析】∵ 这组数据的极差为 98−46=52，
∴ 若以 10 分为组距分组，共可分 52÷10=5.2≈6（组）．
14. 115
【解析】当时钟指向上午 10:10 时，时针与分针相距 8+1060=496 份，
当时钟指向上午 10:10 时，时针与分针的夹角 30∘×496=245∘，
即当时钟指向上午 10:10 时，时针与分针的夹角 115∘．
15. π422×39=π82210−x
【解析】第一个容器中水的体积为 π422×39；
第二个容器中水的体积为 π82210−x，
∵ 水的体积不变，
∴π422×39=π82210−x．
16. 8
【解析】设原来的两位数为 10a+b，
根据题意得：10a+b+9=10b+a，解得：b=a+1，
∵ 可取 1 到 8 个数，
∴ 这两位数共有 8 个，
它们分别是 12，23，34，45，56，67，78，89．
第三部分
17. 如图，AB 为所作．
18. （1） 原式=−5+115÷−115=−5−1=−6,
（2） 原式=−94×827−13=−23−13=−1,
（3） 原式=−2ab+6a2+5ab−a2=5a2+3ab,
（4） 去分母得：
3x−7−45x+8=12.
去括号得：
3x−21−20x−32=12.
移项得：
3x−20x=12+32+21.
合并同类项得：
−17x=65.
系数化为 1 得：
x=−6517.
19. （1） ∠AOC=∠BOD，理由：
∵∠AOB 和 ∠COD 都是直角，
∴∠AOB=∠COD=90∘，
∴∠AOB+∠AOD=∠COD+∠AOD，即 ∠AOC=∠BOD．
（2） ∵∠BOC=130∘，∠AOB=∠COD=90∘，
∴∠AOD=360∘−∠BOC−∠AOB−∠COD=360∘−130∘−90∘−90∘=50∘,
∵ 射线 OE 是 ∠AOD 的角平分线，
∴∠DOE=12×50∘=25∘．
20. （1） 132
【解析】由题意：BA1=12，BA2=122，BA3=123，⋯BA5=125=132．
（2） 12n
【解析】由（1）可知 BAn=12n．
（3） AA1+A1A2+A2A3+⋯+A7A8=AB−BA8=1−128=255256．
21. （1） x20−2x12−2x
【解析】∵ 它的四个角都剪去一个边长为 x cm 的小正方形，然后把它折成一个无盖的长方体盒子，
∴ 长为 20−2x，宽为 12−2x，高为 x，
∴V=x20−2x12−2x；
故答案为：x20−2x12−2x．
（2） 表中填：当 x=2 时，V=220−412−4=256；
当 x=5 时，V=520−1012−10=100；
故答案为：256；100；
当 x 取 2 时，长方体盒子的容积最大．
（3） 当从正面看长方体，形状是正方形时，x=20−2x 解得 x=203，
当时 x=203，12−2x=−43<0．
所以，不可能是正方形．
22. （1） 因为不及格的频数为 1，频率为 0.05，
所以总人数为 1÷0.05=20 人，
所以良好的频数为 20−1−2−8=9，
优秀的频率为 8÷20=0.40，
故答案为：9，0.40；
统计图补全为：
（2） 0.45×360∘=162∘．
答：“良好”所对应扇形的圆心角为 162∘；
（3） 300×0.45+0.40=255，
答：估计该校本次监测成绩 70 分及以上的学生总共约有 255 人．
23. （1） 设甲购进了 x 件，则乙购进了 100−x 件，
由题意，得：
18x+10100−x=1400,
解得：
x=50,100−x=50
，
答：甲，乙两种商品各购进了 50 件；
（2） 设两种商品的标价总共 y 元．
由题意，得：
18+10×1+10%=0.8y,
解得：
y=38.5,
答：两种商品的标价总共 38.5 元．
24. （1） 探究三：当 a−b=±2 时，
① a−b=2，则 a=b+2，
由已知得：b+2+b=10，
解得：b=4，
∴a=b+2=6，
则 ab=24；
② a−b=−2，即 b−a=2，
由①可得：b=6，a=4，
则 ab=24．
（2） 25；m24；9．
【解析】
a−b⋯−3−2−10123⋯ab⋯914249942599424914⋯