2018-2019学年广东省佛山市禅城区七下期末数学试卷

这是一份2018-2019学年广东省佛山市禅城区七下期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 计算 −32 的结果是
A. 9B. −9C. 6D. −6

2. 下面计算正确的是
A. a33=a5B. a3+a3=a6C. a⋅a2=a3D. al0÷a2=a5

3. 有下列长度的三条线段，能组成三角形的是
A. 2 cm，3 cm，4 cmB. 1 cm，4 cm，2 cm
C. 1 cm，2 cm，3 cmD. 6 cm，2 cm，3 cm

4. 甲骨文是我国古代的一种文字，是汉字的早期形式，反映了我国悠久的历史文化，体现了我国古代劳动人民的智慧，下列甲骨文中，不是轴对称图形的是
A. B.
C. D.

5. 转动下列各转盘，指针指向红色区域的可能性最大的是
A. B.
C. D.

6. 如图，现要从村庄 A 修建一条连接公路 PQ 的最短小路，过点 A 作 AH⊥PQ 于点 H，沿 AH 修建公路，这样做的理由是
A. 两点之间，线段最短B. 垂线段最短
C. 过一点可以作无数条直线D. 两点确定一条直线

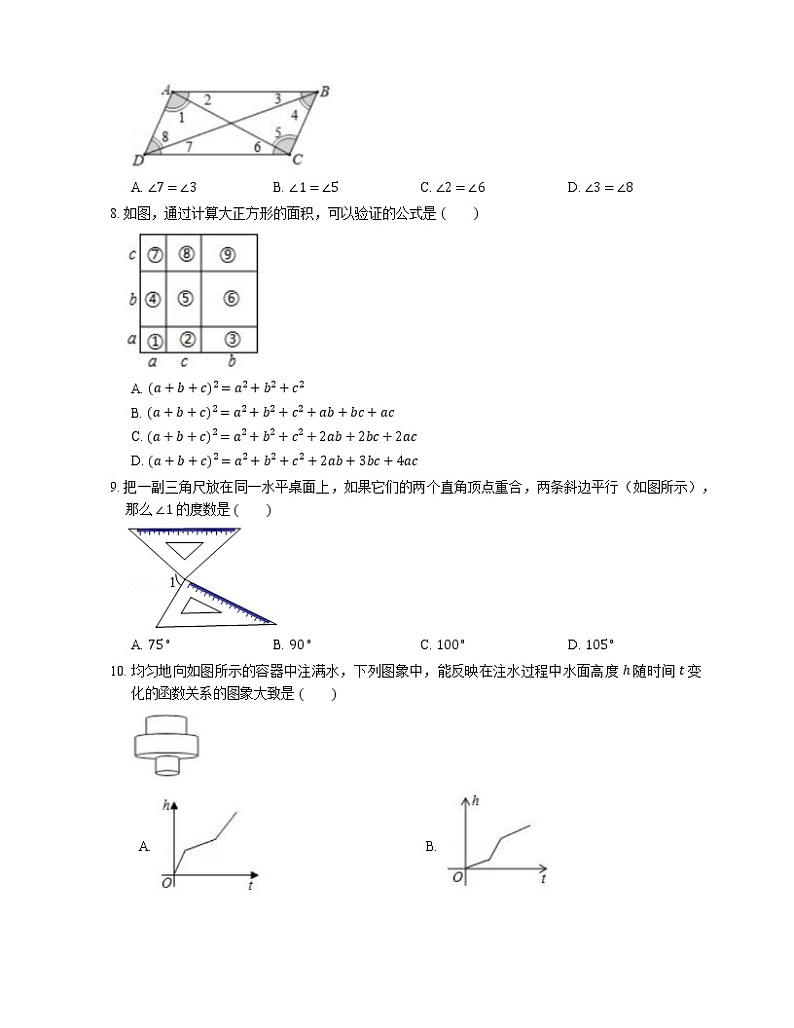
7. 如图，能够判断 AD∥BC 的条件是
A. ∠7=∠3B. ∠1=∠5C. ∠2=∠6D. ∠3=∠8

8. 如图，通过计算大正方形的面积，可以验证的公式是
A. a+b+c2=a2+b2+c2
B. a+b+c2=a2+b2+c2+ab+bc+ac
C. a+b+c2=a2+b2+c2+2ab+2bc+2ac
D. a+b+c2=a2+b2+c2+2ab+3bc+4ac

9. 把一副三角尺放在同一水平桌面上，如果它们的两个直角顶点重合，两条斜边平行（如图所示），那么 ∠1 的度数是
A. 75∘B. 90∘C. 100∘D. 105∘

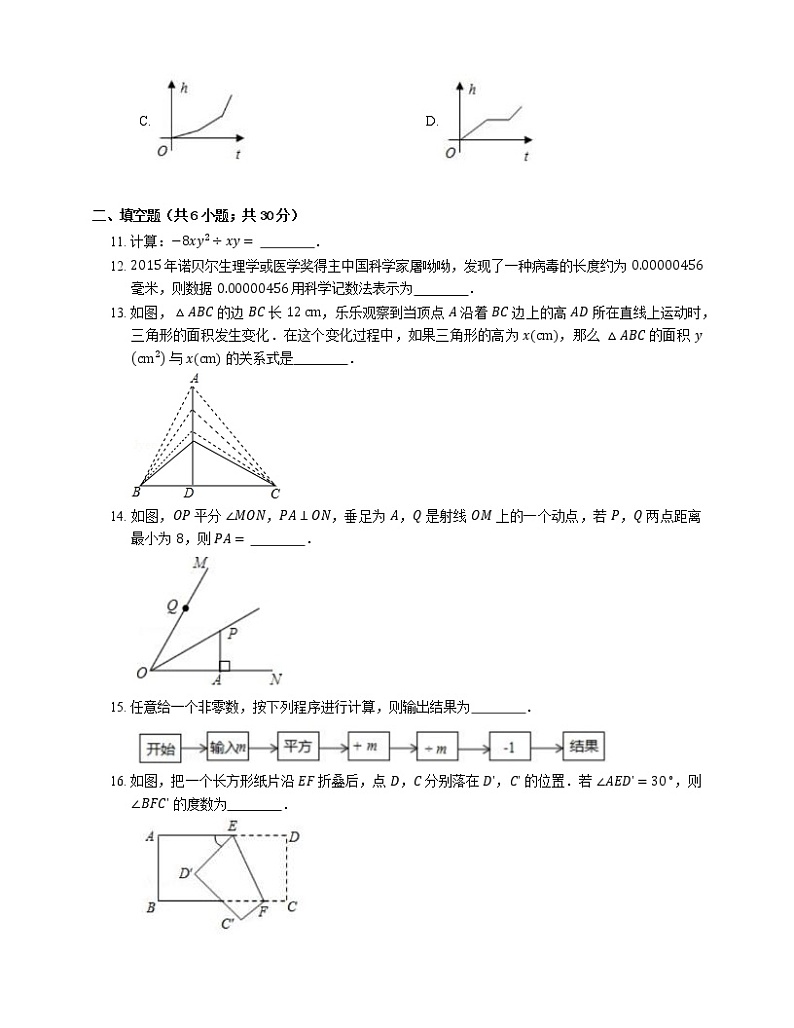
10. 均匀地向如图所示的容器中注满水，下列图象中，能反映在注水过程中水面高度 h 随时间 t 变化的函数关系的图象大致是
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 计算：−8xy2÷xy= ．

12. 2015 年诺贝尔生理学或医学奖得主中国科学家屠呦呦，发现了一种病毒的长度约为 0.00000456 毫米，则数据 0.00000456 用科学记数法表示为 ．

13. 如图，△ABC 的边 BC 长 12 cm，乐乐观察到当顶点 A 沿着 BC 边上的高 AD 所在直线上运动时，三角形的面积发生变化．在这个变化过程中，如果三角形的高为 xcm，那么 △ABC 的面积 ycm2 与 xcm 的关系式是 ．

14. 如图，OP 平分 ∠MON，PA⊥ON，垂足为 A，Q 是射线 OM 上的一个动点，若 P，Q 两点距离最小为 8，则 PA= ．

15. 任意给一个非零数，按下列程序进行计算，则输出结果为 ．

16. 如图，把一个长方形纸片沿 EF 折叠后，点 D，C 分别落在 Dʹ，Cʹ 的位置．若 ∠AEDʹ=30∘，则 ∠BFCʹ 的度数为 ．

三、解答题（共9小题；共117分）
17. 计算：−12+12−1−5÷2019−π0．

18. 如图，AB 和 CD 相交于点 O，∠C=∠COA，OB=BD．求证：AC∥BD．

19. 在一个不透明的盒子里装有红、黑两种颜色的球共 60 只，这些球除颜色外其余完全相同．为了估计红球和黑球的个数，七（4）班的数学学习小组做了摸球实验．他们将球搅匀后，从盒子里随机摸出一个球记下颜色，再把球放回盒子中，多次重复上述过程，得到下表中的一组统计数据：
摸球的次数n5010030050080010002000摸到红球的次数m143395155241298602摸到红球的频率
（1）请估计：当次数 n 足够大时，摸到红球的频率将会接近 ；（精确到 0.1）
（2）假如你去摸一次，则摸到红球的概率的估计值为 ；
（3）试估算盒子里红球的数量为 个，黑球的数量为 个．

20. 先化简，再求值：x−2y2+x−2y2y+x−2x2x−y，其中 x=2，y=12．

21. 把两个同样大小的含 30 度的三角尺像如图所示那样放置，其中 M 是 AD 与 BC 的交点．
（1）求 ∠AMC 的度数；
（2）此时 MC 的长度等于点 M 到 AB 的距离，请说明理由．

22. 已知 △ABC 中，∠A=80∘，∠B=40∘．
（1）尺规作图：在 AB 边上找一点 D 使得 DB=DC（要求：不写作法，保留作图痕迹）；
（2）求 ∠ADC．

23. 生活中处处有数学．
（1）如图（1）所示，一扇窗户打开后，用窗钩 AB 将其固定，这里所运用的数学原理是 ；
（2）如图（2）所示，在新修的小区中，有一条“Z”字形绿色长廊 ABCD，其中 AB∥CD，在 AB，BC，CD 三段绿色长廊上各修一小凉亭 E，M，F，且 BE=CF，点 M 是 BC 的中点，在凉亭 M 与 F 之间有一池塘，不能直接到达，要想知道 M 与 F 之间的距离，只需要测出线段 ME 的长度，这样做合适吗?请说明理由．

24. 如图所示 V球=43πr3．
（1）三个大小相同的球恰好放在一个圆柱形盒子里，三个球的体积占整个盒子容积的 （几分之几）；
（2）若 4 个大小相同的球恰好放在一个圆柱形盒子里，4 个球的体积占整个盒子容积的 （几分之几）；
（3）m 个大小相同的球恰好放在一个圆柱形盒子里，m 个球的体积占整个盒子容积的 （几分之几）．

25. 如图 1，在长方形 ABCD 中，AB=12 cm，BC=10 cm，点 P 从 A 出发，沿 A→B→C→D 的路线运动，到 D 停止；点 Q 从 D 点出发，沿 D→C→B→A 路线运动，到 A 点停止．若 P，Q 两点同时出发，速度分别为每秒 1 cm，2 cm，a 秒时 P，Q 两点同时改变速度，分别变为每秒 2 cm，54 cm（P，Q 两点速度改变后一直保持此速度，直到停止），如图 2 是 △APD 的面积 s（cm2）和运动时间 x（秒）的图象．
（1）求出 a 值；
（2）设点 P 已行的路程为 y1（cm），点 Q 还剩的路程为 y2（cm），请分别求出改变速度后，y1，y2 和运动时间 x（秒）的关系式；
（3）求 P，Q 两点都在 BC 边上，x 为何值时 P，Q 两点相距 3 cm?
答案
第一部分
1. B【解析】−32=−9．
2. C【解析】A．a33=a9，故本选项不合题意；
B．a3+a3=2a3，故本选项不合题意；
C．a⋅a2=a3，故本选项符合题意；
D．al0÷a2=a8 故本选项不合题意．
3. A【解析】根据三角形任意两边的和大于第三边，得
A中，3+2>4，能组成三角形；
B中，1+2<4，不能组成三角形；
C中，1+2=3，不能够组成三角形；
D中，2+3<6，不能组成三角形．
4. D【解析】A、是轴对称图形，故此选项不合题意；
B、是轴对称图形，故此选项不合题意；
C、是轴对称图形，故此选项不合题意；
D、不是轴对称图形，故此选项符合题意；
故选：D．
5. D
【解析】红色区域面积与圆的面积之比即为指针指向红色区域的概率，
观察可知红色区域面积D > C > A > B．
6. B【解析】∵ 从直线外一点到这条直线上各点所连线段中，垂线段最短，
∴ 过点 A 作 AH⊥PQ 于点 H，这样做的理由是垂线段最短．
7. B【解析】A、根据“∠7=∠3”只能判定“DC∥AB”，而非 AD∥BC，故A错误；
B、因为 ∠1=∠5，所以 AD∥BC（内错角相等，两直线平行），故B正确；
C、根据“∠2=∠6”只能判定“DC∥AB”，而非 AD∥BC，故C错误；
D、根据“∠3=∠8”不能判定 AD∥BC，故D错误．
故选：B．
8. C【解析】如图所示：a+b+c2=a2+b2+c2+2ab+2bc+2ac．
9. D【解析】如图：过 ∠1 的顶点作斜边的平行线，
利用平行线的性质可得，∠1=60∘+45∘=105∘．
10. A
【解析】最下面的容器较细，第二个容器最粗，
那么第二个阶段的函数图象水面高度 h 随时间 t 的增大而增长缓慢，用时较长，
最上面容器最大，那么用时最长．
第二部分
11. −4y
【解析】原式=−4y．
12. 4.56×10−6
【解析】0.00000456=4.56×10−6．
13. y=6x
【解析】∵△ABC 的面积 =12BC⋅x=12×12⋅x=6x，
∴y 与 x 的关系式为：y=6x．
14. 8
【解析】过点 P 作 PQ⊥OM，垂足为 Q，则 PQ 长为 P，Q 两点最短距离，
因为 OP 平分 ∠MON，PA⊥ON，PQ⊥OM，
所以 PA=PQ=8．
15. m
【解析】由题意可知：m2+m÷m−1=m+1−1=m，故答案为：m．
16. 30∘
【解析】如图，由翻折得：∠DEF=∠DʹEF，
∴∠AEDʹ=30∘，
∴∠DEF=75∘，
∵ 四边形 ABCD 是长方形纸片，
∴AE∥BC，
∴∠EFB=∠DEF=75∘，
∴∠EFC=180∘−75∘=105∘，
根据翻折不变性，∠EFC=∠EFCʹ=105∘，
∴∠BFCʹ=105∘−75∘=30∘．
第三部分
17. 原式=1+2−5÷1=1+2−5=−2.
18. ∵OB=BD，
∴∠D=∠BOD，
∵∠C=∠COA，∠COA=∠BOD（对顶角相等），
∴∠C=∠D．
∴AC∥BD（内错角相等，两直线平行）．
19. （1） 0.3
（2） 0.3
（3） 18；42
【解析】估算盒子里红球的数量为 60×0.3=18 个，黑球的个数为 60−18=42 个．
20. 原式=x2−4xy+4y2+x2−4y2−4x2+2xy=−2x2−2xy.
当 x=2，y=12 时，
原式=−2×4−2×2×12−8−2=−10.
21. （1） 由题意可得，∠MAB=∠MBA=30∘，
故 ∠AMC=∠MAB+∠MBA=60∘，
即 ∠AMC 的度数是 60∘．
（2） 由题意可知，∠CAB=60∘，∠C=90∘，
所以 ∠MAB=30∘，
所以 ∠MAC=30∘，
所以 AM 平分 ∠CAB，
所以 MC 的长度等于点 M 到 AB 的距离．
22. （1） 如图所示：D 点为所求．
（2） ∵∠A=80∘，∠B=40∘，
∴∠ACB=60∘，
又 DB=DC，∠B=40∘，
∴∠DCB=∠B=40∘，
∴∠ACD=∠ACB−∠DCB=20∘．
23. （1） 三角形具有稳定性
【解析】如图 1 所示，一扇窗户打开后，用窗钩 AB 可将其固定，这里所运用的几何原理是：三角形的稳定性．
（2） 合适，理由如下：
∵AB∥CD，
∴∠B=∠C，
∵ 点 M 是 BC 的中点，
∴MB=MC，
在 △MEB 与 △MCF 中，BE=CF,∠B=∠C,BM=MC,
∴△MEB≌△MFCSAS，
∴ME=MF，
∴ 想知道 M 与 F 之间的距离，只需要测出线段 ME 的长度．
24. （1） 23
【解析】设球的半径为 r．
根据题意得：三个球的体积之和 =3×43πr3=4πr3，
圆柱体盒子容积 =πr2⋅6r=6πr3，
∴4πr36πr3=23．
即三个球的体积之和占整个盒子容积的 23．
（2） 23
【解析】设球的半径为 r，
根据题意得：四个球的体积之和 =4×43πr3=163πr3，
圆柱体盒子容积 =πr2⋅8r=8πr3，
∴163πr38πr3=23．
即四个球的体积之和占整个盒子容积的 23．
（3） 23
【解析】设球的半径为 r．
根据题意得：m 个球的体积之和 =43πr3=4m3πr3，
圆柱体盒子容积 =πr2⋅2mr=2mπr3，
∴4m3πr32mπr3=23，即 m 个球的体积之和占整个盒子容积的 23．
25. （1） 由图象可知，当点 P 在 BC 上运动时，△APD 的面积保持不变，则 a 秒时，点 P 在 AB 上．
12×10AP=30，
所以 AP=6，
则 a=6．
（2） 由（1）6 秒后点 P 变速，则点 P 已行的路程为 y1=6+2x−6=2x−6，
因为 Q 点路程总长为 34 cm，第 6 秒时已经走 12 cm，点 Q 还剩的路程为 y2=34−12−54x−6=592−54x．
（3） 当 P，Q 两点相遇前相距 3 cm 时，
592−54x−2x−6=3，
解得 x=10，
当 P，Q 两点相遇后相距 3 cm 时，
2x−6−592−54x=3，
解得 x=15413，
所以当 x=10或15413 时，P，Q 两点相距 3 cm．