

2018-2019学年广东广州市天河区广州中学八下期末数学试卷
展开一、选择题(共10小题;共50分)
1. 下列二次根式中,属于最简二次根式的是
A. 25B. 7C. 13D. 12
2. 以下列各组数据为边长作三角形,其中能组成直角三角形的是( )
A. 5,12,13B. 3,5,27C. 6,9,14D. 4,10,13
3. 若一组数据1,4,7,x,5的平均数为4,则x的值时( )
A. 7B. 5C. 4D. 3
4. 函数 y=−x−3 的图象不经过
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
5. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数 x 与方差 S2:
甲乙丙丁平均数xcm175173175174方差
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择
A. 甲B. 乙C. 丙D. 丁
6. 下列命题中,真命题是
A. 有两边相等的平行四边形是菱形
B. 有一个角是直角的四边形是矩形
C. 四个角相等的菱形是正方形
D. 两条对角线互相垂直且相等的四边形是正方形
7. 已知正比例函数 y=kx ,且 y 随 x 的增大而减少,则直线 y=2x+k 的图象是
A. B.
C. D.
8. 如图所示,矩形纸片 ABCD 中,已知 AD=8,折叠纸片使 AB 边与对角线 AC 重合,点 B 落在点 F 处,折痕为 AE,且 EF=3,则 AB 的长为
A. 3B. 4C. 5D. 6
9. 如图,过平行四边形 ABCD 对角线交点 O 的线段 EF,分别交 AD,BC 于点 E,F,当 AE=ED 时,△AOE 的面积为 4,则四边形 EFCD 的面积是
A. 8B. 12C. 16D. 32
10. 如图,在平面直角坐标系中,点 A1,A2,A3 在直线 y=15x+b 上,点 B1,B2,B3 在 x 轴上,△OA1B1,△B1A2B2,△B2A3B3 都是等腰直角三角形,若已知点 A11,1,则点 A3 的纵坐标是
A. 32B. 23C. 49D. 94
二、填空题(共6小题;共30分)
11. 若式子 x+x−1 在实数范围内有意义,则 x 的取值范围是 .
12. 若一直角三角形的两直角边长为 3,1,则斜边长为 .
13. 把直线 y=−x−1 沿着 y 轴向上平移 2 个单位,所得直线的函数解析式为 y= .
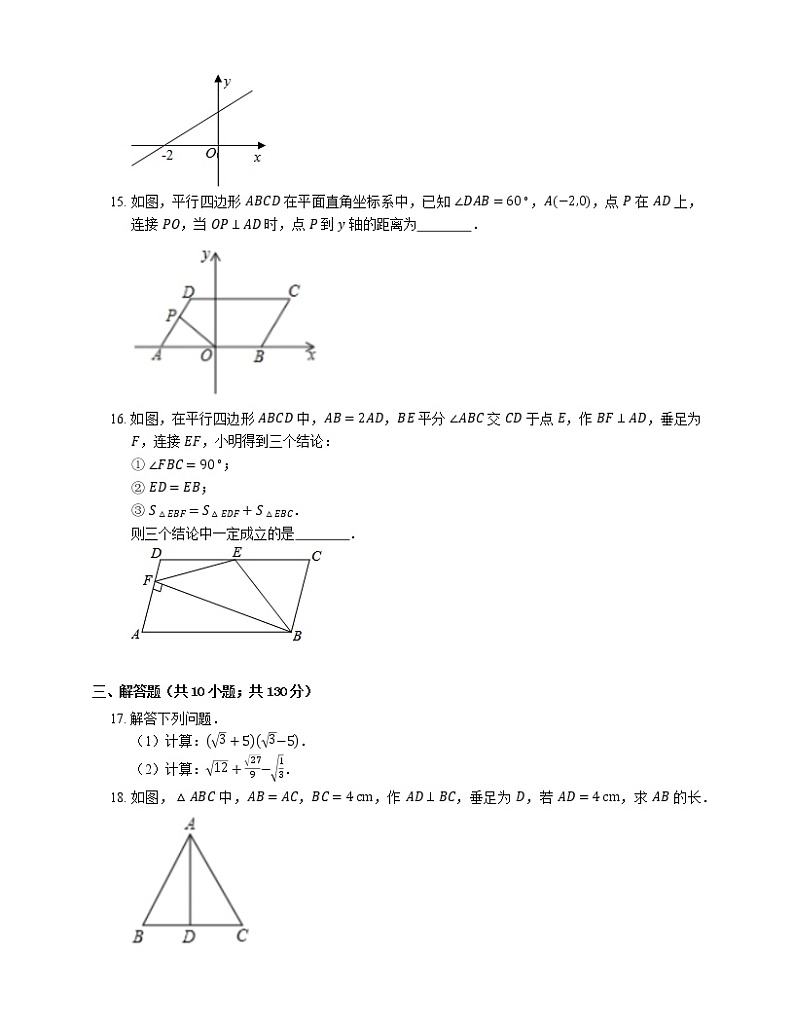
14. 如图,直线 y=kx+bk>0 与 x 轴的交点为 −2,0,则关于 x 的不等式 kx+b<0 的解集是 .
15. 如图,平行四边形 ABCD 在平面直角坐标系中,已知 ∠DAB=60∘,A−2,0,点 P 在 AD 上,连接 PO,当 OP⊥AD 时,点 P 到 y 轴的距离为 .
16. 如图,在平行四边形 ABCD 中,AB=2AD,BE 平分 ∠ABC 交 CD 于点 E,作 BF⊥AD,垂足为 F,连接 EF,小明得到三个结论:
① ∠FBC=90∘;
② ED=EB;
③ S△EBF=S△EDF+S△EBC.
则三个结论中一定成立的是 .
三、解答题(共10小题;共130分)
17. 解答下列问题.
(1)计算:3+53−5.
(2)计算:12+279−13.
18. 如图,△ABC 中,AB=AC,BC=4 cm,作 AD⊥BC,垂足为 D,若 AD=4 cm,求 AB 的长.
19. 如图,已知平行四边形 ABCD 的对角线 AC 和 BD 交于点 O,且 AC+BD=28,BC=12,求 △AOD 的周长.
20. 某校八年级学生在一次射击训练中,随机抽取 10 名学生的成绩如下表,请回答问题:
环数6789人数152
(1)填空:10 名学生的射击成绩的众数是 ,中位数是 .
(2)求这 10 名学生的平均成绩.
(3)若 9 环(含 9 环)以上评为优秀射手,试估计全年级 500 名学生中有多少是优秀射手?
21. 如图,△ABC 是等边三角形.
(1)利用直尺和圆规按要求完成作图(保留作图痕迹);
① 作线段 AC 的中点 M.
② 连接 BM,并延长到 D,使 MD=MB,连接 AD,CD.
(2)求证(1)中所作的四边形 ABCD 是菱形.
22. 在平面直角坐标系中,原点为 O,已知一次函数的图象过点 A0,5,点 B−1,4 和点 Pm,n.
(1)求这个一次函数的解析式;
(2)当 n=2 时,求直线 AB,直线 OP 与 x 轴围成的图形的面积;
(3)当 △OAP 的面积等于 △OAB 的面积的 2 倍时,求 n 的值.
23. 如图,菱形 ABCD 的对角线 AC 和 BD 相交于点 O,AB=5,OA=a,OB=b,且 a,b 满足:a2+b2a2b2=54.
(1)求菱形 ABCD 的面积;
(2)求 a+bab 的值.
24. 如图,在平面直角坐标系中,O 为原点,点 A2,1,B−2,4,直线 AB 与 y 轴交于点 C.
(1)求点 C 的坐标;
(2)求证:△OAB 是直角三角形.
25. 如图,矩形 ABCD 中,OB=5,OD=3,以 O 为原点建立平面直角坐标系,点 B,点 D 分别在 x 轴,y 轴上,点 C 在第一象限内,若平面内有一动点 P,且满足 S△POB=13S矩形OBCD,问:
(1)当点 P 在矩形的对角线 OC 上,求点 P 的坐标;
(2)当点 P 到 O,B 两点的距离之和 PO+PB 取最小值时,求点 P 的坐标.
26. 如图,在菱形 ABCD 中,∠A=60∘,AD=8,F 是 AB 的中点,过点 F 作 FE⊥AD,垂足为 E,将 △AEF 沿点 A 到点 B 的方向平移,得到 △AʹEʹFʹ.
(1)求 EF 的长;
(2)设 P,Pʹ 分别是 EF,EʹFʹ 的中点,当点 Aʹ 与点 B 重合时,求证四边形 PPʹCD 是平行四边形,并求出四边形 PPʹCD 的面积.
答案
第一部分
1. B【解析】A.25=5,故此选项错误;
B.7 是最简二次根式,故此选项正确;
C.13=33,故此选项错误;
D.12=23,故此选项错误.
2. A【解析】【分析】先分别求出两个小边的平方和,再求出最长边的平方,看看是否相等即可.
【解析】解:A、52+122=132,即以5、12、13为边能组成直角三角形,故本选项符合题意;
B、32+52≠(27)2,即以3、5、27为边不能组成直角三角形,故本选项不符合题意;
C、62+92≠142,即以6、9、14为边不能组成直角三角形,故本选项不符合题意;
D、42+102≠132,即以4、10、13为边不能组成直角三角形,故本选项不符合题意;
故选:A.
【点评】本题考查了勾股定理的逆定理,能熟记勾股定理的逆定理的内容是解此题的关键.
3. D【解析】【分析】运用平均数的计算公式即可求得x的值.
【解析】解:依题意有:1+4+7+x+5=4×5,
解得x=3.
故选:D.
【点评】本题考查的是样本平均数的求法及运用,关键是熟练掌握平均数公式.
4. A【解析】∵k=−1<0,
∴ 一次函数经过二四象限;
∵b=−3<0,
∴ 一次函数又经过第三象限,
∴ 一次函数 y=−x−3 的图象不经过第一象限.
5. A
6. C【解析】A、两邻边相等的平行四边形是菱形,所以A选项错误;
B、有一个角是直角的平行四边形是矩形,所以B选项错误;
C、四个角相等的菱形是正方形,所以C选项正确;
D、两条对角线互相垂直平分且相等的四边形是正方形,所以D选项错误.
7. D【解析】∵ 正比例函数 y=kx ,且 y 随 x 的增大而减少,
∴k<0 .
在直线 y=2x+k 中,
∵2>0 , k<0 ,
∴ 函数图象经过一三四象限.
8. D
9. C【解析】∵ABCD 是平行四边形,
∴AD∥BC,AD=BC,AO=CO,OB=OD,
∴∠DAC=∠ACB,
∵∠AOE=∠COF,
∴△COF≌△AOEASA,
∵S△AOE=4,AE=ED,
∴S△COF=S△DOE=S△AOE=4,
∴S△AOD=8,
∵AO=CO,
∴S△COD=S△AOD=8,
∴S四边形EFCD=S△DOE+S△COD+S△COF=4+8+4=16.
10. D
【解析】∵A11,1 在直线 y=15x+b 上,
∴b=45,
∴y=15x+45.
设 A2x2,y2,A3x3,y3,
则有 y2=15x2+45,y3=15x3+45.
又 ∵△OA1B1,△B1A2B2,△B2A3B3 都是等腰直角三角形.
∴x2=2y1+y2,x3=2y1+2y2+y3,
将点坐标依次代入直线解析式得到:y2=12y1+1,y3=12y1+12y2+1=32 y2
又 ∵y1=1
∴y2=32,y3=322=94,
∴ 点 A3 的纵坐标是 94.
第二部分
11. x≥1
【解析】由题意,得 x−1≥0,解得 x≥1.
12. 2
【解析】斜边长 =32+12=2.
13. −x+1
【解析】把直线 y=−x−1 沿着 y 轴向上平移 2 个单位,所得直线的函数解析式为 y=−x−1+2,即 y=−x+1.
14. x<−2
【解析】∵ 直线 y=kx+bk>0 与 x 轴的交点为 −2,0,
∴y 随 x 的增大而增大,当 x<−2 时,y<0,即 kx+b<0.
15. 32
【解析】∵A−2,0,
∴OA=2,
∵∠DAB=60∘,
∴OP=3,
作 PE⊥y 轴,
∵∠POA=30∘,
∴∠OPE=30∘,
∴PE=PO×cs30∘=32,
∴ 点 P 到 y 轴的距离为 32.
16. ①③
【解析】∵BF⊥AD,
∴∠AFB=90∘,
∵ 在平行四边形 ABCD 中,AD∥BC,
∴∠AFB=∠CBF=90∘,故①正确;
延长 FE 交 BC 的延长线于 M,
∴∠DFE=∠M,
在 △DFE 与 △CME 中,
∠DFE=∠M,∠DEF=∠CEM,DE=CE,
∴△DFE≌△CMEAAS,
∴EF=EM=12FM,
∵∠FBM=90∘,
∴BE=12FM,
∴EF=BE,
∵EF≠DE,
故②错误;
∵EF=EM,
∴S△BEF=S△BME,
∵△DFE≌△CME,
∴S△DFE=S△CME,
∴S△EBF=S△BME=S△EDF+S△EBC,故③正确.
第三部分
17. (1) 原式=3−25=−22.
(2) 原式=23+33−33=23.
18. ∵AB=AC,BC=4 cm,AD⊥BC,
∴BD=12BC=4,
∵AD=4 cm,
∴AB=AD2+BD2=25.
19. ∵ 四边形 ABCD 是平行四边形,
∴AO=CO,BO=DO,
∵AC+BD=28,
∴AO+OD=14,
∵AD=BC=12,
∴△AOD 的周长 =AO+OD+AD=14+12=26.
20. (1) 7 环;7 环
【解析】射击成绩出现次数最多的是 7 环,共出现 5 次,因此众数是 7 环,射击成绩从小到大排列后处在第 5,6 位的数都是 7 环,因此中位数是 7 环.
(2) 6+7×5+8×2+9×210=7.5 环,
答:这 10 名学生的平均成绩为 7.5 环.
(3) 500×210=100 人,
答:全年级 500 名学生中有 100 名是优秀射手.
21. (1) 如图,四边形 ABCD 即为所求.
(2) ∵AM=MC,BM=MD,
∴ 四边形 ABCD 是平行四边形,
∵△ABC 是等边三角形,AM=MC,
∴BD⊥AC,
∴ 四边形 ABCD 是菱形.
22. (1) 设这个一次函数的解析式是 y=kx+b,
把点 A0,5,点 B−1,4 的坐标代入得:b=5,−k+b=4,
解得:k=1,b=5,
∴ 这个一次函数的解析式是 y=x+5.
(2) 设直线 AB 交 x 轴于 C,如图.
当 y=0 时,x+5=0,解得 x=−5,则 C−5,0;
当 n=2 时,S△OPC=12×5×2=5,
即直线 AB,直线 OP 与 x 轴围成的图形的面积为 5.
(3) ∵ 当 △OAP 的面积等于 △OAB 的面积的 2 倍,
∴12×5×m=2×12×1×5,
∴m=2 或 m=−2,即 P 点的横坐标为 2 或 −2.
当 x=2 时,y=x+5=7,此时 P2,7;
当 x=−2 时,y=x+5=3,此时 P−2,3.
综上所述,n 的值为 7 或 3.
23. (1) ∵ 四边形 ABCD 是菱形,
∴BD 垂直平分 AC,
∵OA=a,OB=b,AB=5,
∴a2+b2=5,
∵a,b 满足:a2+b2a2b2=54.
∴a2b2=4,
∴ab=2,
∴△AOB 的面积 =12ab=1,
∴ 菱形 ABCD 的面积 =4△AOB 的面积 =4.
(2) ∵a2+b2=5,ab=2,
∴a+b2=a2+b2+2ab=7,
∴a+b=7,
∴a+bab=72.
24. (1) 设直线 AB 的解析式为:y=kx+b,
点 A2,1,B−2,4,
则 2k+b=1,−2k+b=4, 解得,k=−34,b=52,
∴ 设直线 AB 的解析式为:y=−34x+52,
∴ 点 C 的坐标为 0,52.
(2) ∵ 点 A2,1,B−2,4,
∴OA2=22+12=5,OB2=22+42=20,AB2=32+42=25,
则 OA2+OB2=AB2,
∴△OAB 是直角三角形.
25. (1) ∵ 矩形 ABCD 中,OB=5,OD=3,
∴C5,3,设直线 OC 的解析式为 y=kx,
∴3=5k,
∴k=35,
∴ 直线 OC 的解析式为 y=35x,
∵ 点 P 在矩形的对角线 OC 上,
∴ 设 Pm,35m,
∵S△POB=13S矩形OBCD,
∴12×5×35m=13×3×5,
∴m=103,
∴P103,2.
(2) ∵S△POB=13S矩形OBCD,
∴ 设点 P 的纵坐标为 h,
∴12h×5=13×3×5,
∴h=2,
∴ 点 P 在直线 y=2 或 y=−2 的直线上,
作 B 关于直线 y=2 的对称点 E,则点 E 的坐标为 5,4,连接 OE 交直线 y=2 于 P,则此时 PO+PB 的值最小,
设直线 OE 的解析式为 y=nx,
∴4=5n,
∴n=45,
∴ 直线 OE 的解析式为 y=45x,
当 y=2 时,x=85,
∴P85,2,
同理,点 P 在直线 y=−2 的直线上,P85,−2,
∴ 点 P 的坐标为 85,2 或 −85,2.
26. (1) ∵ 四边形 ABCD 是菱形,
∴AD=AB=8,
∵F 是 AB 的中点,
∴AF=12AB=12×8=4,
∵ 点 F 作 FE⊥AD,∠A=60∘,
∴EF=sin60∘×4=23.
(2) 如图,连接 BD,DF,DF 交 PPʹ 于 H.
由题意 PPʹ=AAʹ=AB=CD,PPʹ∥AAʹ∥CD,
∴ 四边形 PPʹCD 是平行四边形,
∵ 四边形 ABCD 是菱形,∠A=60∘,
∴△ABD 是等边三角形,
∵AF=FB,
∴DF⊥AB,DF⊥PPʹ,
在 Rt△AEF 中,
∵∠AEF=90∘,∠A=60∘,AF=4,
∴AE=2,EF=23,
∴PE=PF=3,
在 Rt△PHF 中,
∵∠FPH=30∘,PF=3,
∴HF=12PF=32,
∵DF=43,
∴DH=43−32=732,
∴ 平行四边形 PPʹCD 的面积 =732×8=283.
2018-2019学年广东省广州市天河区天河中学八下期中数学试卷: 这是一份2018-2019学年广东省广州市天河区天河中学八下期中数学试卷,共10页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
2018-2019学年广东省广州市天河区广州中学七上期中数学试卷: 这是一份2018-2019学年广东省广州市天河区广州中学七上期中数学试卷,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年广东省广州市天河区广州市第一一三中学九上期中数学试卷: 这是一份2018-2019学年广东省广州市天河区广州市第一一三中学九上期中数学试卷,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












