2020年江苏省无锡市滨湖区中考模拟数学试卷（3月份）

这是一份2020年江苏省无锡市滨湖区中考模拟数学试卷（3月份），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 9 的算术平方根是
A. ±3B. 13C. 3D. −3

2. 下列运算正确的是
A. a3⋅a2=a6B. a7÷a3=a4
C. −3a2=−6a2D. a−12=a2−1

3. 下列各数中，属于无理数的是
A. −2B. 0C. 3D. 0.101001000

4. 函数 y=x−2 的自变量 x 的取值范围是
A. x>2B. x≥2C. x≠2D. x≤2

5. 关于 x 的一元二次方程 x2−4x+m=0 的两实数根分别为 x1，x2，且 x1+3x2=5，则 m 的值为
A. 74B. 75C. 76D. 0

6. 如图，将一块含有 30∘ 的直角三角板的顶点放在直尺的一边上．若 ∠1=48∘，那么 ∠2 的度数是
A. 48∘B. 78∘C. 92∘D. 102∘

7. 若一元二次方程 x2−2kx+k2=0 的一根为 x=−1，则 k 的值为
A. −1B. 0C. 1 或 −1D. 2 或 0

8. 已知直角三角形的外接圆半径为 6，内切圆半径为 2，那么这个三角形的面积是
A. 32B. 34C. 27D. 28

9. 在同一平面直角坐标系中，函数 y=−x+k 与 y=kx（k 为常数，且 k≠0）的图象大致是
A. B.
C. D.

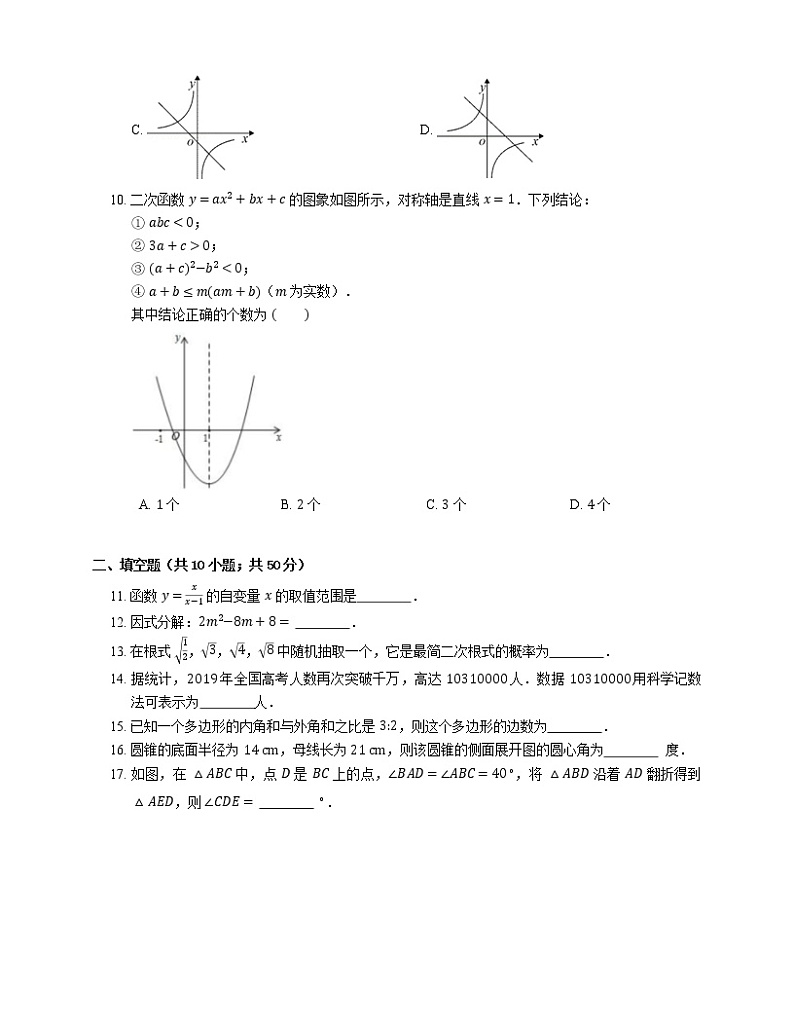
10. 二次函数 y=ax2+bx+c 的图象如图所示，对称轴是直线 x=1．下列结论：
① abc<0；
② 3a+c>0；
③ a+c2−b2<0；
④ a+b≤mam+b（m 为实数）．
其中结论正确的个数为
A. 1 个B. 2 个C. 3 个D. 4 个

二、填空题（共10小题；共50分）
11. 函数 y=xx−1 的自变量 x 的取值范围是 ．

12. 因式分解：2m2−8m+8= ．

13. 在根式 12，3，4，8 中随机抽取一个，它是最简二次根式的概率为 ．

14. 据统计，2019 年全国高考人数再次突破千万，高达 10310000 人．数据 10310000 用科学记数法可表示为 人．

15. 已知一个多边形的内角和与外角和之比是 3:2，则这个多边形的边数为 ．

16. 圆锥的底面半径为 14 cm，母线长为 21 cm，则该圆锥的侧面展开图的圆心角为 度．

17. 如图，在 △ABC 中，点 D 是 BC 上的点，∠BAD=∠ABC=40∘，将 △ABD 沿着 AD 翻折得到 △AED，则 ∠CDE= ∘．

18. 如图，直径 AB 为 6 的半圆，绕 A 点逆时针旋转 60∘，此时点 B 到了点 Bʹ，则图中阴影部分的面积是 ．

19. 如图，正比例函数 y1=k1x 的图象与反比例函数 y2=k2xx>0 的图象相交于点 A3,23，点 B 是反比例函数图象上一点，它的横坐标是 3，连接 OB，AB，则 △AOB 的面积是 ．

20. 如图，正方形 ABCD 的对角线 AC 上有一点 E ，且 CE=4AE ，点 F 在 DC 的延长线上，连接 EF ，过点 E 作 EG⊥EF ，交 CB 的延长线于点 G ，连接 GF 并延长，交 AC 的延长线于点 P ，若 AB=5 ， CF=2 ，则线段 EP 的长是 ．

三、解答题（共8小题；共104分）
21. 解答下列问题．
（1）计算：−32−π−40+12−2；
（2）a+22+1−a1+a．
（3）解方程：32x=1x−1；
（4）解不等式组：12x+1<32,1−5x+1≤6.

22. 化简 1a−b−1a+b÷ab2a2−b2，当 a=3−1，b=3+1 时，求出这个代数式的值．

23. 如图，在 △ABC 中，AB=AC，∠DAC 是 △ABC 的一个外角．实验与操作：根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）
（1）作 ∠DAC 的平分线 AM；
（2）作线段 AC 的垂直平分线，与 AM 交于点 F，与 BC 边交于点 E，连接 AE，CF．探究与猜想：若 ∠BAE=36∘，求 ∠B 的度数．

24. 如图，在 △ABC 中，CD 是 AB 边上的中线，E 是 CD 的中点，过点 C 作 AB 的平行线交 AE 的延长线于点 F，连接 BF．
（1）求证：CF=AD；
（2）若 CA=CB，∠ACB=90∘，试判断四边形 CDBF 的形状，并说明理由．

25. 如图，AB 为 ⊙O 的直径，F 为弦 AC 的中点，连接 OF 并延长交弧 AC 于点 D，过点 D 作 ⊙O 的切线，交 BA 的延长线于点 E．
（1）求证：AC∥DE；
（2）连接 CD，若 OA=AE=2 时，求出四边形 ACDE 的面积．

26. 小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为 8 元/千克，下面是他们在活动结束后的对话．
小丽：如果以 10 元/千克的价格销售，那么每天可售出 300 千克．
小强：如果每千克的利润为 3 元，那么每天可售出 250 千克．
小红：如果以 13 元/千克的价格销售，那么每天可获取利润 750 元．
【利润 =（销售价 − 进价）× 销售量】
（1）请根据他们的对话填写如表：
销售单价x元/kg101113销售量ykg
（2）请你根据表格中的信息判断每天的销售量 y（千克）与销售单价 x（元/kg）之间存在怎样的函数关系．并求 y（千克）与 x（元/kg）（x>0）的函数关系式；
（3）设该超市销售这种水果每天获取的利润为 W 元，求 W 与 x 之间的函数关系式．当销售单价为何值时，每天可获得的利润最大?最大利润是多少元?

27. 如图，在平面直角坐标系中，直线 y=−34x+b 分别与 x 轴，y 轴交于点 A，B，且点 A 的坐标为 4,0，四边形 ABCD 是正方形．
（1）填空：b= ；
（2）求点 D 的坐标；
（3）点 M 是线段 AB 上的一个动点（点 A，B 除外），试探索在 x 上方是否存在另一个点 N，使得以 O，B，M，N 为顶点的四边形是菱形?若不存在，请说明理由；若存在，请求出点 N 的坐标．

28. 已知二次函数 y=ax2+4amxm>0 的对称轴与 x 轴交于点 B，与直线 l:y=−12x 交于点 C，点 A 是该二次函数图象与直线 l 在第二象限的交点，点 D 是抛物线的顶点，已知 AC:CO=1:2，∠DOB=45∘，△ACD 的面积为 2．
（1）求抛物线的函数关系式；
（2）若点 P 为抛物线对称轴上的一个点，且 ∠POC=45∘，求点 P 坐标．
答案
第一部分
1. C【解析】9 的算术平方根是 3．
2. B【解析】A．原式=a5，不符合题意；
B．原式=a4，符合题意；
C．原式=9a2，不符合题意；
D．原式=a2−2a+1，不符合题意．
3. C【解析】∵−2，0 是整数，
∴−2，0 是有理数；
∵0.101001000 是有限小数，
∴0.101001000 是有理数；
∵3=1.732⋯ 是无限不循环小数，
∴3 是无理数．
4. B【解析】根据题意知 x−2≥0，解得：x≥2．
5. A
【解析】∵x1+x2=4，
∴x1+3x2=x1+x2+2x2=4+2x2=5，
∴x2=12，
把 x2=12 代入 x2−4x+m=0 得：122−4×12+m=0，
解得：m=74．
6. D
7. A【解析】把 x=−1 代入方程得：1+2k+k2=0，解得：k=−1．
8. D【解析】如图，点 O 是 △ABC 的外心，点 D 是 △ABC 的内心，E，F，M 是 △ABC 内切圆与 △ABC 的切点．
设 AB=a，BC=b，则有 2=a+b−122，
∴a+b=16，
∴a2+2ab+b2=256，
∵a2+b2=122=144，
∴2ab=112，
∴12ab=28，
∴△ABC 的面积为 28．
9. C【解析】∵ 函数 y=−x+k 与 y=kx（k 为常数，且 k≠0），
∴ 当 k>0 时，y=−x+k 经过第一、二、四象限，y=kx 经过第一、三象限，故选项A，B错误；
当 k<0 时，y=−x+k 经过第二、三、四象限，y=kx 经过第二、四象限，故选项C正确，选项D错误．
10. C
【解析】① ∵ 抛物线开口向上，
∴a>0，
∵ 抛物线的对称轴在 y 轴右侧，
∴b<0，
∵ 抛物线与 y 轴交于负半轴，
∴c<0，
∴abc>0，①错误；
②当 x=−1 时，y>0，
∴a−b+c>0，
∵−b2a=1，
∴b=−2a，
把 b=−2a 代入 a−b+c>0 中得 3a+c>0，
∴ ②正确；
③当 x=1 时，y<0，
∴a+b+c<0，
∴a+c<−b，
∵a>0，c>0，−b>0，
∴a+c2<−b2，即 a+c2−b2<0，
∴ ③正确；
④ ∵ 抛物线的对称轴为直线 x=1，
∴x=1 时，函数的最小值为 a+b+c，
∴a+b+c≤am2+mb+c，
即 a+b≤mam+b，
∴ ④正确．
第二部分
11. x≠1
【解析】由题意得，x−1≠0，解得 x≠1．
12. 2m−22
【解析】2m2−8m+8=2m2−4m+4=2m−22．
13. 14
【解析】∵12，3，4，8 中最简根式只有 3，
∴ 是最简二次根式的概率为 14．
14. 1.031×107
【解析】10310000=1.031×107．
15. 5
【解析】设这个多边形的边数为 n，依题意得：
n−2180∘=32×360∘，
解得 n=5．
故这个多边形的边数为 5．
16. 240
17. 20
【解析】∵∠BAD=∠ABC=40∘，将 △ABD 沿着 AD 翻折得到 △AED，
∴∠ADC=40∘+40∘=80∘，∠ADE=∠ADB=180∘−40∘−40∘=100∘，
∴∠CDE=100∘−80∘=20∘．
18. 6π
【解析】阴影部分的面积 = 以 ABʹ 为直径的半圆的面积 + 扇形 ABBʹ 的面积 − 以 AB 为直径的半圆的面积 = 扇形 ABBʹ 的面积，则阴影部分的面积是：60π×62360=6π．
19. 23
【解析】∵ 正比例函数 y1=k1x 的图象与反比例函数 y2=k2xx>0 的图象相交于点 A3,23，
∴23=3k1，23=k23，
∴k1=2，k2=6，
∴ 正比例函数为 y=2x，反比例函数为：y=6x，
过点 B 作 BD∥x 轴交 OA 于点 D，
∵ 点 B 是反比例函数图象上一点，它的横坐标是 3，
∴y=63=2，
∴B3,2，
∴D1,2，
∴BD=3−1=2．
∴S△AOB=S△ABD+S△OBD=12×2×23−2+12×2×2=23．
20. 1322
【解析】如图，作 FH⊥PE 于 H ．
∵ 四边形 ABCD 是正方形， AB=5 ，
∴AC=52 ， ∠ACD=∠FCH=45∘ ，
∵∠FHC=90∘ ， CF=2 ，
∴CH=HF=2 ，
∵CE=4AE ，
∴EC=42 ， AE=2 ，
∴EH=52 ，
在 Rt△EFH 中， EF2=EH2+FH2=522+22=52 ，
∵∠GEF=∠GCF=90∘ ，
∴E ， G ， F ， C 四点共圆，
∴∠EFG=∠ECG=45∘ ，
∴∠ECF=∠EFP=135∘ ，
∵∠CEF=∠FEP ，
∴△CEF∽△FEP ，
∴EFEP=ECEF ，
∴EF2=EC⋅EP ，
∴EP=5242=1322 ．
故答案为 1322 ．
第三部分
21. （1） 原式=9−1+4=8+4=12.
（2） 原式=a2+4a+4+1−a2=4a+5.
（3） 去分母得：
3x−3=2x.
解得：
x=3.
经检验 x=3 是分式方程的解．
（4）
12x+1<32, ⋯⋯①1−5x+1≤6. ⋯⋯②
由①得：
x<1.
由②得：
x≥−2.
则不等式组的解集为
−2≤x<1.
22. 原式=a+b−a+ba+ba−b⋅a+ba−bab2=2ba+ba−b⋅a+ba−bab2=2ab.
故当 a=3+1，b=3−1 时，
原式=2ab=1.
23. （1） 如图，AM 为所作．
（2） ∵AB=AC，
∴∠B=∠3，
∵AM 平分 ∠DAC，
∴∠1=∠2，
而 ∠DAC=∠B+∠3，
∴∠B=∠2=∠3=∠1，
∴EF 垂直平分 AC，
∴EA=EC，
∴∠3=∠EAC，
∵∠1+∠2+∠EAC+∠BAE=180∘，
∴∠1=13180∘−36∘=48∘，
∴∠B=48∘．
24. （1） ∵CF∥AB，
∴∠CFE=∠DAE，∠FCE=∠ADE，
∵E 为 CD 的中点，
∴CE=DE，
在 △ECF 和 △EDA 中，∠CFE=∠DAE,∠FCE=∠ADE,CE=DE,
∴△ECF≌△EDAAAS，
∴CF=AD．
（2） 四边形 CDBF 为正方形，理由如下：
∵CD 是 AB 边上的中线，
∴AD=BD，
∵CF=AD，
∴CF=BD，
∵CF=BD，CF∥BD，
∴ 四边形 CDBF 为平行四边形，
∵CA=CB，CD 为 AB 边上的中线，
∴CD⊥AB，即 ∠BDC=90∘，
∴ 四边形 CDBF 为矩形，
∵ 等腰直角 △ABC 中，CD 为斜边上的中线，
∴CD=12AB=BD，
∴ 四边形 CDBF 为正方形．
25. （1） ∵F 为弦 AC（非直径）的中点，
∴AF=CF，
∴OD⊥AC，
∵DE 切 ⊙O 于点 D，
∴OD⊥DE，
∴AC∥DE．
（2） ∵AC∥DE，且 OA=AE，
∴F 为 OD 的中点，即 OF=FD，
在 △AFO 和 △CFD 中
OF=FD,∠AFO=∠CFD,AF=CF,
∴△AFO≌△CFDSAS，
∴S△AFO=S△CFD，
∴S四边形ACDE=S△DOE，
在 Rt△ODE 中，OD=OA=AE=2，
∴OE=4，
∴DE=OE2−OD2=42−22=23，
∴S四边形ACDE=S△DOE=12×OD×OE=12×2×23=23.
26. （1） 300；250；150
（2） 判断：y 是 x 的一次函数，
设 y=kx+b，
∵x=10，y=300；x=11，y=250，
∴10k+b=300,11k+b=250.
解得 k=−50,b=800.
∴y=−50x+800．
经检验：x=13，y=150 也适合上述关系式，
∴y=−50x+800．
（3） 由题意可知：
W=x−8y=x−8−50x+800=−50x2+1200x−6400,
∵a=−50<0，
∴ 当 x=12 时，W 取得最大值为 800．
即当销售单价为 12 元时，每天可获得的利润最大，最大利润是 800 元．
27. （1） 3
【解析】把 4,0 代入 y=−34x+b，得：−3+b=0，解得：b=3．
（2） 如图1，过点 D 作 DE⊥x 轴于点 E，
∵ 正方形 ABCD 中，∠BAD=90∘，
∴ ∠1+∠2=90∘，
又 ∵ 直角 △OAB 中，∠2+∠3=90∘，
∴ ∠1=∠3，
在 △OAB 和 △EDA 中，
∠AOB=∠DEA,∠1=∠3,AB=AD,
∴ △OAB≌△EDAAAS，
∴ AE=OB=3，DE=OA=4，
∴ OE=4+3=7，
∴ 点 D 的坐标为 7,4．
（3） 存在．
（1）如图2，当 OM=MB=BN=NO 时，
四边形 OMBN 为菱形，
则 MN 在 OB 的中垂线上，
则 M 的纵坐标是 32，
把 y=32 代入 y=−34x+3 中，
得 x=2，即 M 的坐标是 2,32，
则点 N 的坐标为 −2,32．
（2）如图3，当 OB=BN=NM=MO=3 时，四边形 BOMN 为菱形，
∵ ON⊥BM，
∴ ON 的解析式是 y=43x，
根据题意菱形对角线的交点坐标符合以下方程组：y=−34x+3,y=43x,
解得：x=3625,y=4825,
∵ 点 O 和点 N 关于菱形对角线交点对称，
则点 N 的坐标为 7225,9625，
综上所述，点 N 的坐标为 −2,32 或者 7225,9625．
28. （1） 抛物线的对称轴为直线 x=−4am2a=−2m，
当 x=−2m 时，y=−12x=m，
则 C−2m,m，
∵∠DOB=45∘，
∴△OBD 为等腰直角三角形，
∴BD=OB=2m，则 D−2m,2m，
∴CD=m，
作 AH⊥x 轴于 H，如图 1，
∵BC∥AH，
∴BHBO=ACCO=12，
∴BH=12OB=m，
∴OH=3m，
当 x=−3m 时，y=−12x=32m，则 A−3m,32m，
当抛物线开口向下，
∵△ACD 的面积为 2，
∴12⋅m⋅m=2，解得 m=2，
当 m=2 时，D−4,4，
把 m=2，D−4,4 代入 y=ax2+4amx 得 16a−32a=4，
解得 a=−14，
∴ 抛物线解析式为 y=−14x2−2x．
（2） 当 m=2 时．对称轴为直线 x=−4，C−4,2，B−4,0，OD=42，
当点 P 在 C 点上方时，如图 2，作 PH⊥OD 于 H，
设 P−4,t，
∵∠DOB=∠BDO=45∘，
∴∠PDH=∠BDO=45∘，
∴△PDH 为等腰直角三角形，
∴PH=HD=22t−4，
∵∠POC=45∘，
∴∠POD=∠COB，
∴Rt△POH∽Rt△COB，
∴PHBC=OHOB，即 22t−42=22t−4+424，
解得 t=12，
∴P−4,12；
当点 P 在 C 点下方时，如图 3，作 CQ⊥OD 于 Q，
设 P−4,t，
易得 △CDQ 为等腰直角三角形，
∴CQ=DQ=22CD=2，
∴OQ=42−2=32，
∵∠POC=45∘，
∴∠POB=∠COQ，
∴Rt△POB∽Rt△COQ，
∴PBCQ=OBOQ，即 −t2=432，解得 t=−43，
∴P−4,−43，
综上所述，P 点坐标为 −4,12 或 −4,−43．