2021年上海市宝山区中考二模数学试卷

这是一份2021年上海市宝山区中考二模数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共6小题；共30分）
1. 下列运算正确的是
A. a2+a2=a4B. a3−a2=aC. a3⋅a2=a6D. a6÷a3=a3

2. 我国脱贫攻坚战取得了全面胜利．12.8 万个贫困村全部出列，区域性整体贫困得到解决，完成了消灭绝对贫困的艰巨任务，把“12.8 万”用科学记数法表示应是
A. 12.8×104B. 1.28×105C. 12.8×105D. 1.28×106

3. 如果直线 y=2x+m 的图象一定经过第二象限，那么 m 的取值范围是
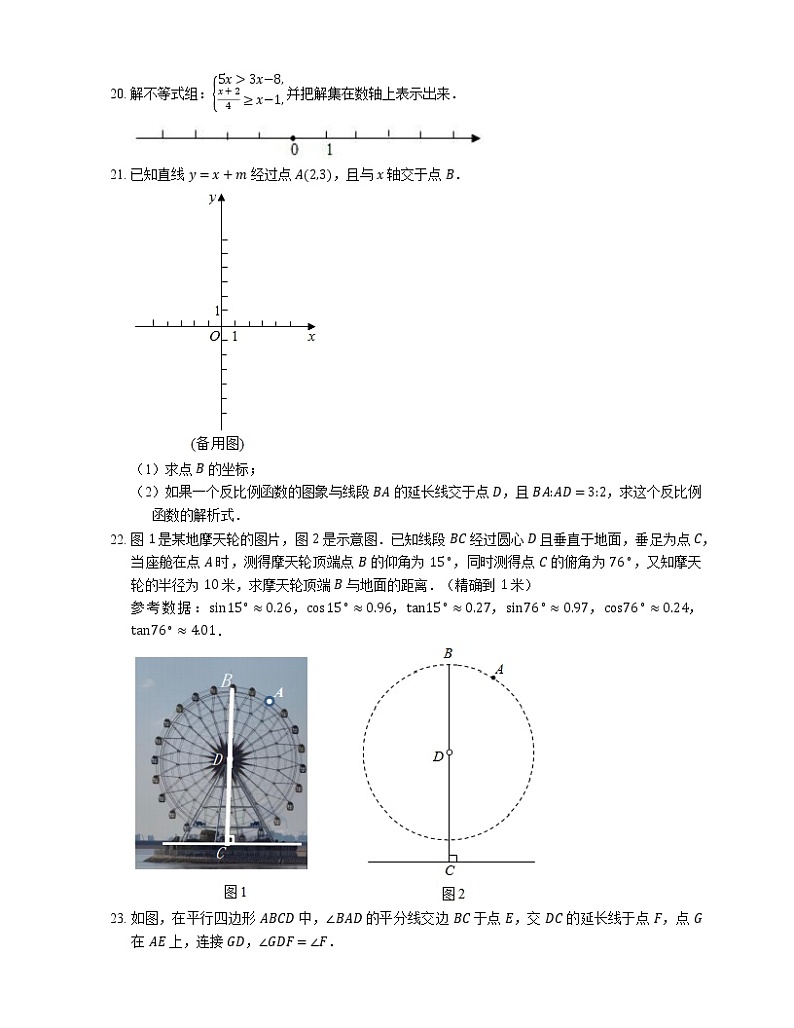
A. m>0B. m≥0C. m0 的图象上，那么 y1−y2 0（结果用 >，3x−8,x+24≥x−1, 并把解集在数轴上表示出来．

21. 已知直线 y=x+m 经过点 A2,3，且与 x 轴交于点 B．
（1）求点 B 的坐标；
（2）如果一个反比例函数的图象与线段 BA 的延长线交于点 D，且 BA:AD=3:2，求这个反比例函数的解析式．

22. 图 1 是某地摩天轮的图片，图 2 是示意图．已知线段 BC 经过圆心 D 且垂直于地面，垂足为点 C，当座舱在点 A 时，测得摩天轮顶端点 B 的仰角为 15∘，同时测得点 C 的俯角为 76∘，又知摩天轮的半径为 10 米，求摩天轮顶端 B 与地面的距离．（精确到 1 米）
参考数据：sin15∘≈0.26，cs15∘≈0.96，tan15∘≈0.27，sin76∘≈0.97，cs76∘≈0.24，tan76∘≈4.01．

23. 如图，在平行四边形 ABCD 中，∠BAD 的平分线交边 BC 于点 E，交 DC 的延长线于点 F，点 G 在 AE 上，连接 GD，∠GDF=∠F．
（1）求证：AD2=DG⋅AF；
（2）连接 BG，如果 BG⊥AE，且 AB=6，AD=9，求 AF 的长．

24. 在平面直角坐标系 xOy 中，抛物线 y=ax2+bx−1a≠0 经过点 A−2,0，B1,0 和点 D−3,n，与 y 轴交于点C．
（1）求该抛物线的表达式及点 D 的坐标；
（2）将抛物线平移，使点 C 落在点 B 处，点 D 落在点 E 处，求 △ODE 的面积；
（3）如果点 P 在 y 轴上，△PCD 与 △ABC 相似，求点 P 的坐标．

25. 如图，已知 AB⊥BC，DC⊥BC，垂足分别为点 B 、点 C，AC 与 BD 交于点 P．
（1）如果 AB=3，CD=5，以点 P 为圆心作圆，圆 P 与直线 BC 相切．
①求圆 P 的半径长；
②又 BC=8，以 BC 为直径作圆 O，试判断圆 O 与圆 P 的位置关系，并说明理由．
（2）如果分别以 AB，CD 为直径的两圆外切，求证：△ABC 与 △BCD 相似．
答案
第一部分
1. D【解析】A．a2+a2=2a2，故A不符合题意；
B．a3−a2=a2a−1，故B不符合题意；
C．a3⋅a2=a5，故C不符合题意；
D．a6÷a3=a3．故D符合题意．
2. B【解析】12.8 万 =1.28×105．
3. A【解析】根据题意得：m>0．
4. C【解析】∵ 正多边形的一个内角是 144∘，
∴ 该正多边形的一个外角为 36∘，
∵ 多边形的外角之和为 360∘，
∴ 边数 =360∘36∘=10，
∴ 这个正多边形的边数是 10．
5. B
【解析】由于总共有 11 个人，且他们的分数互不相同，第 6 的成绩是中位数，要判断是否进入前 6 名，故应知道中位数的多少．
6. C【解析】在平行四边形 ABCD 中，AD∥BC，AD=BC，AB=CD，
∵AD∥BC，∠A=∠AEC，
∴AB=CE，
∴CE=CD，故A正确；
∵ 点 E 是边 AD 的中点，
∴AD=BC=2AE=2DE，
∵AD∥BC，
∴△BFC∽△DFE，
∴BFDF=BCDE=2，
∴BF=2DF，故B正确；
∵AB=CE，FCEF=BCDE=2，
∴FC=2EF，
∴CE=3EF，
∴AB=CE=3EF，故C不正确；
∵BCDE=2，
∴S△BFC=4S△DEF，
∴S△DFC=2S△DEF，
∴S△BCD=S△BFC+S△DFC=6S△DEF，
∴S四边形ABFE=5S△DEF，故D正确．
第二部分
7. m+nm−n
8. x=4
【解析】两边平方得：3x+4=x2，
解方程得：x1=−1，x2=4，
检验：当 x=−1 时，原方程右边 =−1，所以 x=−1 不是原方程的解，
当 x=4 时，原方程左边 = 右边，所以 x=4 是原方程的解．
9. m≥−2
【解析】∵一元二次方程 12x2−2x−m=0 有两个实数根，
∴Δ=−22−4×12×−m=4+2m≥0，
解得：m≥−2，
故 m 的取值范围是 m≥−2．
10. 49
【解析】∵ 布袋里共有 9 个除颜色外其它都相同的小球，其中红球有 4 个，
∴ 从布袋中任意摸出一个球恰好为红球的概率是 49．
11. 2880
【解析】估计该区会游泳的六年级学生数约为 7200×240600=2880（人）．
12. >
【解析】∵ 点 A−3,y1 和点 B−23,y2 都在二次函数 y=ax2−2ax+ma>0 的图象上，
∴y1=9a+6a+m=15a+m，y2=49a+43a+m=169a+m，
∴y1−y2=15a+m−169a−m=1199a，
∵a>0，
∴1199a>0，
∴y1−y2>0．
13. 12.5
【解析】设良田买了 x 亩，薄田买了 y 亩，
依题意得：x+y=100,300x+5007y=10000,
解得：x=12.5,y=87.5.
即良田买了 12.5 亩．
14. 38∘
【解析】∵AC∥BD，∠C=72∘，
∴∠DBC=180∘−72∘=108∘，
∵∠ABC=70∘，
∴∠ABD=108∘−70∘=38∘．
15. 13a−b
【解析】∵AD∥BC，BC=3AD，
∴AD=13a，
∴AB=AD+DB=13a−b．
16. 32
【解析】∵AD=DC=CB，
∴∠AOD=60∘，OD⊥AC，AE=CE=12AC=32，
∴∠A=30∘，
∴OE=AE⋅tan30∘=32×33=32，
∴OA=OD=2OE=3，
∴DE=OD−OE=3−32=32．
17. 5,2 或 −5,−2
【解析】设反比例函数 y=10x 在第一象限内的图象上一对“关联点对”为 Aa,b，Bb,a 且 a>b，
∴ab=10，
∵ 这两个点之间的距离为 32，
∴AB=a−b2+b−a2=32，
∴a−b=3，
由 a−b=3,ab=10, 解得 a=5,b=2 或 a=−2,b=−5.
∴A5,2，B2,5 或 A−5,−2，B−2,−5，
∴ 距离 x 轴较近的点的坐标为 5,2 或 −5,−2．
18. 2
【解析】根据题意画出图形，过点 F 作 FG⊥BC 于点 G，
由旋转可知：EA=EF，∠AEF=90∘，
∴∠AEB+∠FEG=90∘，
∵ 四边形 ABCD 是矩形，
∴∠ABE=90∘，AB=CD=2，BC=AD=5，
∴∠BAE+∠AEB=90∘，
∴∠BAE=∠FEG，
在 △ABE 和 △EGF 中，
∠BAE=∠GEF,∠ABE=∠EGF=90∘,AE=FE,
∴△ABE≌△EGFAAS，
∴BE=FG，AB=EG=2，
设 CG=x，则 BE=BC−CG−EG=5−x−2=3−x，
∴FG=BE=3−x，
∵FG∥DC，
∴△BFG∽△BDC，
∴BGBC=FGDC，
∴5−x5=3−x2，解得 x=53，
∴CG=53，
∴BG=BC−CG=5−53=103，
FG=3−x=3−53=43，
∵FG∥DC，
∴BFDF=BGCG=10353=2．
第三部分
19. 原式=22+2+3−32+2−3=−1.
20.
5x>3x−8, ⋯⋯①x+24≥x−1, ⋯⋯②
解不等式①得：
x>−4,
解不等式②得：
x≤2,
故不等式组的解集为 −4