2020年上海市普陀区中考二模数学试卷（期中）

这是一份2020年上海市普陀区中考二模数学试卷（期中），共14页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

一、选择题（共6小题；共30分）
1. 下列计算中，正确的是
A. −22=4B. 1612=8C. 3−1=−3D. 12−2=4

2. 下列二次根式中，与 2aa>0 属同类二次根式的是
A. 2a2B. 4aC. 8a3D. 4a2

3. 关于函数 y=−2x，下列说法中错误的是
A. 函数的图象在第二、四象限B. y 的值随 x 的值增大而增大
C. 函数的图象与坐标轴没有交点D. 函数的图象关于原点对称

4. 如图，矩形 ABCD 中，对角线 AC，BD 交于点 O，如果 OB=4，∠AOB=60∘，那么矩形 ABCD 的面积等于
A. 8B. 16C. 83D. 163

5. 一个事件的概率不可能是
A. 1.5B. 1C. 0.5D. 0

6. 如图，已知 A，B，C，D 四点都在 ⊙O 上，OB⊥AC，BC=CD，在下列四个说法中，① AC=2CD；② AC=2CD；③ OC⊥BD；④ ∠AOD=3∠BOC，正确的个数是
A. 1 个B. 2 个C. 3 个D. 4 个

二、填空题（共12小题；共60分）
7. 计算：a⋅3a2= ．

8. 函数 y=1x+1 的定义域是 ．

9. 方程 5x=−x 的解是 ．

10. 已知一组数据 1，3，2，5，x，它的平均数是 3，则 x= ．

11. 如果把二次方程 x2−xy−2y2=0 化成两个一次方程，那么所得的两个一次方程分别是 ．

12. 已知一件商品的进价为 a 元，超市标价 b 元出售，后因季节原因超市将此商品打八折促销，如果促销后这件商品还有盈利，那么此时每件商品盈利 元．（用含有 a，b 的代数式表示）

13. 如果关于 x 的方程 x−22=m−1 没有实数根，那么 m 的取值范围是 ．

14. 已知正方形的半径是 4，那么这个正方形的边心距是 ．

15. 今年 3 月，上海市开展了在线学习，同时号召同学们在家要坚持体育锻炼，已知某班学生一周内在家锻炼时间的频数分布直方图如图所示．如果锻炼时间在 0∼2 小时的学生的频率是 20%，那么锻炼时间在 4∼6 小时的学生的频率是 ．

16. 如图，已知 △ABC 中，点 D，E 分别在边 AB，AC 上，DE∥BC，DC，BE 交于点 O，AB=3AD，设 BD=a，DE=b，那么向量 DO 用向量 a，b 表示是 ．

17. 将正比例函数 y=kx（k 是常数，k≠0）的图象，沿着 y 轴的一个方向平移 ∣k∣ 个单位后与 x 轴、 y 轴围成一个三角形，我们称这个三角形为正比例函数 y=kx 的坐标轴三角形，如果一个正比例函数的图象经过第一、三象限，且它的坐标轴三角形的面积为 5，那么这个正比例函数的解析式是 ．

18. 如图，在 Rt△ABC 中，∠ACB=90∘，AC=6，ctB=43，点 P 为边 AB 上一点，将 △BPC 沿着 PC 翻折得到 △BʹPC，BʹC 与边 AB 的交于点 D，如果 △BʹPD 恰好为直角三角形，那么 BP= ．

三、解答题（共7小题；共91分）
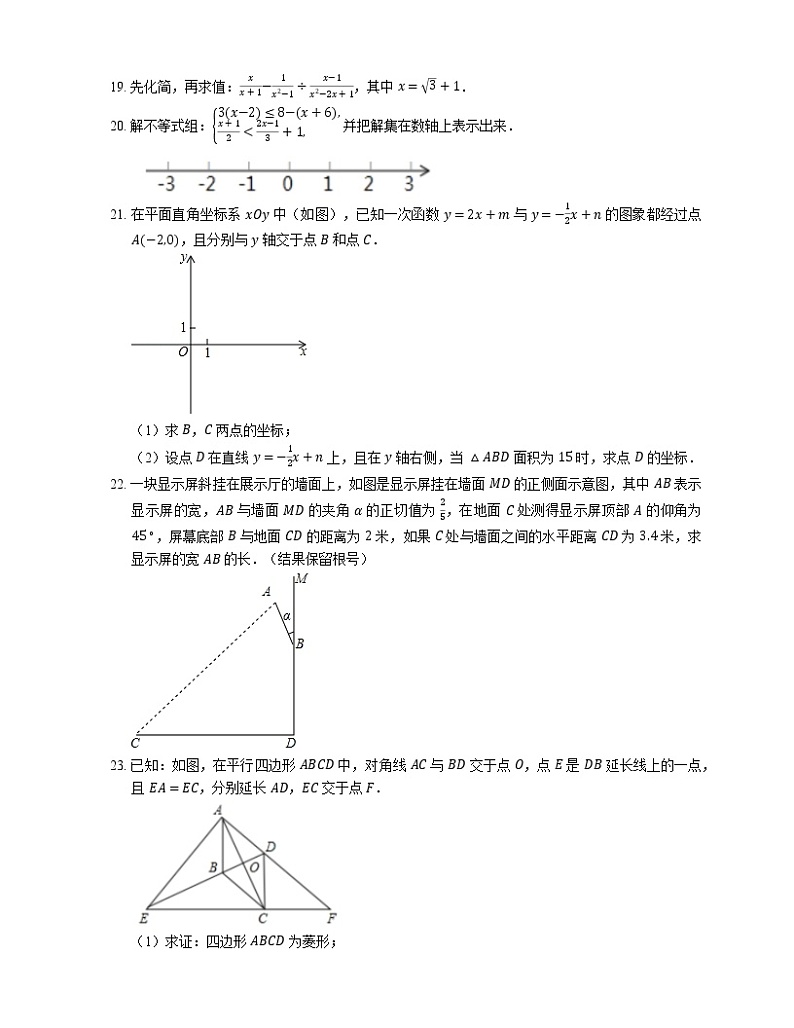
19. 先化简，再求值：xx+1−1x2−1÷x−1x2−2x+1，其中 x=3+1．

20. 解不等式组：3x−2≤8−x+6,x+12<2x−13+1, 并把解集在数轴上表示出来．

21. 在平面直角坐标系 xOy 中（如图），已知一次函数 y=2x+m 与 y=−12x+n 的图象都经过点 A−2,0，且分别与 y 轴交于点 B 和点 C．
（1）求 B，C 两点的坐标；
（2）设点 D 在直线 y=−12x+n 上，且在 y 轴右侧，当 △ABD 面积为 15 时，求点 D 的坐标．

22. 一块显示屏斜挂在展示厅的墙面上，如图是显示屏挂在墙面 MD 的正侧面示意图，其中 AB 表示显示屏的宽，AB 与墙面 MD 的夹角 α 的正切值为 25，在地面 C 处测得显示屏顶部 A 的仰角为 45∘，屏幕底部 B 与地面 CD 的距离为 2 米，如果 C 处与墙面之间的水平距离 CD 为 3.4 米，求显示屏的宽 AB 的长．（结果保留根号）

23. 已知：如图，在平行四边形 ABCD 中，对角线 AC 与 BD 交于点 O，点 E 是 DB 延长线上的一点，且 EA=EC，分别延长 AD，EC 交于点 F．
（1）求证：四边形 ABCD 为菱形；
（2）如果 ∠AEC=2∠BAC，求证：EC⋅CF=AF⋅AD．

24. 在平面直角坐标系 xOy 中（如图），已知点 A 在 x 轴的正半轴上，且与原点的距离为 3，抛物线 y=ax2−4ax+3a≠0 经过点 A，其顶点为 C，直线 y=1 与 y 轴交于点 B，与抛物线交于点 D（在其对称轴右侧），连接 BC，CD．
（1）求抛物线的表达式及点 C 的坐标；
（2）点 P 是 y 轴的负半轴上的一点，如果 △PBC 与 △BCD 相似，且相似比不为 1，求点 P 的坐标；
（3）将 ∠CBD 绕着点 B 逆时针方向旋转，使射线 BC 经过点 A，另一边与抛物线交于点 E（点 E 在对称轴的右侧），求点 E 的坐标．

25. 如图，已知在四边形 ABCD 中，AD∥BC，∠ABC=90∘，以 AB 为直径的 ⊙O 交边 DC 于 E，F 两点，AD=1，BC=5，设 ⊙O 的半径长为 r．
（1）连接 OF，当 OF∥BC 时，求 ⊙O 的半径长；
（2）过点 O 作 OH⊥EF，垂足为点 H，设 OH=y，试用 r 的代数式表示 y；
（3）设点 G 为 DC 的中点，连接 OG，OD，△ODG 是否能成为等腰三角形?如果能，试求出 r 的值；如不能，试说明理由．
答案
第一部分
1. D【解析】A、 −22=−4，本选项计算错误；
B、 1612=16=4，本选项计算错误；
C、 3−1=13，本选项计算错误；
D、 12−2=1122=4，本选项计算正确；
故选：D．
2. C【解析】A．2a2=2a，与 2a 的被开方数不同，则它们不是同类二次根式，故本选项不合题意；
B．4a=2a，与 2a 的被开方数不同，则它们不是同类二次根式，故本选项不合题意；
C．8a3=2a2a，与 2a 的被开方数相同，则它们是同类二次根式，故本选项正确；
D．4a2=2a 与 2a 的被开方数不同，则它们不是同类二次根式，故本选项不合题意，
故选：C．
3. B【解析】∵ 反比例函数 y=−2x 的系数 k=−2<0，
∴ 该函数的图象在第二、四象限，则选项A正确；
在每个象限内，y 随 x 的增大而增大，则选项B错误；
函数的图象与坐标轴没有交点，则选项C正确；
函数的图象关于原点对称，则选项D正确．
故选：B．
4. D【解析】∵ 四边形 ABCD 是矩形，
∴∠BAD=90∘，AO=CO=12AC，BO=DO=12BD，AC=BD=2OB=8，
∴OA=OB=4，
∵∠AOB=60∘，
∴△AOB 是等边三角形，
∴AB=OB=4，
∴AD=BD2−AB2=82−42=43，
∴ 矩形 ABCD 的面积 =AB×AD=4×43=163．
5. A
【解析】一个事件的概率最大是 1，最小是 0，故选项A错误．
6. C【解析】∵OB⊥AC，BC=CD，
∴AB=BC，CD=BC，
∴AC=2CD，故①正确；
AC OC⊥BD，故③正确；
∠AOD=3∠BOC，故④正确；
故选：C．
第二部分
7. 9a3
【解析】原式=a⋅9a2=9a3．
8. x≠−1
【解析】由题意得：x+1≠0，解得：x≠1．
9. x=0
【解析】把方程 5x=−x 两边平方，得 5x=x2，
∴x2−5x=0，
∴xx−5=0，
∴x=0 或 x−5=0，
∴x1=0，x2=5．
检验：把 x1=0，x2=5 代入方程 5x=−x，
可知 x1=0 是原方程的根，x2=5 是不符合原方程，
∴ 原方程的解为 x=0．
10. 4
【解析】由题意得：1+3+2+5+x5=3，解得：x=4．
11. x−2y=0 或 x+y=0
【解析】∵x2−xy−2y2=0，
∴x−2yx+y=0，
∴x−2y=0 或 x+y=0．
12. 0.8b−a
【解析】根据题意得，每件商品盈利 0.8b−a 元．
13. m<1
【解析】∵ 关于 x 的方程 x−22=m−1 没有实数根，
∴m−1<0，解得 m<1，
所以 m 的取值范围是 m<1．
14. 22
【解析】如图，根据正方形的性质知：△BOC 是等腰直角三角形，
过 O 作 OE⊥BC 于 E．
∵ 正方形的半径是 4，
∴BO=4，
∴OE=BE=22BO=22．
15. 0.25
【解析】∵ 锻炼时间在 0∼2 小时的学生的频率是 20%，人数为 8，
∴ 被调查的总人数为 8÷20%=40（人），
则锻炼时间在 4∼6 小时的学生的频率是 10÷40=0.25．
16. −14a+34b
【解析】∵DE∥BC，ADAB=DEBC=13，
∴BC=3DE，
∵DE=b，
∴BC=3b，
∵△DOE∽△COB，
∴ODOC=DEBC=13，
∴OD=13OC=14CD，
∵DC=DB+BC，
∴DC=−a+3b，
∴DO=−14a+34b．
17. y=10x
【解析】∵ 正比例函数的图象经过第一、三象限，
∴k>0，
∴ 当正比例函数 y=kx（k 是常数，k≠0）的图象，沿着 y 轴向上平移 ∣k∣ 个单位时，所得函数的解析式为 y=kx+k，
如图示：
∴ 与 x 轴的交点坐标为 −1,0，与 y 轴的交点坐标为 0,k，
∴ 它的坐标轴三角形的面积为 5，
∴1×k2=5，
∴k=10，
∴ 这个正比例函数的解析式是 y=10x，
∵ 当正比例函数 y=kx（k 是常数，k≠0）的图象，沿着 y 轴向下平移 ∣k∣ 个单位时，所得函数的解析式为 y=kx−k，
如图示：
∴ 与 x 轴的交点坐标为 1,0，与 y 轴的交点坐标为 0,−k，
∵ 它的坐标轴三角形的面积为 5，
∴1×k2=5，
∴k=10，
∴ 这个正比例函数的解析式是 y=10x．
18. 4 或 85
【解析】如图 1 中，当 ∠DPBʹ=90∘ 时，过点 C 作 CH⊥AB 于 H．
∵ctB=BCAC=43，AC=6，
∴BC=8，
∴AB=AC2+BC2=82+62=10，
∵12⋅BC⋅AC=12⋅AB⋅CH，
∴CH=245，
∵∠B+∠A=90∘，∠Bʹ+∠PDBʹ=90∘，∠B=∠Bʹ，∠PDBʹ=∠ADC，
∴∠ADC=∠A，
∴AC=CD=6，
∵CH⊥AD，
∴AH=DH=AC2−CH2=62−2452=185，
∴BD=AB−AD=10−365=145，DBʹ=CBʹ−CD=CB−CA=2，设 PB=x，
在 Rt△PDBʹ 中，则有 x2+145−x2=22，解得 x=85 或 65（舍弃）；
如图 2 中，当 ∠PDBʹ=90∘ 时，设 BP=PBʹ=x．
在 Rt△PDBʹ 中，则有 x2=325−x2+1652，解得 x=4．
综上所述，满足条件的 PB 的值为 85 或 4．
第三部分
19. 原式=xx+1−1x+1x−1⋅x−12x−1=xx+1−1x+1=x−1x+1.
当 x=3+1 时，
原式=3+1−13+1+1=33+2=23−3.
20.
3x−2≤8−x+6, ⋯⋯①x+12<2x−13+1. ⋯⋯②
解不等式 ①，得：
x≤2.
解不等式 ②，得：
x>−1.
将不等式解集表示在数轴上如下：
所以不等式组的解集为
−121. （1） 将 A−2,0 代入 y=2x+m，解得 m=4，
∴y=2x+4，
令 x=0，则 y=4，即 B0,4；
将 A−2,0 代入 y=−12x+n，解得 n=−1，
∴y=−12x−1，令 x=0，则 y=−1，即 C0,−1．
（2） 如图，过 D 作 DE⊥BC 于 E．
当 △ABD 的面积为 15 时，S△ABC+S△BCD=15，
即 12AO×BC+12DE×BC=15，
∴12×2×5+12×DE×5=15，
∴DE=4，
y=−12x−1 中，令 x=4，则 y=−3，
∴D4,−3．
22. 过 A 作 AP⊥DM 于 P，AH⊥CD 于 H，过 B 作 BN⊥AH 于 N，
∵tan∠ABM=25，
∴ 设 AP=BN=2x，AN=PB=5x，
∵BD=2，CD=3.4，
∴HN=2，CH=3.4−2x，
∴AH=5x+2，
∵∠ACD=45∘，
∴AH=CH，
∴3.4−2x=5x+2，解得：x=0.2，
∴PB=1，AP=0.4，
∴AB=PB2−AP2=0.42+12=295（米）．
答：显示屏的宽 AB 的长为 295 米．
23. （1） ∵ 四边形 ABCD 是平行四边形，
∴OA=OC，
又 ∵EA=EC，
∴EO⊥AC，
∴ 四边形 ABCD 是菱形．
（2） ∵∠AEB=∠CEB=12∠AEC，平行四边形 ABCD 为菱形，
∴∠AEB=∠CEB=∠BAC=∠BCA=∠DAC=∠DCA，∠CDF=∠DAC+∠DCA=∠AEF，
∴△FCD∽△FAE，
∴FCFA=CDAE，
∵CD=AD，AE=CE，
∴FCFA=ADCE，即 EC⋅CF=AF⋅AD．
24. （1） ∵ 点 A 在 x 轴的正半轴上，且与原点的距离为 3，
∴A3,0，
把 A3,0 代入抛物线 y=ax2−4ax+3 中得：0=9a−12a+3，
∴a=1，
∴ 抛物线表达式为：y=x2−4x+3，y=x2−4x+3=x−22−1，
∴C2,−1．
（2） 当 y=1 时，x2−4x+3=1，解得：x1=2−2，x2=2+2，
由题意得：D2+2,1，
∵B0,1，C2,−1，
∴BC=22+1+12=22，BD=2+2，
∵∠DBC=∠PBC=45∘，且相似比不为 1，只能 △CBP∽△DBC，
∴CBDB=BPBC，即 222+2=BP22，
∴BP=8−42，
∴P0,42−7．
（3） 连接 AC，过 E 作 EH⊥BD 于 H．
由旋转得：∠CBD=∠ABE，
∴∠EBD=∠ABC，
∵AB2=32+12=10，BC2=22+22=4，AC2=12+12=2，
∴AB2=BC2+AC2，
∴△ABC 是等腰直角三角形，且 ∠ACB=90∘，
∴tan∠ABC=ACBC=222=12，
∴tan∠EBD=12=EHBH，
设 EH=m，则 BH=2m，
∴E2m,m+1，
∵ 点 E 在抛物线上，
∴2m2−4×2m+3=m+1，4m2−9m+2=0，
解得：m1=2，m2=14（舍），
∴E4,3．
25. （1） ∵OF∥BC，OA=OB，
∴OF 为梯形 ABCD 的中位线，
∴OF=12AD+BC=121+5=3，即 ⊙O 的半径长为 3．
（2） 连接 OD，OC，过点 D 作 DM⊥BC 于 M，如图 1 所示：
∵AD∥BC，∠ABC=90∘，且 DM⊥BC，
∴ 四边形 ABMD 为矩形，则 BM=AD=1，
∴CM=BC−BM=4，
∴DC=DM2+CM2=2r2+42=2r2+4，
∵ 四边形 ABCD 的面积 =△DOC 的面积 +△AOD 的面积 +△BOC 的面积，
∴121+5×2r=12×2r2+4×y+12r×1+12r×5，
整理得：y=3rr2+4r2+4．
（3） △ODG 能成为等腰三角形，理由如下：
∵ 点 G 为 DC 的中点，OA=OB，
∴OG 是梯形 ABCD 的中位线，
∴OG∥AD，OG=12AD+BC=121+5=3，
DG=12CD=r2+4，
由勾股定理得：OD=OA2+AD2=r2+12=r2+1．
分三种情况：
① DG=DO 时，则 r2+4=r2+1，无解；
② OD=OG 时，如图 2 所示：
r2+1=3，解得：r=22；
③ GD=GO 时，作 OH⊥CD 于 H，如图 3 所示：
∠GOD=∠GDO，
∵OG∥AD，
∴∠ADO=∠GOD，
∴∠ADO=∠GDO，
∴DO 是 ∠ADG 的平分线，
由题意知：OA⊥AD，又 OH⊥CD，
∴OA=OH，则此时圆 O 和 CD 相切，不合题意．
综上所述，△ODG 能成为等腰三角形，r=22．