2020年上海市松江区中考二模数学试卷（期中）

这是一份2020年上海市松江区中考二模数学试卷（期中），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共6小题；共30分）
1. 下列实数中，有理数是
A. 3B. 34C. πD. 3.14

2. 如果将抛物线 y=x2+2 向左平移 1 个单位，那么所得新抛物线的解析式为
A. y=x−12+2B. y=x+12+2
C. y=x2+1D. y=x2+3

3. 不等式组 x+2>0,6−2x<2 的解集是
A. x>−2B. x<−2C. x>2D. x<2

4. 某校田径运动会有 13 名同学参加女子百米赛跑，她们预赛的成绩各不相同，取前 6 名参加决赛，小玥已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这 13 名同学成绩的
A. 方差B. 极差C. 平均数D. 中位数

5. 如果一个多边形的每一个内角都是 135∘，那么这个多边形的边数是
A. 5B. 6C. 8D. 10

6. 如图，已知 △ABC 中，AC=2，AB=3，BC=4，点 G 是 △ABC 的重心．将 △ABC 平移，使得顶点 A 与点 G 重合．那么平移后的三角形与原三角形重叠部分的周长为
A. 2B. 3C. 4D. 4.5

二、填空题（共12小题；共60分）
7. 化简：a3= ．

8. 方程组 x+y=2,xy=−3 的解是 ．

9. 函数 y=1x+2 的定义域是 ．

10. 若关于 x 的一元二次方程 x2+x−m=0 有两个实数根，则 m 的取值范围是 ．

11. 一枚材质均匀的骰子，六个面的点数分别是 1，2，3，4，5，6，掷一次骰子，掷的点数大于 2 的概率是 ．

12. 已知点 P−2,y1 和点 Q−1,y2 都在二次函数 y=−x2+c 的图象上，那么 y1 与 y2 的大小关系是 ．

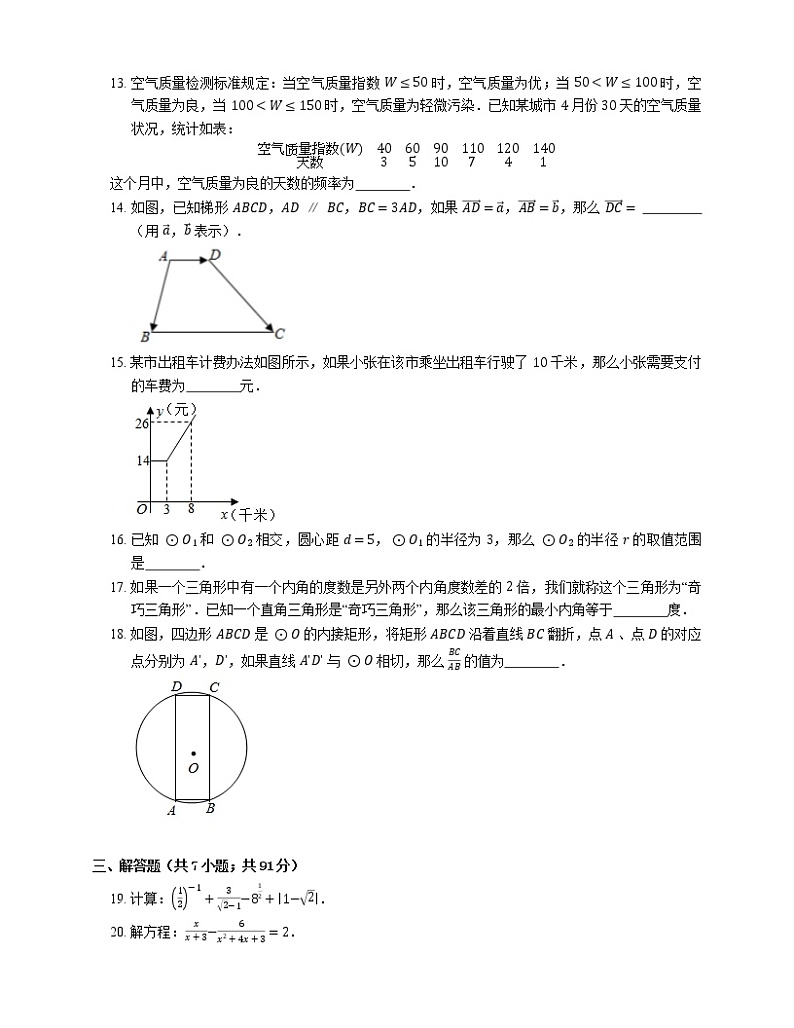
13. 空气质量检测标准规定：当空气质量指数 W≤50 时，空气质量为优；当 50空气质量指数W406090110120140天数3510741
这个月中，空气质量为良的天数的频率为 ．

14. 如图，已知梯形 ABCD，AD∥BC，BC=3AD，如果 AD=a，AB=b，那么 DC= （用 a，b 表示）．

15. 某市出租车计费办法如图所示，如果小张在该市乘坐出租车行驶了 10 千米，那么小张需要支付的车费为 元．

16. 已知 ⊙O1 和 ⊙O2 相交，圆心距 d=5，⊙O1 的半径为 3，那么 ⊙O2 的半径 r 的取值范围是 ．

17. 如果一个三角形中有一个内角的度数是另外两个内角度数差的 2 倍，我们就称这个三角形为“奇巧三角形”．已知一个直角三角形是“奇巧三角形”，那么该三角形的最小内角等于 度．

18. 如图，四边形 ABCD 是 ⊙O 的内接矩形，将矩形 ABCD 沿着直线 BC 翻折，点 A 、点 D 的对应点分别为 Aʹ，Dʹ，如果直线 AʹDʹ 与 ⊙O 相切，那么 BCAB 的值为 ．

三、解答题（共7小题；共91分）
19. 计算：12−1+32−1−812+1−2．

20. 解方程：xx+3−6x2+4x+3=2．

21. 如图，在平面直角坐标系内 xOy 中，某一次函数的图象与反比例函数的 y=3x 的图象交于 A1,m，Bn,−1 两点，与 y 轴交于 C 点．
（1）求该一次函数的解析式；
（2）求 ACBC 的值．

22. 如图是某地下停车库入口的设计示意图，已知坡道 AB 的坡比 i=1:2.4，AC 的长为 7.2 米，CD 的长为 0.4 米．按规定，车库坡道口上方需张贴限高标志，根据图中所给数据，确定该车库入口的限高数值（即点 D 到 AB 的距离）．

23. 如图，已知 AB，AC 是 ⊙O 的两条弦，且 AO 平分 ∠BAC．点 M，N 分别在弦 AB，AC 上，满足 AM=CN．
（1）求证：AB=AC；
（2）连接 OM，ON，MN，求证：MNAB=OMOA．

24. 如图，在平面直角坐标系 xOy 中，抛物线 y=−x2+bx+3 与 x 轴和 y 轴的正半轴分别交于 A，B 两点，且 OA=OB，抛物线的顶点为 M，连接 AB，AM．
（1）求这条抛物线的表达式和点 M 的坐标；
（2）求 sin∠BAM 的值；
（3）如果 Q 是线段 OB 上一点，满足 ∠MAQ=45∘，求点 Q 的坐标．

25. 如图，已知梯形 ABCD 中，AD∥BC，AB⊥BC，AD（1）如果 CE=CD，求证：AD=AE；
（2）连接 DE，如果存在点 E，使得 △ADE，△BCE 和 △CDE 两两相似，求 AD 的长；
（3）设点 E 关于直线 CD 的对称点为 M，点 D 关于直线 CE 的对称点为 N，如果 AD=23，且 M 在直线 AD 上时，求 DNEM 的值．
答案
第一部分
1. D【解析】A、 3 是无理数，不合题意；
B、 34 是无理数，不合题意；
C、 π 是无理数，不合题意；
D、 3.14 是有理数，符合题意．
故选：D．
2. B【解析】抛物线 y=x2+2 的顶点坐标为 0,2，点 0,2 向左平移 1 个单位长度所得对应点的坐标为 −1,2，所以平移后的抛物线的解析式为 y=x+12+2．
3. C【解析】解不等式 x+2>0，得：x>−2，
解不等式 6−2x<2，得：x>2，
则不等式组的解集为 x>2．
4. D【解析】13 个不同的分数按从小到大排序后，中位数及中位数之后的共有 7 个数，故只要知道自己的分数和中位数就可以知道是否能进行决赛，故选D．
5. C
【解析】多边形的边数是：n=360∘180∘−135∘=8，即该多边形是八边形．
6. B【解析】如图，
∵ 将 △ABC 平移得到 △GEF，
∴GE∥AB，GF∥AC，
∴∠GMN=∠B，∠GNM=∠C，
∴△GMN∽△ABC，
∴△GMN的周长△ABC的周长=GDAD，
∵ 点 G 是 △ABC 的重心，
∴AG=2GD，
∴△GMN的周长△ABC的周长=13，
∴△GMN 的周长 =13×2+3+4=3．
第二部分
7. aa
【解析】原式=a2⋅a=aa．
8. x=3,y=−1 或 x=−1,y=3
【解析】方程组 x+y=2, ⋯⋯①xy=−3. ⋯⋯②
由 ① 得，y=2−x. ⋯⋯③
把 ③ 代入 ② 得，x2−x=−3．
解得：x1=3，x2=−1．
把 x1=3，x2=−1 分别代入 ③ 得，y1=−1，y2=3．
∴ 原方程组的解为 x=3,y=−1 或 x=−1,y=3.
9. x≠−2
【解析】∵ 函数 y=1x+2，
∴x+2≠0，解得，x≠−2．
10. m≥−14
【解析】∵ 关于 x 的一元二次方程 x2+x−m=0 有两个实数根，
∴Δ≥0，
∴Δ=1−4−m≥0，即 m≥−14．
11. 23
【解析】∵ 在这 6 种情况中，掷的点数大于 2 的有 3，4，5，6 共 4 种结果，
∴ 掷的点数大于 2 的概率为 46=23．
12. y1【解析】∵ 二次函数 y=−x2+c 的开口向下，对称轴为 y 轴，
∴ 当 x<0 时，y 随 x 的增大而增大，
∵−2<−1，
∴y113. 0.5
【解析】这个月中，空气质量为良的天数的频率为 5+1030=0.5．
14. 2a+b
【解析】∵AD∥BC，BC=3AD，
∴BC=3AD=3a，
∵DC=DA+AB+BC，
∴DC=−a+b+3a=2a+b．
15. 30.8
【解析】由图象可知，出租车的起步价是 14 元，在 3 千米内只收起步价，
设超过 3 千米函数解析式为 y=kx+b，
则 3k+b=14,8k+b=26, 解得 k=2.4,b=6.8,
∴ 超过 3 千米时（x>3）所需费用 y 与 x 之间的函数关系式是 y=2.4x+6.8，
∴ 出租车行驶了 10 千米，则 y=2.4×10+6.8=30.8（元）．
16. 2【解析】由题意可知：3−r<5<3+r，解得：217. 22.5
【解析】设直角三角形的最小内角为 x，另一个内角为 y，
由题意得，x+y=90∘,2x−y=90∘,
解得：x=22.5∘,y=67.5∘.
答：该三角形的最小内角等于 22.5∘．
18. 24
【解析】设直线 AʹDʹ 与 ⊙O 相切于 G，连接 OC，OG 交 BC 于 E．
∵ 将矩形 ABCD 沿着直线 BC 翻折，
∴AD=BC=AʹDʹ，AB=CD=CDʹ=AʹB，
过 O 作 OH⊥CD，
∴CH=12CD，
∵ 直线 AʹDʹ 与 ⊙O 相切，
∴OG⊥AʹDʹ，
∵BC∥AʹDʹ，
∴OG⊥BC，
∴ 则四边形 OECH 是矩形，CE=BE=12BC，
∴CH=OE，
设 AB=CD=CDʹ=AʹB=x，
∴OE=12x，
∴OC=OG=32x，
∴CE=OC2−OE2=3x22−12x2=2x，
∴BC=2CE=22x，
∴ABBC=x22x=24．
第三部分
19. 原式=2+32+1−22+2−1=2+32+3−22+2−1=22+4.
20. 去分母得：
xx+1−6=2x2+8x+6.
去括号得：
x2+x−6=2x2+8x+6.
移项得：
x2+x−6−2x2−8x−6=0.
整理得：
x2+7x+12=0.
即
x+3x+4=0.
解得：
x1=−3,x2=−4.
经检验，x1=−3 是增根，舍去，
∴ 原方程的根是 x=−4．
21. （1） 设一次函数解析式为 y=kx+bk≠0．
又 ∵A1,m，Bn,−1 在反比例函数 y=3x 的图象上，
∴m=31，−1=3n，
∴m=3，n=−3．
∴A1,3，B−3,−1．
一次函数 y=kx+b 的图象过 A1,3，B−3,−1．
∴k+b=3,−3k+b=−1,
∴k=1,b=2,
∴ 所求一次函数的解析式是 y=x+2．
（2） 过点 A，B 分别作 y 轴垂线，垂足为分别 D，E，
过点 B 作 BF 垂直于 AD 的延长线于点 F，BF 交 y 轴于点 G．
∵y=x+2，令 x=0，得 y=2，
∴OC=2，则 AF∥BE，
∴BCAB=BGBF=BGBG+GF=33+1=34，
∴ACBC=13．
22. 如图，延长 CD 交 AB 于 E，
∵i=1:2.4，
∴tan∠CAB=12.4=512，
∴CEAC=512，
∵AC=7.2，
∴CE=3，
∵CD=0.4，
∴DE=2.6，
过点 D 作 DH⊥AB 于 H，
∴∠EDH=∠CAB，
∵tan∠CAB=512，
∴cs∠EDH=cs∠CAB=1213，
DH=DE×cs∠EDH=2.6×1213=2.4．
答：该车库入口的限高数值为 2.4 米．
23. （1） 过点 O 作 OD⊥AB 于点 D，OE⊥AC 于点 E，如图所示：
∵AO 平分 ∠BAC，
∴OD=OE．
∵AD2=AO2−OD2，AE2=AO2−OE2，
∴AD=AE．
∵OD⊥AB，OE⊥AC，
∴AB=2AD，AC=2AE，
∴AB=AC．
（2） 连接 OB，OM，ON，MN，如图所示．
∵AM=CN，AB=AC，
∴BM=AN．
∵OA=OB，
∴∠B=∠BAO．
∵∠BAO=∠OAN，
∴∠B=∠OAN．
∴△BOM≌△AONSAS．
∴∠BOM=∠AON，OM=ON．
∴∠AOB=∠MON．
∴△NOM∽△BOA．
∴MNAB=OMOA．
24. （1） ∵ 抛物线 y=−x2+bx+3 与 y 轴交于 B 点，
令 x=0 得 y=3，
∴B0,3，
∵AO=BO，
∴A3,0，
把 A3,0 代入 y=−x2+bx+3，
得 −9+3b+3=0，解得 b=2，
∴ 这条抛物线的表达式 y=−x2+2x+3，顶点 M1,4．
（2） ∵A3,0，B0,3，M1,4，
∴BM2=2，AB2=18，AM2=20，
∴∠MBA=90∘，
∴sin∠BAM=BMAM=225=1010．
（3） ∵OA=OB，
∴∠OAB=45∘．
∵∠MAQ=45∘，
∴∠BAM=∠OAQ．
由（2）得 sin∠BAM=1010，
∴sin∠OAQ=1010．
∴tan∠OAQ=13．
∴OQOA=OQ3=13．
∴OQ=1．
∴Q0,1．
25. （1） 如图，过 C 点作 CF⊥AD，交 AD 的延长线于 F，
∵AD∥BC，AB⊥BC，AB=BC，
∴ 四边形 ABCF 是正方形，
∴AB=BC=CF=FA，
又 ∵CE=CD，
∴Rt△CBE≌Rt△CFDHL，
∴BE=FD，
∴AD=AE．
（2） ①若 ∠EDC=90∘ 时，
若 △ADE，△BCE 和 △CDE 两两相似，
那么 ∠A=∠B=∠EDC=90∘，∠ADE=∠BCE=∠DCE=30∘，
在 △CBE 中，
∵BC=1，
∴BE=13=33，CE=233，
∵AB=1，
∴AE=1−33=3−33，
∴AD=3AE=3×3−33=33−33=3−1，
此时 EDCE=2AE2BE=AEBE=3−33×33=3−1≠BEEC，
∴△CDE 与 △ADE，△BCE 不相似；
②如图，若 ∠DEC=90∘ 时，
∵∠ADE+∠A=∠BEC+∠DEC，∠DEC=∠A=90∘，
∴∠ADE=∠BEC，且 ∠A=∠B=90∘，
∴△ADE∽△BEC，
∴∠AED=∠BCE，
若 △CDE 与 △ADE 相似，
∵AB 与 CD 不平行，
∴∠AED 与 ∠EDC 不相等，
∴∠AED=∠BCE=∠DCE，
∴ 若 △CDE 与 △ADE，△BCE 相似，
∴AEBC=DEEC=BEBC，
∴AE=BE，
∵AB=1，
∴AE=BE=12，
∴AD=14．
（3） 连接 EM 交 CD 于 Q，连接 DN 交 CE 于 P，连接 ED，CM，作 CF⊥AD 于 F，
∵E 关于直线 CD 的对称点为 M，点 D 关于直线 CE 的对称点为 N，
∴∠CPD=∠CQE=90∘，DC 垂直平分 EM，∠PCD=∠QCE，
∴△CDP∽△CEQ，
∴DPEQ=DCCE，
∵AD∥BC，AB⊥BC，AD=23，AB=BC=1，
∴CD=103，
∵CD 垂直平分 EM，
∴DE=DM，CE=CM，
在 Rt△CBE 和 Rt△CFM 中，
CB=CF，EC=CM，
∴Rt△CBE≌Rt△CFMHL，
∴BE=FM，
设 BE=x，则 FM=x，
∵ED=DM，且 AE2+AD2=DE2，
∴1−x2+49=13+x2，
∴x=12，
∴CE=52，
∴DCCE=103×25=223，
∵DN=2DP，EM=2EQ，
∴DNEM=2DP2EQ=DCCE=223．