

2020年北京市房山区中考二模数学试卷
展开一、选择题(共8小题;共40分)
1. 在迎来庆祝新中国成立 70 周年之后,对于中国而言,2020 年又将是一个新的时间坐标.过去 40 年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将 820000000 用科学记数法表示为
A. 8.2×109B. 0.82×109C. 8.2×108D. 82×107
2. 如图是某个几何体的三视图,该几何体是
A. 长方体B. 三棱柱C. 正方体D. 圆柱
3. 实数 a,b 在数轴上的对应点的位置如图所示,则正确的结论是
A. b
4. 《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于 2020 年 5 月 1 日起施行,施行的目的在于加强生活垃圾管理,改善城乡环境,保障人体健康.下列垃圾分类标志,是中心对称图形的是
A. B.
C. D.
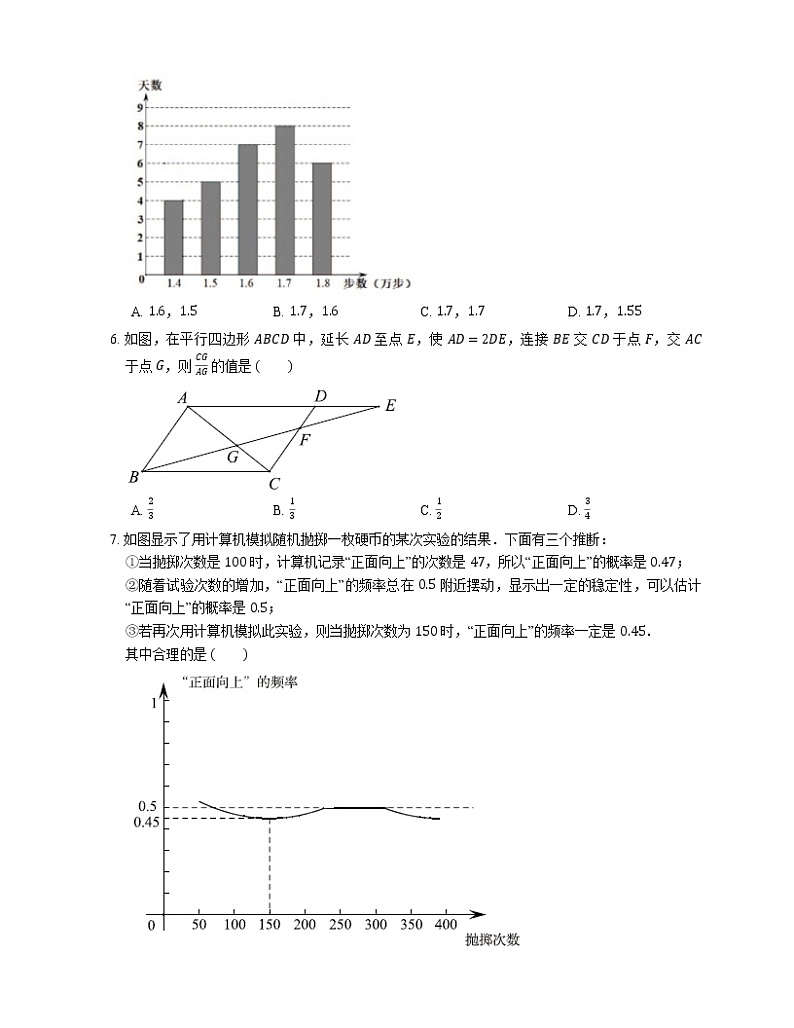
5. 李老师是一位运动达人,他通过佩戴智能手环来记录自已一个月(30 天)每天所走的步数,并绘制成如下统计图,在每天所走的步数这组数据中,众数和中位数分别是
A. 1.6,1.5B. 1.7,1.6C. 1.7,1.7D. 1.7,1.55
6. 如图,在平行四边形 ABCD 中,延长 AD 至点 E,使 AD=2DE,连接 BE 交 CD 于点 F,交 AC 于点 G,则 CGAG 的值是
A. 23B. 13C. 12D. 34
7. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果.下面有三个推断:
①当抛掷次数是 100 时,计算机记录“正面向上”的次数是 47,所以“正面向上”的概率是 0.47;
②随着试验次数的增加,“正面向上”的频率总在 0.5 附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是 0.5;
③若再次用计算机模拟此实验,则当抛掷次数为 150 时,“正面向上”的频率一定是 0.45.
其中合理的是
A. ①B. ②C. ①②D. ①③
8. 2020 年是 5G 爆发元年,三大运营商都在政策的支持下,加快着 5G 建设的步伐.某通信公司实行的 5G 畅想套餐,部分套餐资费标准如下:
小武每月大约使用国内数据流量 49 GB,国内主叫 350 分钟,若想使每月付费最少,则他应预定的套餐是
A. 套餐 1B. 套餐 2C. 套餐 3D. 套餐 4
二、填空题(共8小题;共40分)
9. 若分式 x+1x−1 值为 0,则 x 的值是 .
10. 如图,扇形 AOB,通过测量、计算,得 AB 的长约为 cm(π 取 3.14,结果保留一位小数)
11. 如图,若在象棋棋盘上建立直角坐标系,使“帅”位于点 −3,−2,“炮”位于点 −2,0,则“兵”位于的点的坐标为 .
12. 如图,一个大正方形被分成两个正方形和两个一样的矩形,请根据图形,写出一个含有 a,b 的正确的等式 .
13. 如果 m+n=4,那么代数式 m2+n2m+2n⋅2mm+n 的值为 .
14. 已知一组数据 x1,x2,x3,⋯,xn 的方差是 S2,那么另一组数据 x1−3,x2−3,x3−3,⋯,xn−3 的方差是 .
15. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
译文:“有一根竹子,原高二丈(1丈 =10 尺),现被风折断,竹梢触地面处与竹根的距离为 6 尺,问折断处离地面的高度为多少尺?”
如图,我们用点 A,B,C 分别表示竹梢,竹根和折断处,设折断处离地面的高度 BC 为 x 尺,则可列方程为 .
16. 下面是“作一个 30∘ 角”的尺规作图过程.
已知:平面内一点 A.
求作:∠A,使得 ∠A=30∘.
作法:如图.
(1)作射线 AB;
(2)在射线 AB 上取一点 O,以 O 为圆心,OA 为半径作圆,与射线 AB 相交于点 C;
(3)以 C 为圆心,OC 为半径作弧,与 ⊙O 交于点 D,作射线 AD.则 ∠DAB 即为所求的角.
请回答:该尺规作图的依据是 .
三、解答题(共12小题;共156分)
17. 计算:18−15−1+4sin30∘+2−1.
18. 解不等式组:3x+1<2x,x−12
19. 如图,在 △ABC 中,BD 平分 ∠ABC 交 AC 于点 D,DE∥AB 交 BC 于点 E,F 是 BD 中点.
求证:EF 平分 ∠BED.
20. 已知关于 x 的一元二次方程 kx2−4x+3=0.
(1)当 k=1 时,求此方程的根;
(2)若此方程有两个不相等的实数根,求 k 的取值范围.
21. 如图,菱形 ABCD 中,分别延长 DC,BC 至点 E,F,使 CE=CD,CF=CB,连接 DB,BE,EF,FD.
(1)求证:四边形 DBEF 是矩形;
(2)若 AB=5,cs∠ABD=35,求 DF 的长.
22. 在平面直角坐标系 xOy 中,反比例函数 y=kxx>0 的图象与直线 y=x−1 交于点 A3,m.
(1)求 k 的值;
(2)已知点 Pn,0n>0,过点 P 作垂直于 x 轴的直线,交直线 y=x−1 于点 B,交函数 y=kxx>0 于点 C.
①当 n=4 时,判断线段 PC 与 BC 的数量关系,并说明理由;
②若 PC≤BC,结合图象,直接写出 n 的取值范围.
23. 如图,在 △ABC 中,∠ACB=90∘,以 BC 为直径的 ⊙O 交 AB 于点 D,E 是 AC 中点,连接 DE.
(1)判断 DE 与 ⊙O 的位置关系并说明理由;
(2)设 CD 与 OE 的交点为 F,若 AB=10,BC=6,求 OF 的长.
24. GDP 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止 2020 年 4 月 27 日,对除西藏外的 30 个省区市第一季度有关 GDP 的数据进行收集、整理、描述和分析.下面给出了部分信息:
a.各省区市 GDP 数据的频数分布直方图,如图 1(数据分成 6 组,各组是 0
c.30 个省区市 2020 年第一季度及 2019 年 GDP 增速排名统计图,如图 2:
d.北京 2020 年第一季度 GDP 数据约为 7.5 千亿,GDP 增速排名为第 22.
根据以上信息,回答下列问题.
(1)在 30 个省区市中,北京 2020 年第一季度 GDP 的数据排名第 .
(2)在 30 个省区市 2020 年第一季度及 2019 年 GDP 增速排名统计图中,请在图中用“○”圈出代表北京的点.
(3)2020 年第一季度 GDP 增速排名位于北京之后的几个省份中,2019 年 GDP 增速排名的最好成绩是第 .
(4)下列推断合理的是 .
①与 2019 年 GDP 增速排名相比,在疫情冲击下,2020 年全国第一季度增速排名,部分省市有较大下滑,如 D 代表的湖北排名下滑最多;
② A,B,C 分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于 2019 年 GDP 增速排名位置靠前.
25. 已知线段 AB=6 cm,点 M 是线段 AB 上一动点,以 AB 为直径作 ⊙O,点 C 的圆周上一点且 AC=4 cm.连接 CM,过点 A 作直线 CM 的垂线,交 ⊙O 于点 N,连接 CN,设线段 AM 的长为 x cm,线段 AN 的长为 y1 cm,线段 CN 的长为 y2 cm.
小华同学根据学习函数的经验,分别对函数 y1,y2,随自变量 x 的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
(1)按照下表中自变量 x 的值进行取点、画图、测量,分别得到了 y1,y2 与 x 的几组对应值:
请你补全表格的相关数值,保留两位小数.
(2)在同一平面直角坐标系 xOy 中,描出补全后的表中各组数值所对应的点 x,y1,x,y2,并画出函数 y1,y2 的图象(函数 y2 的图象如图,请你画出 y1 的图象).
(3)结合画出的函数图象,解决问题:当 △CAN 是等腰三角形时,AM 的长度约为 cm.
26. 在平面直角坐标系中,已知抛物线 y=ax2+2ax+c 与 x 轴交于点 A,B,且 AB=4.抛物线与 y 轴交于点 C,将点 C 向上移动 1 个单位得到点 D.
(1)求抛物线对称轴;
(2)求点 D 纵坐标(用含有 a 的代数式表示);
(3)已知点 P−4,4,若抛物线与线段 PD 只有一个公共点,求 a 的取值范围.
27. 点 C 为线段 AB 上一点,以 AC 为斜边作等腰 Rt△ADC,连接 BD,在 Rt△ABD 外侧,以 BD 为斜边作等腰 Rt△BED,连接 EC.
(1)如图 1,当 ∠DBA=30∘ 时:
①求证:AC=BD;
②判断线段 EC 与 EB 的数量关系,并证明;
(2)如图 2,当 0∘<∠DBA<45∘ 时,EC 与 EB 的数量关系是否保持不变?
对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:
想法 1:尝试将点 D 为旋转中心,过点 D 作线段 BD 垂线,交 BE 延长线于点 G,连接 CG;通过证明 △ADB≌△CDG 解决以上问题;
想法 2:尝试将点 D 为旋转中心,过点 D 作线段 AB 垂线,垂足为点 G,连接 EG.通过证明 △ADB∽△GDE 解决以上问题;
想法 3:尝试利用四点共圆,过点 D 作 AB 垂线段 DF,连接 EF,通过证明 D,F,B,E 四点共圆,利用圆的相关知识解决以上问题.
请你参考上面的想法,证明 EC=EB(一种方法即可).
28. 过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.
(1)如图,在等腰 Rt△ABC 中,∠A=90∘,AB=AC=2.
①在下图中画出一条 Rt△ABC 的形内弧;
②在 Rt△ABC 中,其形内弧的长度最长为 .
(2)在平面直角坐标系中,点 D−2,0,E2,0,F0,1.点 M 为 △DEF 形内弧所在圆的圆心.求点 M 纵坐标 yM 的取值范围;
(3)在平面直角坐标系中,点 M2,23,点 G 为 x 轴上一点,点 P 为 △OMG 最长形内弧所在圆的圆心,求点 P 纵坐标 yP 的取值范围.
答案
第一部分
1. C
2. B
3. D
4. C
5. B
6. A
7. B
8. C
第二部分
9. −1
10. 3.1
11. −5,1
12. a+b2=a2+2ab+b2
13. 8
14. S2
15. x2+62=20−x2
16. 同圆或等圆半径相等,三边相等的三角形是等边三角形,等边三角形的内角是 60∘,一条弧所对的圆周角是它所对圆心角的一半(直径所对的圆周角是直角,正弦定义,三角函数值)
第三部分
17. 18−15−1+4sin30∘+2−1=32−5+4×12+2−1=42−4.
18.
3x+1<2x, ⋯⋯①x−12
3x+3<2x.
得
x<−3.
解不等式 ②:
x−1<2x+4.
得
x>−5.
不等式组的解集是
−5
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠ABD=∠BDE.
∴∠CBD=∠BDE.
∴EB=ED.
∵F 是 BD 中点,
∴EF 平分 ∠BED.
20. (1) 当 k=1 时,此方程为 x2−4x+3=0,
x−1x−3=0,x1=1,x2=3.
(2) 由题意得 k≠0,Δ=16−12k>0.
∴k<43.
∴k<43 且 k≠0.
21. (1) ∵CE=CD,CF=CB,
∴ 四边形 DBEF 是平行四边形,DE=2CD,BF=2BC.
∵ 菱形 ABCD 中,CD=CB.
∴DE=BF.
∴ 四边形 DBEF 是矩形.
(2) ∵AB=5,
∴BF=10.
∵ 菱形 ABCD 中,cs∠ABD=35,∠DBF=∠ABD.
∴cs∠DBF=35.
∵∠BDF=90∘,
∴DB=6.
∴DF=8.
22. (1) 把 x=3 代入 y=x−1 得 y=2.
∴A3,2.
又 y=kxx>0 图象过点 A3,2,解得 k=6.
(2) ① PC=BC.
当 n=4 时,B4,3,C4,32,
PC=32,BC=32.
② 0
连接 OD,CD,OE.
∵BC 为 ⊙O 的直径.
∴∠CDA=∠CDB=90∘.
∵E 是 AC 中点,
∴ED=EC.
∵OC=OD,OE=OE,
∴△OCE≌△ODE.
∴∠ODE=∠OCE=90∘.
∴OD⊥DE.
∴DE 与 ⊙O 相切.
(2) ∵∠ACB=90∘,AB=10,BC=6,
∴AC=8,CE=4,OC=3.
∵DE,CE 与 ⊙O 相切,
∴DE=CE,∠CEO=∠DEO.
∴OE⊥CD.
∴OE=5.
∵OC⋅CE=OE⋅CF.
∴CF=125.
∴OF=95.
24. (1) 11
(2) 如图.
(3) 8
(4) ①②
25. (1) 5.48
【解析】
(2)
(3) 2.98 cm 或 1.50
26. (1) 对称轴 x=−2a2a=−1.
(2) ∵AB=4,A−3,0,B1,0,
把 1,0 代入表达式:a+2a+c=0 得:c=−3a.
∴C0,−3a.
∴D0,−3a+1,yD=−3a+1.
(3) 当 a>0 时,将点 P−4,4 代入抛物线 y=ax2+2ax−3a 得:
4=16a−8a−3a,a=45.
∴ 当 a≥45 时,抛物线与线段 PD 只有一个交点;
当 a<0 时,抛物线的顶点为 −1,−4a,
当 −4a=4 时,a=−1.
综上所述,当 a≥45 或 a=−1 时,抛物线与线段 PD 只有一个交点.
27. (1) ①过点 D 作 DF⊥AC 于 F.
∵∠DBA=30∘,
∴DF=12BD.
∵ 以 AC 为斜边作等腰 Rt△ADC,
∴AF=FC.
∴DF=12AC.
∴AC=BD.
② ∵ 等腰 Rt△ADC 与等腰 Rt△BED 中,AC=BD,
∴DC=DE,∠FDC=∠CDE=45∘.
∵∠DBA=30∘,
∴∠FDB=60∘,∠CDB=15∘.
∴∠CDE=60∘.
∴△CDE 是等边三角形.
∵EB=DE,
∴EC=EB.
(2) 法 1.添加辅助线.
证出 △ADB≌△CDG.
∴∠DCG=∠A=45∘.
∴∠GCB=90∘.
∵EG=EB,
∴EC=EB.
【解析】法 2.添加辅助线.
证出 △ADB∽△GDE.
∴∠DGE=∠A=45∘.
∴GE 平分 ∠DGC.
∴GE 是 DC 的中垂线.
∴ED=EC=EB.
法 3.添加辅助线.
证出 ∠EFB=∠EDB=45∘.
∴FE 是 DC 的中垂线,
∴ED=EC=EB.
28. (1) ①如图所示.
② π
【解析】①如图所示.
②当 OB=2 时,Rt△ABC 的形内弧最长,此时弧长 =π.
(2) 当圆心在 x 轴下方时,此时最长形内弧与线段 DF,EF 相切,
∵△DOF∽△DOM1,
∴OF⋅OM1=OD2.
∴OM1=4.
∴yM≤−4;
当圆心在 x 轴上方时,此时最长形内弧与 x 轴相切,
∵△EGM2∽△HEG,
∴HG⋅HM2=HE2.
∴EH=52.
∴EM2=52.
∴yM≥52.
综上所述,yM≤−4 或 yM≥52.
(3) 当 xG≤−4 时,此时最长形内弧与 x 轴相切,
∵△GOP1∽△GHO,
∴GP1=43.
∴yP1≥43;
当 −4
当 0
当 xG≥4 时,此时最长形内弧与线段 MG 相切,
解得 yP4≤−233.
综上所述,yP≥433 或 yP≤−233.
2023年北京市房山区中考数学二模试卷(含解析): 这是一份2023年北京市房山区中考数学二模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年北京市房山区中考数学二模试卷(含解析): 这是一份2023年北京市房山区中考数学二模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年北京市房山区中考二模数学试卷(无答案): 这是一份2023年北京市房山区中考二模数学试卷(无答案),共7页。试卷主要包含了单选题,未知,填空题等内容,欢迎下载使用。












