2020年北京市石景山区中考二模数学试卷

这是一份2020年北京市石景山区中考二模数学试卷，共15页。试卷主要包含了选择题，填空题，小器一容三斛；大器一，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 如图，用量角器度量 ∠AOB，可以读出 ∠AOB 的度数为
A. 30∘B. 60∘C. 120∘D. 150∘

2. 花粉的质量很小，一粒某种植物花粉的质量约为 0.000032 毫克，将 0.000032 用科学记数法表示应为
A. 3.2×105B. 3.2×10−5C. 3.2×10−4D. 32×10−6

3. 如图是某个几何体的三视图，则该几何体是
A. 圆锥B. 长方体C. 三棱柱D. 圆柱

4. 实数 m，n 在数轴上的对应点的位置如图所示，则正确的结论是
A. m>nB. m>−n
C. m>nD. mn>0

5. 如图，小石同学在正方形网格图中建立平面直角坐标系后，点 A 的坐标为 −1,1，点 B 的坐标为 2,0，则点 C 的坐标为
A. 1,−2B. −2,1C. −1,−2D. 1,−1

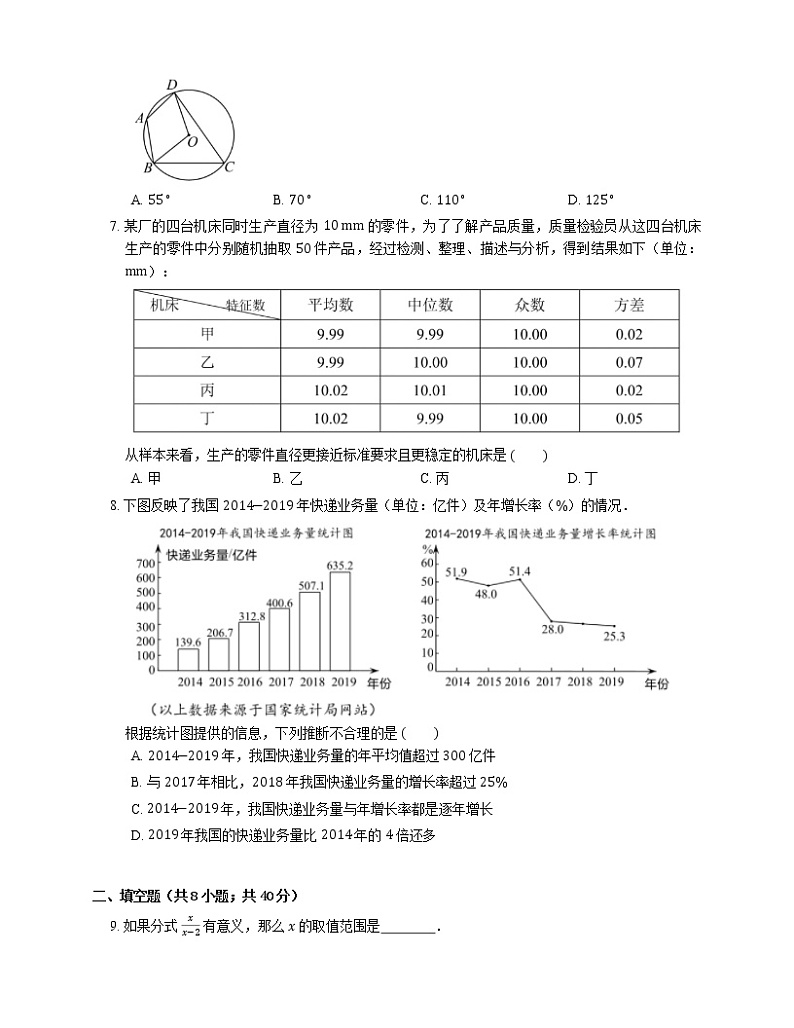
6. 如图，四边形 ABCD 是 ⊙O 的内接四边形，∠A=125∘，则 ∠BOD 的度数为
A. 55∘B. 70∘C. 110∘D. 125∘

7. 某厂的四台机床同时生产直径为 10 mm 的零件，为了了解产品质量，质量检验员从这四台机床生产的零件中分别随机抽取 50 件产品，经过检测、整理、描述与分析，得到结果如下（单位：mm）：
从样本来看，生产的零件直径更接近标准要求且更稳定的机床是
A. 甲B. 乙C. 丙D. 丁

8. 下图反映了我国 2014−2019 年快递业务量（单位：亿件）及年增长率（%）的情况．
根据统计图提供的信息，下列推断不合理的是
A. 2014−2019 年，我国快递业务量的年平均值超过 300 亿件
B. 与 2017 年相比，2018 年我国快递业务量的增长率超过 25%
C. 2014−2019 年，我国快递业务量与年增长率都是逐年增长
D. 2019 年我国的快递业务量比 2014 年的 4 倍还多

二、填空题（共8小题；共40分）
9. 如果分式 xx−2 有意义，那么 x 的取值范围是 ．

10. 如果 x2+3x=2020，那么代数式 x2x+1−x−12 的值为 ．

11. 如图，AB 是 ⊙O 的直径，点 C 是 ⊙O 上一点，OA=3，∠OCA=40∘，则阴影部分的面积为 ．

12. 如图 1，边长为 a 的大正方形中有一个边长为 b 的小正方形，若将图 1 中的阴影部分拼成一个矩形如图 2，比较两图中阴影部分的面积，写出一个正确的等式： ．

13. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中第七卷《盈不足》记载了一道有趣的数学问题：
“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何?”
译文：“今有大容器 5 个，小容器 1 个，总容量为 3 斛；大容器 1 个，小容器 5 个，总容量为 2 斛．问大容器、小容器的容积各是多少斛?”
设大容器的容积为 x 斛，小容器的容积为 y 斛，根据题意，可列方程组为 ．

14. 某种黄豆在相同条件下的发芽试验，结果如表所示：
试验粒数n5001000200040007000100001200015000发芽的粒数m42186817143456602085801030812915发芽的频率
估计该种黄豆发芽的概率为 （精确到 0.01）．

15. 在平面直角坐标系 xOy 中，点 A 的坐标为 −1,2，点 B 的坐标为 m,2，若直线 y=x−1 与线段 AB 有公共点，则 m 的值可以为 （写出一个即可）．

16. 正方形 ABCD 中，点 E 在边 AB 上，EA=1，EB=2，将线段 DE 绕点 D 逆时针旋转，使点 E 落在直线 BC 上的点 F 处，则 FB 的长度为 ．

三、解答题（共12小题；共156分）
17. 计算：∣2−2∣+4cs45∘+18−12−1．

18. 解不等式组 2x−8≤0,x−1>5x+42.

19. 关于 x 的一元二次方程 x2−k+3x+k+2=0．
（1）求证：方程总有两个实数根；
（2）若方程有一个根为负数，求 k 的取值范围．

20. 如图，在四边形 ABCD 中，AD∥BC，AD=DC，DE 平分 ∠ADC 交 BC 于点 E，连接 AE．
（1）求证：四边形 AECD 是菱形；
（2）连接 AC 交 DE 于点 F．若 ∠ABC=90∘，AC=23，CE=2，求 AB 的长．

21. 在抗击新冠肺炎疫情期间，老百姓越来越依赖电商渠道获取必要的生活资料．小石经营的水果店也适时加入了某电商平台，并对销售的水果中的部分（如下表）进行促销：参与促销的水果免配送费且一次购买水果的总价满 128 元减 x 元．每笔订单顾客网上支付成功后，小石会得到支付款的 80%．
（1）当 x=8 时，某顾客一次购买苹果和车厘子各 1 箱，需要支付 元，小石会得到 元；
（2）在促销活动中，为保障小石每笔订单所得到的金额不低于促销前总价的七折，则 x 的最大值为 ．

22. 如图，在平面直角坐标系 xOy 中，函数 y=mxx>0 的图象 G 经过点 A3,1，直线 y=x−2 与 x 轴交于点 B．
（1）求 m 的值及点 B 的坐标；
（2）直线 y=kxk≠0 与函数 y=mxx>0 的图象 G 交于点 C，记图象 G 在点 A，C 之间的部分与线段 OC，OB，BA 围成的区域（不含边界）为 W．
①当 k=1 时，直接写出区域 W 内的整点个数；
②若区域 W 内恰有 2 个整点，结合函数图象，求 k 的取值范围．

23. 如图，点 A，B，C 在 ⊙O 上，D 是弦 AB 的中点，点 E 在 AB 的延长线上，连接 OC，OD，CE，∠CED+∠COD=180∘．
（1）求证：CE 是 ⊙O 切线；
（2）连接 OB，若 OB∥CE，tan∠CEB=2，OD=4，求 CE 的长．

24. 经过多方努力，北京市 2019 年在区域空气质量同步改善、气象条件较常年整体有利的情况下，大气环境中细颗粒物（PM2.5）等四项主要污染物同比均明显改善．对北京市空气质量的有关数据进行收集、整理、描述与分析，下面给出了部分信息：
a．北京市 2019 年空气质量各级别分布情况如下图（全年无严重污染日）（不完整）：
b．北京市 2019 年大气环境中二氧化硫（SO2）的年均浓度为 4 微克/立方米，稳定达到国家二级标准（60 微克/立方米；PM10，二氧化氮（NO2）的年均浓度分别为 68 微克/立方米，37 微克/立方米，均首次达到国家二级标准（ 70 微克/立方米，40 微克/立方米）；PM2.5 的年均浓度为 m 微克/立方米，仍是北京市大气主要污染物，超过国家二级标准（35 微克/立方米）的 20%．
c．北京市 2019 年大气环境中 PM2.5 月均浓度变化情况如下：
二氧化硫（SO2）月均浓度（单位：微克/立方米）如下（不完整）：
月份123456789101112月均浓度9654323354
（以上数据来源于北京市生态环境局官方网站）
根据以上信息，回答下列问题：
（1）北京市 2019 年空气质量为“轻度污染”天数为
A．82 B．92 C．102
（2）m 的值是 ；
（3）北京市 2019 年大气环境中 PM2.5 月均浓度达到国家二级标准的概率为 ；
（4）北京市 2019 年大气环境中 SO2 月均浓度的众数是 4，则中位数是 ．

25. 如图，Q 是 AB 与弦 AB 所围成图形的外部的一定点，P 是弦 AB 上的一动点，连接 PQ 交 AB 于点 C．已知 AB=6 cm，设 P，A 两点间的距离为 x cm，P，C 两点间的距离为 y1 cm，Q，C 两点间的距离为 y2 cm．
小石根据学习函数的经验，分别对函数 y1，y2 随自变量 x 的变化而变化的规律进行了探究，下面是小石的探究过程，请补充完整：
（1）按照下表中自变量 x 的值进行取点、画图、测量，分别得到了 y1，y2 与 x 的几组对应值：
x/cm0123455.
（2）在同一平面直角坐标系 xOy 中，描出补全后的表中各组数值所对应的点 x,y1，x,y2，并画出函数 y1，y2 的图象；
（3）结合函数图象，解决问题：当 C 为 PQ 的中点时，PA 的长度约为 cm．

26. 在平面直角坐标系 xOy 中，抛物线 y=ax2+bx+3aa≠0 与 y 轴交于点 A，与 x 轴交于点 B，C（点 B 在点 C 左侧）．直线 y=−x+3 与抛物线的对称轴交于点 Dm,1．
（1）求抛物线的对称轴；
（2）直接写出点 C 的坐标；
（3）点 M 与点 A 关于抛物线的对称轴对称，过点 M 作 x 轴的垂线 l 与直线 AC 交于点 N，若 MN≥4，结合函数图象，求 a 的取值范围．

27. 在 △ABC 中，AB=AC，D 是边 BC 上的一点（不与点 B 重合），边 BC 上点 E 在点 D 的右边且 ∠DAE=12∠BAC，点 D 关于直线 AE 的对称点为 F，连接 CF．
（1）如图 1，
①依题意补全图 1；
②求证：CF=BD；
（2）如图 2，∠BAC=90∘，用等式表示线段 DE，CE，CF 之间的数量关系，并证明．

28. 对于平面直角坐标系 xOy 中的图形 M，N，给出如下定义：P 为图形 M 上任意一点，Q 为图形 N 上任意一点，如果线段 PQ 的长度有最小值，那么称这个最小值为图形 M，N 的“近距”，记作 d1M,N；如果线段 PQ 的长度有最大值，那么称这个最大值为图形 M，N 的“远距”，记作 d2M,N．已知点 A0,3，B4,3．
（1）d1（点 O，线段 AB）= ，d2（点 O，线段 AB）= ；
（2）一次函数 y=kx+5k>0 的图象与 x 轴交于点 C，与 y 轴交于点 D，若 d1（线段 CD，线段 AB）=2．
①求 k 的值：
②直接写出 d2（线段 CD，线段 AB）= ；
（3）⊙T 的圆心为 Tt,0，半径为 1．若 d1（⊙T，线段 AB）≤4，请直接写出 d2（⊙T，线段 AB）的取值范围．
答案
第一部分
1. C
2. B
3. D
4. B
5. A
6. C
7. A
8. C
第二部分
9. x≠2
10. 2019
11. 2π
12. a2−b2=a+ba−b
13. 5x+y=3,x+5y=2
14. 0.86
15. 答案不唯一，如：4m≥3
16. 2 或 4
第三部分
17. 原式=2−2+4×22+32−2=42.
18. 原不等式组为
2x−8≤0, ⋯⋯①x−1>5x+42. ⋯⋯②
解不等式 ①，得
x≤4.
解不等式 ②，得
x