2019年天津市南开区中考二模数学试卷

这是一份2019年天津市南开区中考二模数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 计算 2−(−3)×4 的结果是 ( )
A. 10B. −20C. −10D. 14

2. 2cs30∘ 的值等于 ( )
A. 3B. 32C. 233D. 1

3. 我区围绕培育和践行社会主义核心价值观为主线，扎实推进《 天津市文明行为促进条例》宣传贯彻，与《天津日报》联合刊发《文明南开 社区读本》文明条例宣传专刊 40000 份，将“40000 用科学记数法表示为 ( )
A. 4×105B. 4×104C. 0.4×105D. 40×103

4. 观察如图图形，是轴对称图形但不是中心对称图形的有 ( )
A. 1 个B. 2 个C. 3 个D. 4 个

5. 如图是一个由 5 个相同的正方体组成的立体图形，它的三视图是 ( )
A. B.
C. D.

6. 实数 a，b，c，d 在数轴上的对应点的位置如图所示，在这四个数中，绝对值最小的数是 ( )
A. aB. bC. cD. d

7. 方程组 3x+4y=16,5x−6y=33 的解是 ( )
A. x=6,y=−12B. x=9,y=2C. x=4,y=1D. x=5,y=−2

8. 反比例函数 y=2x 的图象上有两点 A(x1,y1)，B(x2,y2)，若 x1>x2，x1x2>0，则 y1−y2 的值是 ( )
A. 正数B. 0C. 负数D. 非负数

9. 如图，在 Rt△ABC 中，∠BAC=90∘，AB=AC，将 △ABC 绕点 C 顺时针旋转 40∘ 得到 △AʹBʹC，CBʹ 与 AB 相交宇点 D，连接 AAʹ，则 ∠BʹAʹA 的度数为 ( )
A. 10∘B. 15∘C. 20∘D. 30∘

10. 如图所示的“六芒星”图标是由圆的六等分点连接而成，若圆的半径为 2，则图中阴影部分的面积为 ( )
A. 3B. 33C. 6D. 43

11. 如图，正 △ABC 的边长为 2，过点 B 的直线 l⊥AB，且 △ABC 与 △AʹBCʹ 关于直线 l 对称，D 为线段 BCʹ 上一动点，则 AD+CD 的最小值是 ( )
A. 3B. 2C. 32D. 4

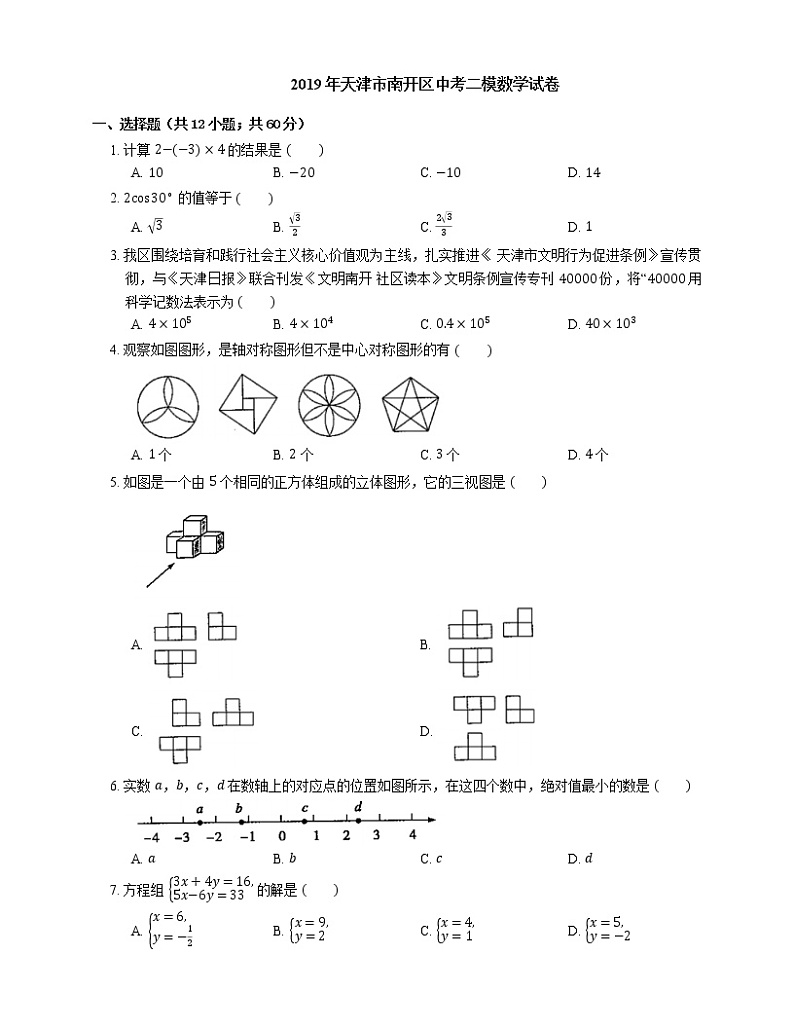
12. 如图，已知二次函数 y=ax2+bx+c(a≠0) 的图象与 x（a 不等于 0）的图象与 x 轴交于点 A(−1,0)，顶点坐标为 (1,n)，与 y 轴的交点在 (0,2) 和 (0,3) 之间（不包括端点）．有下列结论：①当 x>3 时，y<0；② n=c−a；③ 3a+b>0；④ −1A. 1 个B. 2 个C. 3 个D. 4 个

二、填空题（共5小题；共25分）
13. 计算 (−3a)2⋅a3= ．

14. 计算 xx−2−xx+2÷4x2−x 的结果等于 ．

15. 已知直线 y=kx+1 经过第一、二、四象限，该直线解析式可以是 ．

16. 如图，在圆形靶中，AC 与 BD 是 ⊙O 的两条直径，首尾顺次连接点 A，B，C，D，得到四边形 ABCD，若 ∠BAC=30∘，则射击到靶中阴影部分的概率是 ．

17. 如图，已知正方形 ABCD 的边长为 5，点 E，F 分别在 AD，DC 上，AE=DF=2，BE 与 AF 相交于点 G，点 H 为 BF 的中点，连接 GH，则 GH 的长为 ．

三、解答题（共8小题；共104分）
18. 如图，在边长都是 1 的小正方形组成的网格中，A，B，C，D 均为格点，线段 AB，CD 相交于点 O．
（1）线段 CD 的长等于 ；
（2）请你借助网格，使用无刻度的直尺画出以 A 为一个顶点的矩形 ARST，满足点 O 为其对角线的交点，并简要说明这个矩形是怎么画的（不要求证明） ．

19. 解不等式组 2x−1<5, ⋯⋯①3x+12−1≥x. ⋯⋯② 请结合题意填空，完成本题的解答：
（1）解不等式 ①，得 ；
（2）解不等式 ②，得 ；
（3）把不等式 ① 和 ② 的解集在数轴上表示出来：
（4）原不等式组的解集为 ．

20. 在某中学举行的一次知识竞赛活动中，每个班参加竞赛的人数都相同．成绩分别为 A，B，C，D 四个等级，四个等级对应的分数依次为 100 分，90 分，80 分，70 分，现将九年级一班和二班的成绩整理并绘制出如图的统计图．
请根据以上提供的信息，解答下列问题：
（1）每个班参加竞赛的学生人数为 ；
（2）二班成绩为 B 等级的学生占比赛人数的 m%，则 m= ；
（3）求一班参加竞赛学生成绩的平均数；
（4）求二班参加竞赛学生成绩的众数和中位数．

21. 已知 OA，OB 是 ⊙O 的半径，且 OA⊥OB，点 P 是射线 OA 上的一点（点 A 除外），直线 BP 交 ⊙O 于点 Q，过 Q 作 ⊙O 的切线交射线 OA 于点 E．
（1）如图 ①，点 P 在线段 OA 上，若 ∠AQE=28∘，求 ∠OBQ 的大小；
（2）如图 ②，点 P 在 OA 的延长线上，若 ∠AQE=28∘，求 ∠OBQ 的大小．

22. 在一次海上救援中，两艘专业救助船 A，B 同时收到有关可疑漂浮物的讯息，可疑漂浮物 P 在救助船 A 的北偏西 36.8∘ 方向上，在救助船 B 的西南方向上，船 B 在船 A 正北方向 150 海里处．（参考数据：sin36.8∘≈0.6，cs36.8∘≈0.8，tan36.8∘≈0.75，结果保留整数）
（1）求可疑漂浮物 P 到 A，B 两船所在直线的距离；
（2）若救助船 A，B 分别以 40 海里/时，30 海里/时的速度同时出发，匀速直线前往 P 处搜救，试通过计算判断哪艘船先到达 P 处．

23. 甲、乙两家商场平时以同样价格出售相同的商品．“五一”节期间两家商场都让利酬宾，在甲商场按累计购物金额的 85% 收费；在乙商场累计购物金额超过 400 元后，超出 400 元的部分按 75% 收费，设小红在同一商场累计购物金额为 x 元，其中 x>400．
（1）根据题意，填写下表（单位：元）：
累计购物实际花费500700⋯x在甲商场425⋯在乙商场625⋯
（2）当 x 取何值时，小红在甲、乙两商场的实际花费相同?
（3）“五一”节期间，小红如何选择这两家商场去购物更省钱?

24. 如图 1，已知平行四边形 ABCD，AB∥x 轴，AB=6，点 A 的坐标为 (1,−4)，点 D 的坐标为 (−3,4)，点 B 在第四象限，点 P 是平行四边形 ABCD 边上的一个动点．
（1）若点 P 在边 BC 上，PD=CD，求点 P 的坐标；
（2）若点 P 在 AB，AD 上，点 P 关于坐标轴对称的点 Q 落在直线 y=x−1 上，求点 P 的坐标；
（3）若点 P 在 CD 上，点 G 是 AD 与 y 轴的交点，如图 2，过点 P 作 y 轴的平行线 PM，过点 G 作 x 轴的平行线 GM，它们相交于点 M，将 △PGM 沿直线 PG 翻折，当点 M 的对应点落在坐标轴上时，求点 P 的坐标（直接写出答案）．

25. 如图所示，Rt△ABO 的两直角边 OA，OB 分别在 x 轴的负半轴和 y 轴的正半轴上，O 为坐标原点，A，B 两点的坐标分别为 (−3,0)，(0,4)，抛物线 y=12x2+bx+c 经过点 B，且顶点在直线 x=3 上．
（1）求抛物线对应的函数关系式；
（2）若把 △ABO 沿 x 轴向右平移得到 △DCE，点 A，B，O 的对应点分别是 D，C，E，当四边形 ABCD 是菱形时，试判断点 C 和点 D 是否在该抛物线上，并说明理由；
（3）在（Ⅱ）的条件下，连接 BD．已知在对称轴上存在一点 P，使得 △PBD 的周长最小．若点 M 是线段 OB 上的一个动点（点 M 与点 O，B 不重合），过点 M 作 MN∥BD 交 x 轴于点 N，连接 PM，PN，设 OM 的长为 t，△PMN 的面积为 S，求 S 与 t 的函数关系式，并写出自变量 t 的取值范围．S 是否存在最大值?若存在，求出最大值和此时 M 点的坐标；若不存在，请说明理由．
答案
第一部分
1. D
2. A
3. B
4. B
5. A
6. C【解析】由图可知：c 到原点的距离最近，
∴ 在这四个数中，绝对值最小的数是 c．
7. A【解析】3x+4y=16, ⋯⋯①5x−6y=33, ⋯⋯②
①×3 得：9x+12y=48, ⋯⋯③
②×2 得：10x−12y=66, ⋯⋯④
③+④ 得：19x=114，
解得：x=6，
将 x=6 代入 ①，解得：y=−12，
故方程组的解为：x=6,y=−12.
8. C【解析】反比例函数 y=2x 的图象位于一、三象限，且在每一象限内 y 随 x 的增大而减小，
∵x1x2>0，
∴x1，x2 同号，即点 A，B 在同一象限，
∵x1>x2，
∴y2>y1，
∴y1−y2<0．
9. C【解析】由旋转可知：∠ACAʹ=40∘，AC=AʹC，∠BʹAʹC=∠BAC=90∘，
∴∠CAAʹ=∠AAʹC=12(180∘−40∘)=70∘，
∴∠BʹAʹA=90∘−70∘=20∘．
10. D
【解析】如图所示，
由“六芒星”的特殊性易知图中所有的三角形均为全等的等边三角形，圆的半径为 2，即 OB=2，
∴BD=1，AB=BDcs30∘=233，
∴S△ABC=34×2332=33，
∴S阴影=33×12=43．
11. D【解析】连接 CCʹ，如图所示：
∵△ABC，△AʹBCʹ 均为正三角形，
∴∠ABC=∠Aʹ=60∘，AʹB=BC=AʹCʹ，
∴AʹCʹ∥BC，
∴ 四边形 AʹBCCʹ 为菱形，
∴ 点 C 关于 BCʹ 对称的点是 Aʹ，即 CD=AʹD，
∴ 当点 D 与点 B 重合时，AD+CD 取最小值，
此时 AD+CD=2+2=4．
12. C【解析】因为函数图象与 x 轴交于点 A(−1,0)，且对称轴为 x=1，则函数图象与 x 轴的另一个交点为 (3,0)，所以当 x>3 时，y<0，故①正确；
因为抛物线的对称轴为 x=−b2a=1，所以 b=−2a，
因为顶点坐标为 (1,n)，所以 n=a+b+c=a−2a+c，即 n=c−a，故②正确；
因为抛物线开口向下，所以 a<0，
因为 b=−2a，所以 3a+b=3a−2a=a<0，故③错误；
因为函数图象过点 (−1,0)，即 x=−1 时，y=0，所以 a−b+c=0，
因为 b=−2a，所以 a+2a+c=0，即 c=−3a，
所以抛物线与 y 轴的交点在 (0,2) 和 (0,3) 之间（不包括端点），
所以 2综上，①②④正确．
第二部分
13. 9a5
14. 1−x−2
15. y=−x+1（答案不唯一）
16. 13
17. 342
【解析】∵ 四边形 ABCD 为正方形，
∴∠BAE=∠D=90∘，AB=AD，
在 △ABE 和 △DAF 中，
∵AB=AD,∠BAE=∠ADF,AE=DF,
∴△ABE≌△DAF(SAS)，
∴∠ABE=∠DAF，
∵∠ABE+∠BEA=90∘，
∴∠DAF+∠BEA=90∘，
∴∠AGE=∠BGF=90∘，△BGF 为直角三角形，
∵ 点 H 为 BF 的中点，
∴GH=12BF，
∵BC=5，CF=CD−DF=5−2=3，
∴BF=BC2+CF2=34，
∴GH=12BF=342．
第三部分
18. （1） 17
【解析】CD=42+12=17．
（2） 取格点 P，Q，K，H，J，M，延长 AB 至 H，连接 PQ 交网格于 I，连接 KD 交网格于 N，连接 IJ 交 AH 于 S，连接 MN 交 AJ 于 R，连接 RO 并延长交网格于点 T，连接 AR，RS，ST，TA，则四边形 ARST 即为所求矩形
【解析】因为 BE=12，GF=14，
所以 AF=74，BEAF=BOAO=1274=27，
所以 AO=79AB，BO=29AB，
根据矩形的对角线互相平分，
所以需要在 AH 上取 S 点使得 OS=OA，
所以 BS=59AB，
又因为 BH=AB，则只需 HSBS=45 即可，取 PQ 交格点为 I，再取 J 并连接 BJ，IJ 交 AH 于点 S 使得 △HJS∽△BIS，且 HJBI=HSBS=22.5=45，因此 OS=OA；
作 OW⊥AR，
因为 AO=79AB，
所以 AW=79AG=149，WG=2−149=49，
所以需要在 AR 上取 R 使得 GR=109，从而使得 RW=WA，
因为 GJ=2，所以只需 JRGR=45 即可，
所以取 KD 交格点与 N，再取格点 M，连接 MN 交 AJ 于点 R，则 OA=OR=OS，
所以 ∠SRA=90∘，延长 RO 交网格于 T，则 SR∥TA，四边形 TARS 是矩形．
19. （1） x<3
（2） x≥1
（3）
（4） 1≤x<3
20. （1） 20
【解析】每个班参加竞赛的学生人数为：5+10+2+3=20（人）．
（2） 10
【解析】B 等级的学所占百分比为：1−35%−30%−25%=10%，故 m=10．
（3） 一班参加竞赛学生成绩的平均数 x=100×5+90×10+80×2+70×320=88.5（分）．
（4） ∵ 二班参加竞赛学生成绩，A 等级所占百分比最大，
∴ 众数是 100；
由 A 等级占 35%，B 等级占 10%，C 等级占 30% 可知中位数是 80．
21. （1） 如图 ①, 连接 OQ，
∵OA⊥OB，QE 是 ⊙O 的切线，
∴∠AOB=90∘，∠OQE=90∘，
∴∠AQB=45∘，
∵∠AQE=28∘，
∴∠OQB=∠OQE−∠AQB−∠AQE=90∘−45∘−28∘=17∘，
∵OQ=OB，
∴∠OBQ=∠OQB=17∘．
（2） 如图 ②，连接 OQ，
∵∠AQE=28∘，
∴∠OQA=90∘−28∘=62∘，
∵OQ=OA，
∴∠OQA=∠OAQ=62∘，
∵∠QOA=180∘−62∘−62∘=56∘，
∴∠BOQ=90∘−∠QOA=34∘，
∵OB=OQ，
∴∠OBQ=12(180∘−34∘)=73∘．
22. （1） 过点 P 作 PH⊥AB 交 AB 于点 H，
由题意可知：∠PAH=36.8∘，∠PBH=45∘，∠PHB=∠PHA=90∘，
∴tan∠PAH=PHAH≈0.75，
∴AH≈43PH，PH=BH，
∴AB=AH+BH≈43PH+PH=150，
∴PH≈64，
∴ 可疑漂浮物 P 到 A，B 两船所在直线的距离约为 64 海里．
（2） 由（Ⅰ）知 PH=64，
∴BP=PHsin45∘=2PH=642，
∴B 船到达 P 处所用时间 =642÷30≈3（小时），
∵sin∠PAH=PHAP≈0.6，
∴AP≈PH0.6=64÷35=3203，
∴A 船到达 P 处所用时间 =3203÷40=83（小时），
∵83<3，
∴A 船先到达 P 处．
答：A 船先到达 P 处．
23. （1） 700×0.85=595，在甲商场购买 x 元时，实际花费是 0.85x（元）；400+(500−400)×0.75=475，在乙商场购买 x 元时，实际花费是 400+(x−400)×0.75=0.75x+100；
填表如下：
累计购物500700⋯⋯x实际花费在甲商场425595⋯0.85x在乙商场475625⋯0.75x+100
（2） 根据题意得：0.85x=0.75x+100，解得：x=1000，
∴ 当 x=1000 时，小红在甲、乙两商场的实际花费相同．
（3） 由 0.85x<0.75x+100，解得：x<1000，由 0.85x>0.75x+100，解得：x>1000，
结合（2）可知：
当小红累计购物的金额大于 400 小于 1000 元时，在甲商场购物更省钱；
当小红累计购物的金额等于 1000 元时，在甲乙商场样省钱；
当小红累计购物的金额大于 1000 元时，在乙商场购物更省钱．
24. （1） ∵PD=CD，P 在边 BC 上，
∴ 点 P 与点 C 重合，
∵CD=6，
∴ 点 P 坐标为 (3,4)．
（2） ① 当点 P 在边 AD 上时，
∵A(1,−4)，D(−3,4)，
设直线 AD 的解析式为 y=kx+b，
则 −4=k+b,4=−3k+b, 解得 k=−2,b=−2,
∴ 直线 AD 的解析式为 y=−2x−2，
设 P(a,−2a−2)，且 −3≤a≤1，
若点 P 关于 x 轴的对称点 Q1(a,2a+2) 在直线 y=x−1 上，
则 2a+2=a−1，解得 a=−3，此时 P(−3,4)．
若点 P 关于 y 轴的对称点 Q2(−a,−2a−2) 在直线 y=x−1 上，
则 −2a−2=−a−1，解得 a=−1，此时 P(−1,0)；
② 当点 P 在边 AB 上时，设 P(a,−4) 且 1≤a≤7，
若点 P 关于 x 轴的对称点 Q3(a,4) 在直线 y=x−1 上，则 4=a−1，解得 a=5，此时 P(5,−4)，
若点 P 关于 y 轴的对称点 Q4(−a,−4) 在直线 y=x−1 上，则 −4=−a−1，解得 a=3，此时 P(3,−4)，
综上所述，点 P 的坐标为 (−3,4) 或 (−1,0) 或 (5,−4) 或 (3,−4)．
（3） 点 P 的坐标为 −655,4 或 P655,4．
【解析】由（Ⅱ）知直线 AD 的解析式为 y=−2x−2，
∴G(0,−2)，
如图，
当点 P 在线段 CD 上且在 y 轴左半侧时，设 P(m,4)(m<0)，
在 Rt△PNMʹ 中，
∵PM=PMʹ=6，PN=4，
∴NMʹ=PMʹ2−PN2=25，
在 Rt△OGMʹ 中，
∵OG2+OMʹ2=GMʹ2，
∴22+(25+m)2=m2，
解得 m=−655，
∴P−655,4，
当点 P 在 y 轴右半侧时，设 P(m,4)(m>0)，由上述解法解得 P655,4 也满足条件，
∴ 点 P 的坐标为 −655,4 或 P655,4．
25. （1） ∵ 抛物线 y=12x2+bx+c 的顶点在直线 x=3 上，
∴ 设该抛物线对应的函数关系式为：y=12(x−3)2+m．
将 B(0,4) 代入可得：4=92+m，
解得：m=−12，
∴ 该抛物线对应的函数关系式为：y=12(x−3)2−12=12x2−3x+4．
（2） 在 Rt△ABO 中，OA=3，OB=4，
∴AB=32+42=5．
当四边形 ABCD 是菱形时，BC=CD=DA=AB=5，
∴C(5,4)，D(2,0)．
当 x=5 时，y=12×52−3×5+4=32≠4，
当 x=2 时，y=12×22−3×2+4=0，
∴ 点 C 不在该抛物线上，点 D 在该抛物线上．
（3） 由（Ⅱ）可得，B(0,4)，D(2,0)，
由抛物线的对称性可知 B 点关于对称轴 x=3 的对称点 B′ 坐标为 (6,4)，
连接 B′D 交对称轴 x=3 于点 P，此时 △PBD 的周长最短，
设直线 B′D 的解析式为：y=kx+b，
则 0=2k+b,4=6k+b,
解得 k=1,b=−2,
∴ 直线 B′D 的解析式为：y=x−2．
当 x=3 时，y=3−2=1，
∴P(3,1)．
设对称轴交 x 轴于点 F，
∵MN∥BD，
∴△OMN∽△OBD．
∴OMOB=ONOD，即 t4=ON2．
∴ON=12t，NF=3−12t．
则
S△PMN=S梯形PFOM−S△PFN−S△OMN=(1+t)×32−12×3−12t×1−12×12t×t=−14t2+74t.
∴S=−14t2+74t(0 ∵a=−14<0，
∴ 抛物线开口向下，S 存在最大值．
S=−14t2+74t=−14t−722+4916．
∴ 当 t=72 时，S 取最大值 4916．
此时 M 点坐标为 0,72．