2019年江苏省无锡市滨湖区中考一模数学试卷

这是一份2019年江苏省无锡市滨湖区中考一模数学试卷，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 16 表示
A. 16 的平方根B. 16 的算术平方根
C. ±4D. ±2

2. 下列各式中，是 3x2y 的同类项的是
A. 3a2bB. −2xy2C. x2yD. 3xy

3. 据统计，2018 年无锡市商品房待售面积（报告期末已竣工的可供销售或出租的商品房屋建筑面积）约为 758 万平方米，这个数据用科学记数法可表示为
A. 758×104 m2B. 7.58×102 m2C. 7.58×104 m2D. 7.58×106 m2

4. 若 m>n，则下列各式中一定成立的是
A. m−2>n−2B. m−5−2nD. 4m<4n

5. 下列调查中，适宜采用全面调查（普查）的是
A. 对全国中学生心理健康现状的调查
B. 对冷饮市场上冰淇淋质量情况的调查
C. 对西安市市民实施低碳生活情况的调查
D. 对“神舟九号”飞船零部件状况的检查

6. 一几何体的三视图如图所示，这个几何体是
A. 四棱锥B. 圆锥C. 三棱柱D. 四棱柱

7. 给出下列 4 个命题：
①对顶角相等；
②同位角相等；
③在同一个圆中，同一条弦所对的圆周角都相等；
④圆的内接四边形对角互补．
其中，真命题为
A. ①②④B. ①③④C. ①④D. ①②③④

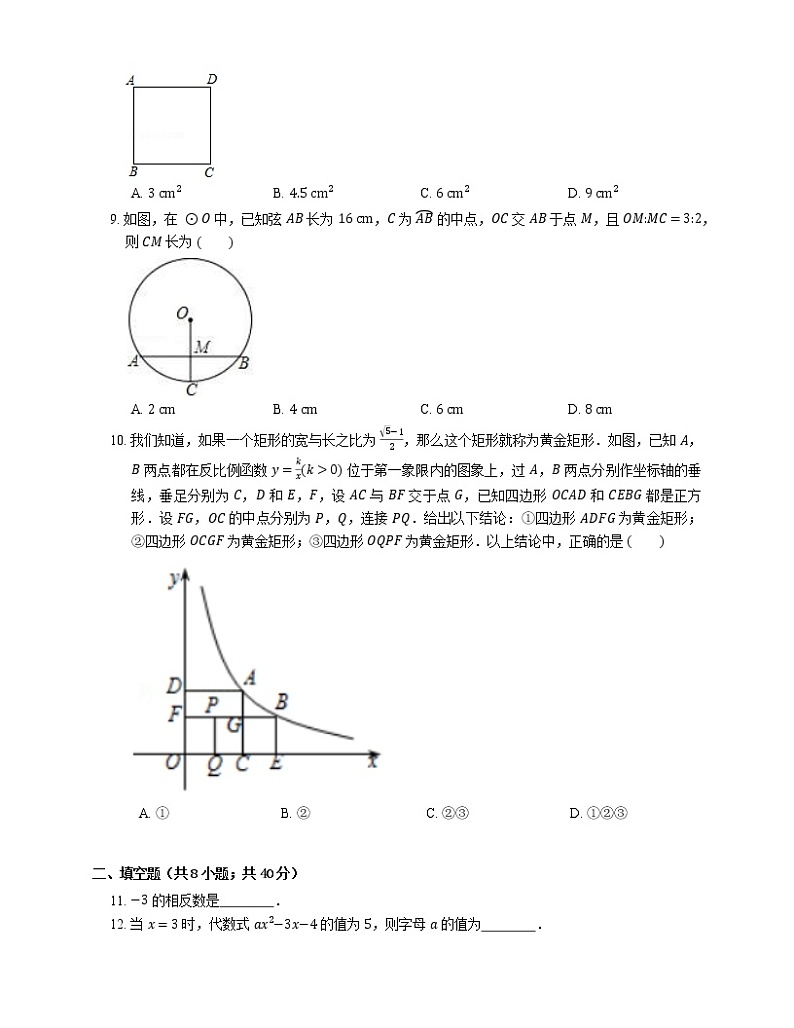
8. 如图，已知正方形 ABCD 的边长为 3 cm，若将这个正方形沿射线 AD 方向平移 2 cm，则平移前后图形的重叠部分的面积为
A. 3 cm2B. 4.5 cm2C. 6 cm2D. 9 cm2

9. 如图，在 ⊙O 中，已知弦 AB 长为 16 cm，C 为 AB 的中点，OC 交 AB 于点 M，且 OM:MC=3:2，则 CM 长为
A. 2 cmB. 4 cmC. 6 cmD. 8 cm

10. 我们知道，如果一个矩形的宽与长之比为 5−12，那么这个矩形就称为黄金矩形．如图，已知 A，B 两点都在反比例函数 y=kxk>0 位于第一象限内的图象上，过 A，B 两点分别作坐标轴的垂线，垂足分别为 C，D 和 E，F，设 AC 与 BF 交于点 G，已知四边形 OCAD 和 CEBG 都是正方形．设 FG，OC 的中点分别为 P，Q，连接 PQ．给出以下结论：①四边形 ADFG 为黄金矩形；②四边形 OCGF 为黄金矩形；③四边形 OQPF 为黄金矩形．以上结论中，正确的是
A. ①B. ②C. ②③D. ①②③

二、填空题（共8小题；共40分）
11. −3 的相反数是 ．

12. 当 x=3 时，代数式 ax2−3x−4 的值为 5，则字母 a 的值为 ．

13. 分解因式：x3−64x= ．

14. 函数 y=2x−4 中，自变量 x 的取值范围是 ．

15. 给出下列 4 种图形：①线段，②等腰三角形，③平行四边形，④圆．其中，不一定是轴对称图形的是 （填写序号）．

16. 如图，已知 a∥b，∠1=54∘，则 ∠2 的度数为 ．

17. 如图，已知 P 为等边 △ABC 形内一点，且 PA=3 cm，PB=4 cm，PC=5 cm，则图中 △PBC 的面积为 cm2．

18. 如图，已知 △ABC 中，∠BAC=90∘，AB=AC=6，D 为 BC 边一点，且 BD:DC=1:2，以 D 为一个顶点作正方形 DEFG，且 DE=BC，连接 AE，将正方形 DEFG 绕点 D 旋转一周，在整个旋转过程中，当 AE 取得最大值时 AG 的长为 ．

三、解答题（共10小题；共130分）
19. 回答下列问题．
（1）计算：−12−2+4⋅sin60∘−12；
（2）化简：xx−1−x+2x+1．

20. 请回答：
（1）解不等式：x3+x−12>1；
（2）解方程组：2x−y=5,3x+2y=4.

21. 如图所示，△ACB 和 △ECD 都是等腰直角三角形，∠ACB=∠ECD=90∘，D 为 AB 边上一点．
（1）求证：△ACE≌△BCD；
（2）若 AD=5，BD=12，求 DE 的长．

22. 为丰富同学们的校园生活，某校积极开展了形式多样的社团活动（每人仅限参加一项）．小明在八年级随机抽取了 2 个班级，对这 2 个班级参加体育类社团活动的人数进行了统计，并绘制了下面的统计图．已知这 2 个班级共有 6% 的学生参加“足球”项目，且参加“足球”项目的学生数占参加体育类社团活动学生数的 20%．
（1）这 2 个班参加体育类社团活动人数为 ．
（2）请在图中将表示“棒球”项目的图形补充完整；
（3）若该校八年级共有 600 名学生，请你根据上述信息估计该校八年级共有多少名学生参加“棒球”项目?

23. 某区招聘新教师即将进入面试环节，除了从外区抽调部分评委之外，还打算从本区教学专家库中每门学科再随机抽取 2 人，共同组成评委团队担任面试工作．已知该区初中数学学科专家库中共有 6 名候选人：杨老师（女）、王老师（男），陈老师（女）、周老师（男）、王老师（女）、李老师（女）．由于李老师（女）有直系亲属参加面试需回避，所以本区的 2 名初中数学学科评委只能在其余 5 人中随机产生．请用画树状图法或列表法等方式求出“所抽取的 2 名评委恰好是都是女教师”的概率．

24. 如图，已知矩形 OABC 的顶点 A 在 x 轴的负半轴上，顶点 C 在 y 轴上，且 AB=4．P 为 OC 上一点，将 △BCP 沿 PB 折叠，点 C 落在第三象限内点 Q 处，BQ 与 x 轴的交点 M 恰好为 OA 的中点，且 MQ=1．
（1）求点 A 的坐标；
（2）求折痕 PB 所对应的函数表达式．

25. 人生经常需要做“选择题”，比如“准备选择参加哪个社团”、“暑假打算去哪儿旅游”、“中考过后决定报考哪所学校”等等．下面就有一道“选择题”：李明家新买了一套房子，2020 年元旦准备乔迁入住．他家有辆车，关于车位，房地产开发商提供两种方案供业主选择：
（1）若采用租车位的方式，则每年共需缴费 元；
（2）现已知李明家手头的钱足够购买车位，但李明了解到，如果购买一种长期基金（一元起购，本金不可支取），每年可获得 6% 的固定收益（年终提取当年收益）．如果不考虑其他因素（如物价变化、租金变化、基金收益率变化等），根据以上信息，关于“租车位”或“买车位”哪种合算?请你帮助李明作出选择，并说明理由．

26. 如图 1，在 Rt△ABC 中，∠C=90∘，O 为斜边 AB 上一点，以 O 为圆心、 OA 为半径的圆恰好与 BC 相切于点 D，与 AB 的另一个交点为 E，连接 DE．
（1）请找出图中与 △ADE 相似的三角形，并说明理由；
（2）若 AC=3，AE=4，试求图中阴影部分的面积；
（3）小明在解题过程中思考这样一个问题：图 1 中的 ⊙O 的圆心究竟是怎么确定的呢?请你在图 2 中利用直尺和圆规找到符合题意的圆心 O，并写出你的作图方法．

27. 如图，已知二次函数 y=ax2−4ax+c 的图象交 x 轴于 A，B 两点（其中 A 点在 B 点的左侧），交 y 轴于点 C0,3．
（1）若 tan∠ACO=23，求这个二次函数的表达式；
（2）若 OC 为 OA，OB 的比例中项．
①设这个二次函数的顶点为 P，求 △PBC 的面积；
②若 M 为 y 轴上一点，N 为平面内一点，问：是否存在这样的 M，N，使得以 M，N，B，C 为顶点的四边形为矩形?若存在，请直接写出所有符合条件的点 N 的坐标：若不存在，请说明理由．

28. 如图，在菱形 ABCD 中，已知 ∠BAD=120∘，对角线 BD 长为 12．
（1）求菱形 ABCD 的周长．
（2）动点 P 从点 A 出发，沿 A→B 的方向，以每秒 1 个单位的速度向点 B 运动；在点 P 出发的同时，动点 Q 从点 D 出发，沿 D→C→B 的方向，以每秒 2 个单位的速度向点 B 运动．设运动时间为 ts．
①当 PQ 恰好被 BD 平分时，试求 t 的值；
②连接 AQ，试求：在整个运动过程中，当 t 取怎样的值时，△APQ 恰好是一个直角三角形?
答案
第一部分
1. B【解析】16 表示 16 的算术平方根．
2. C【解析】A、字母不同不是同类项，故A不符合题意；
B、相同字母的指数不同不是同类项，故B不符合题意；
C、 3x2y 的同类项的是 x2y；
D、相同字母的指数不同不是同类项，故D不符合题意．
3. D【解析】758 万平方米，这个数据用科学记数法可表示为 7.58×106 m2．
4. A【解析】∵m>n，
∴m−2>n−2，m−5>n−5，−2m<−2n，4m>4n．
5. D
【解析】A．对全国中学生心理健康现状的调查适宜于抽样调查，故A错误；
B．对冷饮市场上冰淇淋质量情况的调查适宜于抽样调查，故B错误；
C．对西安市市民实施低碳生活情况的调查，适宜于抽样调查，故C错误；
D．对“神舟九号”飞船零部件状况的检查要求精确度高，故D适宜于普查．
6. A【解析】根据主视图和左视图都为三角形，俯视图是矩形，可得这个几何体为四棱锥．
7. C【解析】①对顶角相等，是真命题；
②两直线平行，同位角相等，是假命题；
③在同圆中，同一条弧所对的圆周角相等，但同一条弦所对的圆周角不一定相等，是假命题；
④圆的内接四边形对角互补，是真命题．
8. A【解析】∵ 将边长为 3 cm 的正方形 ABCD 沿射线 AD 方向向右平移 2 cm 得到矩形 AʹBʹCD，
∴AʹBʹ=AB=3，AʹD=3−2=1，
∴ 平移前后图形的重叠部分的面积 =3×1=3 cm2．
9. B【解析】连接 OA，
∵C 为 AB 的中点，
∴AC=BC，
∴OC⊥AB，
∴AM=12AB=8，
设 OM=3a，则 CM=2a，
∴OC=5a，
由勾股定理得，OA2=AM2+OM2，即 5a2=82+3a2，
解得，a=2（负值舍去），
则 CM=2a=4cm．
10. B
【解析】∵OCAD 和 CEBG 都是正方形，
∴ 设 BE=a，AD=b，
∴Ba+b,a，Ab,b，
∵A，B 两点都在反比例函数 y=kx，
∴aa+b=b⋅b，
∴ba=1+52，
①四边形 ADFG 中宽与长的比为 b−ab，
将 ba=1+52 代入，得到 b−ab=3−52，
∴ 四边形 ADFG 不是黄金矩形；①不正确；
四边形 OCGF 中宽与长的比为 ab=5−12，
∴ 四边形 OCGF 为黄金矩形，②正确；
∵FG，OC 的中点分别为 P，Q，
∴OQ=12b，
四边形 OQPF 中宽与长的比为 12ba=1+54，
∴ 四边形 OQPF 不是黄金矩形；③不正确；
故选：B．
第二部分
11. 3
【解析】−−3=3，故 −3 的相反数是 3．
12. 2
【解析】当 x=3 时，原式=9a−9−4=5，解得：a=2．
13. xx−8x+8
【解析】x3−64x=xx2−82=xx−8x+8.
14. x≥2
【解析】2x−4≥0，解得 x≥2．
15. ③
【解析】①线段，②等腰三角形，③平行四边形，④圆．其中，不一定是轴对称图形的是③．
16. 126∘
【解析】∵a∥b，
∴∠1=∠3=54∘，
∴∠2=180∘−∠3=126∘．
17. 43+3
【解析】如图，将 △BPC 绕点 B 逆时针旋转 60∘ 得到 △BKA，
则 PB=BK=4，AK=PC=5，∠PBK=60∘，
∴△KBP 为等边三角形，
∴∠KPB=60∘，KP=4，
∵AP=3，
∴AP2+KP2=AK2，
∴∠APK=90∘，
∴∠APB=150∘，
作 BH⊥AP 于 H，则 ∠BPH=30∘，
∴BH=12BP=2，
∴△PBC 的面积=△AKB 的面积=S△APK+S△BPK−S△APB=12×3×4+34×42−12×2×3=3+43.
18. 223
【解析】当点 A，D，E 在同一条直线上时，AE 取得最大值．
过点 A 作 AM⊥BC 于点 M，
∵∠BAC=90∘，AB=AC=6，
∴BC=62+62=62，
∴BM=CM=32，
∵BD:DC=1:2，DE=BC，
∴BD=22，DE=EF=DG=FG=62，
∴DM=32−22=2，
在 Rt△ADM 中，AD=322+22=25，
在 Rt△ADG 中，AG=AD2+DG2=223．
第三部分
19. （1） 原式 =−22+4⋅32−23=4+23−23=4；
（2） 原式 =xx+1−x+2x−1x+1x−1=x2+x−x2+x−2x+1x−1=2x2−1．
20. （1）
2x+3x−3>6.5x>9.∴x>95.
（2）
2x−y=5, ⋯⋯①3x+2y=4. ⋯⋯②①×2+②
得：
7x=14.
解得：
x=2.
把 x=2 代入 ①，得
y=−1.∴
原方程组的解为
x=2,y=−1.
21. （1） 因为 △ACB 和 △ECD 都是等腰直角三角形，
所以 AC=BC，EC=DC．
因为 ∠ACE=∠DCE−∠DCA，∠BCD=∠ACB−∠DCA，∠ACB=∠ECD=90∘，
所以 ∠ACE=∠BCD．
在 △ACE 和 △BCD 中，
AC=BC,∠ACE=∠BCD,EC=DC,
所以 △ACE≌△BCDSAS．
（2） 又 ∠BAC=45∘，
由（1）可知 ∠EAC+∠B=45∘，AE=BD=12，
所以 ∠EAD=∠EAC+∠BAC=90∘，
即 △EAD 是直角三角形，
所以 DE=AE2+AD2=122+52=13．
22. （1） 30
【解析】2 个班参加体育类社团活动人数为 6÷20%=30（人）．
（2） 表示“棒球”项目的人数为：30−10−10−6=4（人），
如图所示：
（3） 600×4100=24（人）．
答：该校八年级共有 24 名学生参加“棒球”项目．
23. 分别记杨老师（女）、王老师（男），陈老师（女）、周老师（男）、王老师（女）为 A，B，C，D，E，
画树状图，得
∵ 共有 20 种等可能的结果，其中符合题意的情况有 6 种，
∴P（所抽取的 2 名评委恰好是都是女教师）=620=310．
24. （1） ∵M 为 OA 的中点，
∴ 可设 AM=OM=x．
∵ 四边形 OABC 是矩形，
∴BC=AO=2x．
由 △BCP 沿 PB 折叠，得 BQ=BC=2x，则 BM=BQ−MQ=2x−1．
在 Rt△ABM 中，由勾股定理得 x2+42=2x−12，
解得 x=3，
∴A−6,0．
（2） 如图，设 PQ 与 OA 相交于点 N．
在 △MQN 与 △MAB 中，
∠Q=∠A=90∘,∠NMQ=∠BMA.
∴△MQN∽△MAB，
∴MNMB=MQMA=QNAB，即 MN5=13=QN4，
∴MN=53，QN=43．
∴ON=OM−MN=3−53=43．
在 △MQN 与 △PON 中，
∠Q=∠PON=90∘,∠MNQ=∠PNO.
∴△MQN∽△PON，
∴OPQM=ONQN，即 OP1=4343，
∴OP=1，
∴P0,1．
设折痕 PB 所对应的函数表达式为 y=kx+b，
∵B−6,4，P0,1，
∴−6k+b=4,b=1.
解得 k=−12,b=1.
∴ 折痕 PB 所对应的函数表达式为 y=−12x+1．
25. （1） 4200
【解析】若采用租车位的方式，则每年共需缴费 300+50×12=4200（元）．
（2） 设每个车位的销售单价为 x 元，
若 6%⋅x−3600=3600，求得 x=63600，此时两种方案任选；
若 6%⋅x−3600>3600，求得 x>63600，
此时选用“租车位”方案合算；
若 6%⋅x−3600<3600，求得 x<63600，
此时选用“买车位”方案合算．
26. （1） △ACD 与 △ADE 相似，如图（1）所示，连接 OD，
∵⊙O 恰好与 BC 相切于点 D，
∴∠ODB=90∘，
又 ∵∠C=90∘，
∴OD∥AC，
∴∠ODA=∠DAC，
∵OD=OA，
∴∠ODA=∠OAD，
∴∠OAD=∠DAC，
∵AE 为 ⊙O 的直径，
∴∠ADE=90∘，
∴∠ADE=∠C，
∴△ACD∽△ADE．
（2） ∵△ACD∽△ADE，
∴3AD=AD4，
∴AD=23，
∵AC=3，
根据勾股定理得 CD=3，
∴sin∠DAC=12，
∴∠DAC=∠EAD=∠ODA=30∘，
∴∠AOD=120∘，
∴S△OAD=34OA2=3，
∴S=120∘⋅π⋅4360∘−3=4π3−3．
（3） 如图 2 所示，作图方法：
①以 A 为圆心，AC 长为半径画弧，交 AB 于点 H，以 H，C 为圆心，大于 12CH 长为半径画弧，交于点 G，连接 AG，AG 即为 ∠BAC 的角平分线，AG 与 BC 的交点即为点 D．
②以 D 为圆心，DC 长为半径画弧，交 BC 于点 Cʹ，以 C，Cʹ 为圆心，大于 12CCʹ 为半径画弧，分别交于点 E，F，连接 EF，EF 即为 CCʹ 的垂直平分线，EF 与 AB 的交点即为点 O．
27. （1） 在 Rt△AOC 中，C0,3，tan∠ACO=23，
∴A−2,0，
则有 c=3,4a+8a+c=0,
解得 a=−14,c=3,
∴ 二次函数的表达式为 y=−14x2+x+3．
（2） ① ∵ 对称轴 x=−−4a2a=2，如图 1 所示，
由 OC 为 OA，OB 的比例中项可得 △AOC∽△COB，
设点 A 的坐标为 m,0，则点 B 的坐标为 4−m,0，
则 OA=−m，OB=4−m，
∴−m3=34−m，
解得 m1=2+13（舍），m2=2−13，
∴A2−13,0，B13+2，
则有 c=3,a2−132−4a2−13+c=0,
解得 a=−13,c=3,
∴ 二次函数的解析式为 y=−13x2+43x+3，
∴P2,133，
设直线 BC 的解析式为 y=kx+b，
则有 b=3,2+13k+b=0,
解得 k=2−133,b=3,
∴ 直线 BC 的解析式为 y=2−133x+3，
过点 P 作 y 轴的平行线交 BC 于点 Q，
则 Q2,13−2133，
∴PQ=2133，
∴S=2133×12×2+13=133+2313．
②点 N 的坐标为 13+2,3 或 −13−2,−83−4313．
【解析】②存在，分两种情况．
情况一：如图 2 所示，
此时 M 于 O 重合，
∴N13+2,3．
情况二：如图 3 所示，
∵ 四边形 CBMN 为矩形，
∴∠CBM=90∘，
∴∠CBO=∠OMB，
∵∠COB=∠BOM，
∴△COB∽△BOM，
∴COBO=BOOM，即 32+13=2+13OM，
解得 OM=17+4133．
∴M0,−17+4133，
线段 NC 可以从 BM 平移得到，
点 B 与点 C 为对应点，点 M 与点 N 为对应点，
点 B 向左移动 2+13,0 个单位，向上移动 3 个单位得到点 C，
∴ 点 M 到点 N 也是同样得平移规律，
∴N−2−13,−83−4133．
综上，点 N 的坐标为 13+2,3 或 −13−2,−83−4313．
28. （1） 连接 AC 交 BD 于 O，如图 1 所示：
∵ 四边形 ABCD 是菱形，
∴AB=BC=CD=AD，AC⊥BD，∠BCD=∠BAD=120∘，∠BCO=12∠BCD=60∘，OB=OD=12BD=6，
在 Rt△BOC 中，BC=6sin60∘=632=43，
∴ 菱形 ABCD 的周长 =4×43=163．
（2） ①当点 Q 在 CD 边上时，
设 PQ 交 BD 于 M，则 PM=QM，
∵AB∥CD，
∴BPDQ=PMQM=1，
∴BP=DQ，
根据题意得：AP=t，DQ=2t，则 BP=43−t，
∴43−t=2t，
解得：t=433；
当点 Q 在 CB 边上时，不存在．
②当点 Q 在 CD 边上时，若 ∠PAQ=90∘，如图 2 所示：
∵AB∥CD，
∴∠AQD=∠PAQ=90∘，
∴∠DAQ=30∘，
∴DQ=12AD=23，
即 2t=23，
解得：t=3；
若 ∠APQ=90∘，如图 3 所示：
作 AN⊥CD 于 N，则 ∠PAN=90∘，NQ=AP=t，
∴∠DAN=30∘，
∴DN=12AD=23，
∵DQ=DN+NQ，
∴2t=23+t，
解得：t=23；
当点 Q 在 CB 边上时，如图 4 所示：
根据题意得：AP=t，BP=43−t，CQ=2t−43，
∴BQ=43−2t−43=83−2t，
∴BP=12BQ，
作 QH⊥BP 于 H，
∵∠ABC=60∘，
∴∠BQH=30∘，
∴BH=12BQ=43−t，
∴BP=BH，即 H 与 P 重合，
∴∠BPQ=90∘，
即 ∠APQ=90∘ 恒成立．
∴ 当 23≤t<43 时 △APQ 都为直角三角形．
综上可得，当 t=3 或 23≤t<43 时，△APQ 恰好为直角三角形．