八年级上册第2章 特殊三角形2.5 逆命题和逆定理说课课件ppt

这是一份八年级上册第2章 特殊三角形2.5 逆命题和逆定理说课课件ppt，文件包含课件25逆命题和逆定理初中完全同步系列浙教版数学八年级上册ppt、习题25逆命题和逆定理-浙教数学八上docx等2份课件配套教学资源，其中PPT共11页， 欢迎下载使用。

下列句子是命题的是（ ） A.画∠AOB=45° B. 小于直角的角是锐角吗？ C.连结CD D. 会飞的交通工具是飞机
判断某一件事情的句子叫做命题.
命题由条件和结论两部分构成.
正确的命题叫做真命题；不正确的命题叫做假命题.
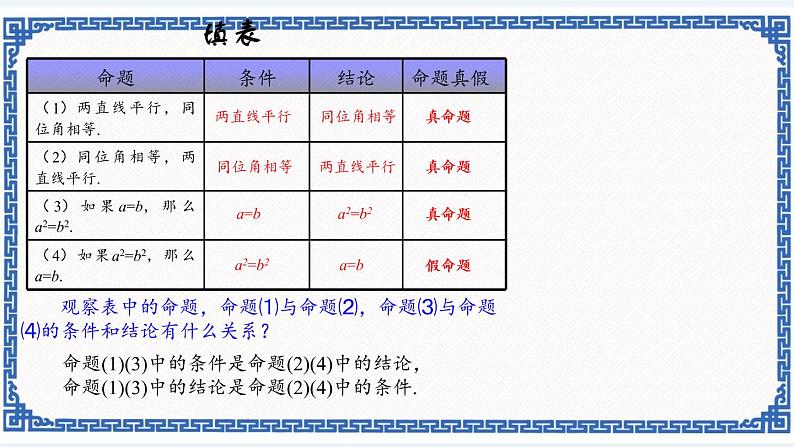
　　观察表中的命题，命题⑴与命题⑵，命题⑶与命题⑷的条件和结论有什么关系？
命题(1)(3)中的条件是命题(2)(4)中的结论，命题(1)(3)中的结论是命题(2)(4)中的条件.
在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.
　　我们把其中一个命题叫做原命题，另一个命题叫做它的逆命题.
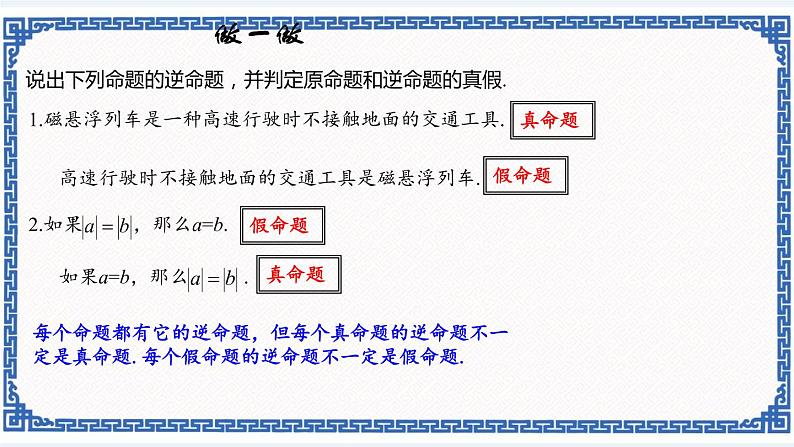
说出下列命题的逆命题，并判定原命题和逆命题的真假.
1.磁悬浮列车是一种高速行驶时不接触地面的交通工具.
高速行驶时不接触地面的交通工具是磁悬浮列车.
每个命题都有它的逆命题，但每个真命题的逆命题不一定是真命题.每个假命题的逆命题不一定是假命题.
如果一个定理的逆命题能被证明是真命题，那么就叫它是原定理的逆定理，这两个定理叫做互逆定理.
下列定理中，哪些有逆定理？如果有逆定理，请说出逆定理.
（1）同旁内角互补，两直线平行.
两直线平行，同旁内角互补.
下列说法哪些正确，哪些不正确？
（4）每个定理都有逆定理.
（1）每个命题都有逆命题.
（2）假命题没有逆命题.
（3）真命题的逆命题是真命题.
（5）逆定理有真有假.
说出定理“线段垂直平分线上的点到线段两端的距离相等”的逆命题，并证明这个逆命题是真命题.
解:这个定理的逆命题是:到线段两端距离相等的点在线段的垂直平分线上．
已知:如图,AB是一条线段,P是一点,且PA=PB.求证：点P在线段AB的垂直平分线上.
（1）当点P不在线段AB上时；
（2）当点P在线段AB上时.
说出命题“两个全等三角形的面积相等”的逆命题，判断这个逆命题的真假，并给出证明.
解:逆命题是“如果两个三角形的面积相等，那么这两个三角形全等.”
写出定理“等腰三角形底边上的高线与中线互相重合”的逆命题，并证明这个逆命题是真命题.
解:这个定理的逆命题是:底边上的高线与中线互相重合的三角形是等腰三角形．
已知:如图,在△ABC中，AD⊥BC，且AD平分BC.求证：△ABC为等腰三角形.