2020-2021学年天津市西青区八上期末数学试卷

这是一份2020-2021学年天津市西青区八上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列等式从左到右的变形，是因式分解的是
A. 2xx+3=2x2+6xB. 24xy2=3x⋅8y2
C. x2+2xy+y2+1=x+y2+1D. x2−y2=x+yx−y

2. 下列计算结果正确的是
A. a3÷a=a2B. a23=a5
C. a2⋅a3=a6D. −3a2b2=6a4b2

3. 分式 x−1x+2 的值为 0，则 x 的值是
A. −2B. −1C. 0D. 1

4. 已知某新型感冒病毒的直径约为 0.000000823 米，将 0.000000823 用科学记数法表示为
A. 8.23×10−6B. 8.23×10−7C. 8.23×106D. 8.23×107

5. 如果一个多边形的每个外角都等于 36∘，那么这个多边形是
A. 六边形B. 八边形C. 十边形D. 十二边形

6. 下列图形中，不是轴对称图形的是
A. B.
C. D.

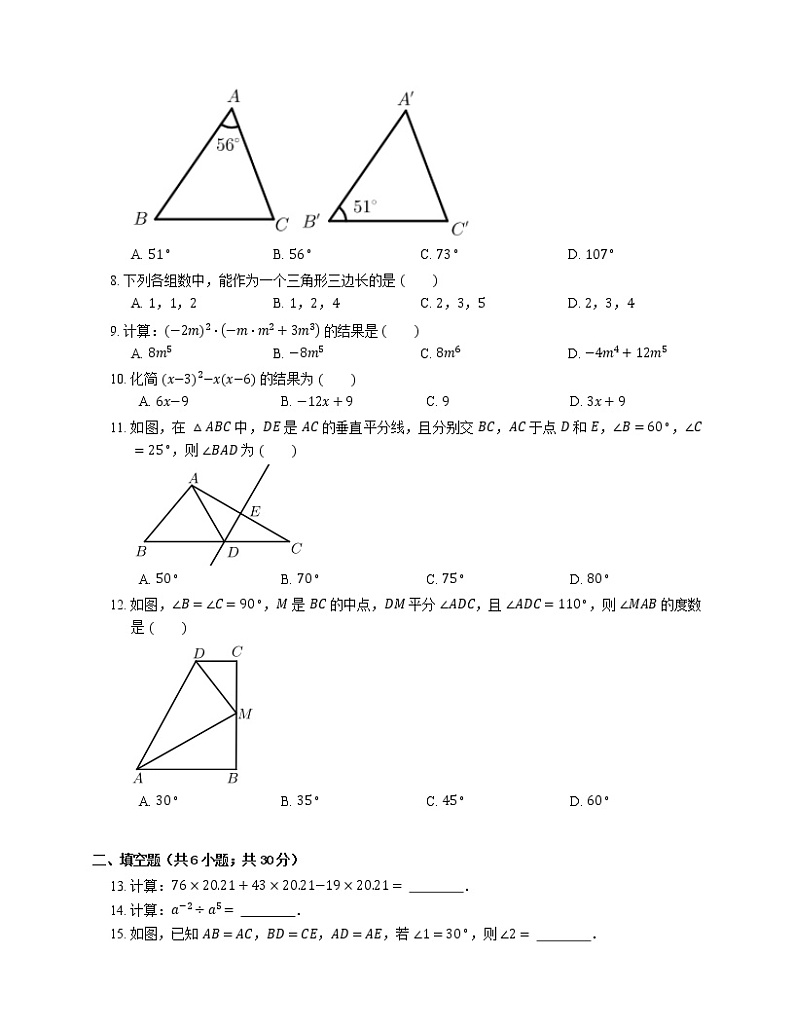
7. 如图，△ABC≌△AʹBʹCʹ，则 ∠C 的度数是
A. 51∘B. 56∘C. 73∘D. 107∘

8. 下列各组数中，能作为一个三角形三边长的是
A. 1，1，2B. 1，2，4C. 2，3，5D. 2，3，4

9. 计算：−2m2⋅−m⋅m2+3m3 的结果是
A. 8m5B. −8m5C. 8m6D. −4m4+12m5

10. 化简 x−32−xx−6 的结果为
A. 6x−9B. −12x+9C. 9D. 3x+9

11. 如图，在 △ABC 中，DE 是 AC 的垂直平分线，且分别交 BC，AC 于点 D 和 E，∠B=60∘，∠C=25∘，则 ∠BAD 为
A. 50∘B. 70∘C. 75∘D. 80∘

12. 如图，∠B=∠C=90∘，M 是 BC 的中点，DM 平分 ∠ADC，且 ∠ADC=110∘，则 ∠MAB 的度数是
A. 30∘B. 35∘C. 45∘D. 60∘

二、填空题（共6小题；共30分）
13. 计算：76×20.21+43×20.21−19×20.21= ．

14. 计算：a−2÷a5= ．

15. 如图，已知 AB=AC，BD=CE，AD=AE，若 ∠1=30∘，则 ∠2= ．

16. 若 2x=5，则 2y=3，则 22x+y 的值为 ．

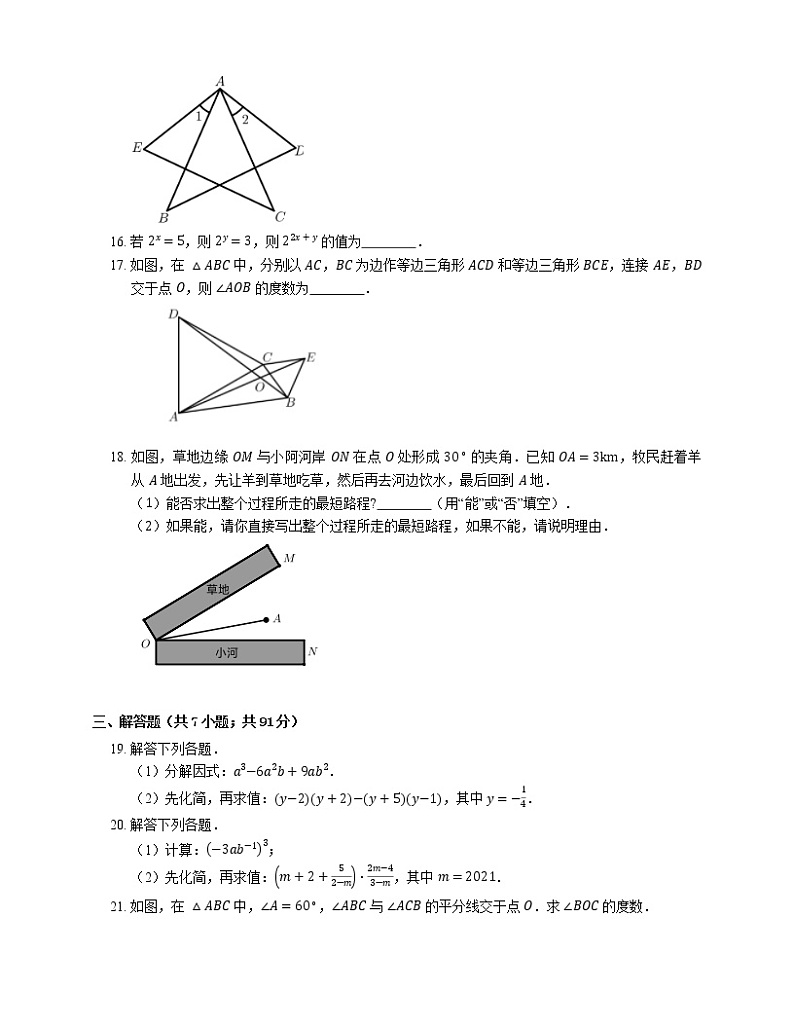
17. 如图，在 △ABC 中，分别以 AC，BC 为边作等边三角形 ACD 和等边三角形 BCE，连接 AE，BD 交于点 O，则 ∠AOB 的度数为 ．

18. 如图，草地边缘 OM 与小阿河岸 ON 在点 O 处形成 30∘ 的夹角．已知 OA=3km，牧民赶着羊从 A 地出发，先让羊到草地吃草，然后再去河边饮水，最后回到 A 地．
（1）能否求出整个过程所走的最短路程? （用“能”或“否”填空）．
（2）如果能，请你直接写出整个过程所走的最短路程，如果不能，请说明理由．

三、解答题（共7小题；共91分）
19. 解答下列各题．
（1）分解因式：a3−6a2b+9ab2．
（2）先化简，再求值：y−2y+2−y+5y−1，其中 y=−14．

20. 解答下列各题．
（1）计算：−3ab−13；
（2）先化简，再求值：m+2+52−m⋅2m−43−m，其中 m=2021．

21. 如图，在 △ABC 中，∠A=60∘，∠ABC 与 ∠ACB 的平分线交于点 O．求 ∠BOC 的度数．

22. 如图，△ABC 在平面直角坐标系中，点 A，B，C 的坐标分别为 A4,4，B1,2，C3,1．
（1）请在平面直角坐标系内，画出 △ABC 关于 y 轴对称的图形 △A1B1C1，其中，点 A，B，C 的对应点分别为 A1，B1，C1．
（2）请写出点 C3,1 关于直线 n（直线 n 上各点的纵坐标都为 −2）对称的点 C2 的坐标 ．

23. 注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路，填写表格．并完成本题解答的全过程．如果你选用其他的解题方案，此时，不必填写表格，只需按照解答题的一般要求，进行解答即可．甲、乙二人做某种机械零件．已知甲每小时比乙多做 6 个，甲做 90 个所用的时间与乙做 60 个所用的时间相等．求甲、乙每小时各做零件多少个．
设乙每小时做零件 x 个．
（1）根据题意，用含有 x 的式子填写下表：
工作量个工作效率个/h工作时间h甲90乙60x
（2）列出方程，求出问题的解并写出答话．

24. 在 △ABC 中，AB=AC，D 为 BC 边中点，DE⊥AB，DF⊥AC，垂足分别为 E，F．
（1）如图，求证：DE=DF．
（2）若 ∠B=60∘，BE=2，求 △ABC 的周长．

25. 在 △ABC 中，AB=AC，过点 B 作 PB⊥BC，垂足为 B，∠BPC=∠BAC，PC 与 AB 交于点 E．
（1）如图，∠ABC=60∘，PC=4，求 PB 的长．
（2）如图，∠BAC=60∘，D 为 PC 边上的一点，PD=PB，求证：PA+PB=PC．
（3）如图，AM⊥PC，AN⊥BN，垂足分别为 M，N，BN=5，求 PB+PC 的长．
答案
第一部分
1. D【解析】A选项：等号左侧是单项式与多项式乘积的形式，故A错误；
B选项：等号左侧是一个单式，故B错误；
C选项：等号右侧不是整式乘积的开式，故C错误；
D选项：只有选项D从左到右的变形才是因式分解，故D正确．
2. A【解析】A选项：a3÷a=a2，故A选项正确；
B选项：a23=a6，故B选项错误；
C选项：a2⋅a3=a5，故C选项错误；
D选项：−3a2b2=9a4b2，故D选项错误．
3. D【解析】当 x−1x+2=0 时，x=1．
4. B
5. C
【解析】∵ 一个多边形的每个外角都等于 36∘，
∴ 多边形的边数为 360∘÷36∘=10．
6. B【解析】一个图形沿着某条直线翻折，直线两旁的部分能够完全重合，这个图形叫做轴对称图形，这条直线是它的对称轴．
A选项：根据轴对称图形的定义，是轴对称图形，故A错误；
B选项：根据轴对称图形的定义，不是轴对称图，故B正确；
C选项：不符合轴对称图形的定义，是轴对称图形，故C错误；
D选项：根据轴对称图形的定义，是轴对称图形．故D错误．
7. C【解析】因为 △ABC≌△AʹBʹCʹ，
所以 ∠A=∠Aʹ=56∘，∠B=∠Bʹ=51∘，
所以 ∠C=180∘−∠A−∠B=180∘−56∘−51∘=73∘．
8. D【解析】A选项：1+1=2，故不能作为三角形三边长；
B选项：1+2=3<4，故不能作为三角形三边长；
C选项：2+3=5，故不能作为三角形三边长；
D选项：2+3=5>4，故能作为三角形三边长．
9. A【解析】原式=−22m2⋅−m3+3m3=4m2⋅2m3=8m5.
10. C
【解析】原式=x2−6x+9−x2+6x=9．
11. B【解析】方法一：
∵DE 是 AC 的垂直平分线，
∴DA=DC，
∴∠DAC=∠C=25∘，
∵∠B=60∘，∠C=25∘，
∴∠BAC=95∘，
∴∠BAD=∠BAC−∠DAC=70∘．
方法二：
∵DE 是 AC 的垂直平分线，
∴AD=DC，
∴∠DAC=∠C=25∘，
∵∠B+∠C+∠BAD+∠DAC=180∘，
∴∠BAD=180∘−60∘−25∘−25∘=70∘．
12. B【解析】作 MN⊥AD 于 N．
∵∠B=∠C=90∘，
∴AB∥CD，
∴∠DAB=180∘−∠ADC=70∘，
∵DM 平分 ∠ADC，MN⊥AD，MC⊥CD，
∴MN=MC，
∵M 是 BC 的中点，
∴MC=MB，
∴MN=MB，又 MN⊥AD，MB⊥AB，
∴∠MAB=12∠DAB=35∘．
第二部分
13. 2021
【解析】76×20.21+43×20.21−19×20.21=76+43−19×20.21=100×20.21=2021.
14. 1a7
【解析】a−2÷a5=a−2−5=a−7=1a7．
15. 30∘
【解析】在 △ABD 和 △ACE 中，
AB=AC,AD=AE,BD=CE,
△ABD≌△ACESSS，
∴∠BAD=∠CAE，
∴∠BAD−∠BAC=∠CAE−∠BAC，
即 ∠1=∠2，
∵∠1=30∘，
∴∠2=30∘．
16. 75
【解析】∵2x=5，2y=3，
∴22x+y=2x2⋅2y=52⋅3=75.
17. 120∘
【解析】如图：AC 与 BD 交于点 H．
∵△ACD，△BCE 都是等边三角形，
∴CD=CA，CB=CE，
∠ACD=∠BCE=60∘，
∴∠DCB=∠ACE，
在 △DCB 和 △ACE 中，
CD=CA,∠DCB=∠ACE,CB=CE,
∴△DCB≌△ACE，
∴∠CAE=∠CDB，
∵∠DCH+∠CHD+∠BDC=180∘，
∠AOH+∠AHO+∠CAE=180∘，
∠DHC=∠OHA，
∴∠AOH=∠DCH=60∘，
∴∠AOB=180∘−∠AOH=120∘．
18. 能，3km
【解析】（1）能求出整个过程所走的最短路程．
（2）分别画出点 A 关于 OM，ON 的对称点 B，C，连接 BC 交 OM，ON 于点 D，E，连接 AD，AE，则线段 AD，DE，EA 即为所示路径，
根据对称的性质：OB=OA=OC=3，
∠BOC=∠BOA+∠AOC=2∠MON=60∘，
∴△BCO 为等边三角形，
∴BC=3，故其总路程为 3km．
第三部分
19. （1） a3−6a2b+9ab2=aa2−6ab+9b2=aa−3b2.
（2） 原式=y2−4−y2+4y−5=y2−4−y2−4y+5=−4y+1,
当 y=−14 时，
原式=−4×−14+1=1+1=2.
20. （1） 原式=−3ab3=−27a3b3.
（2） 原式=2+m2−m2−m+52−m×2m−23−m=4−m2+52−m×−22−m3−m=3+m3−m2−m×−22−m3−m=−23+m=−6−2m.
当 m=2021 时，
原式=−6−2×2021=−6−4042=−4048.
21. ∵∠A=60∘，
∴∠ABC+∠ACB=180∘−∠A=120∘，
∵OB 平分 ∠ABC，OC 平分 ∠ACB，
∴∠OBC=12∠ABC，∠OCB=12∠ACB，
∴∠OBC+∠OCB=12∠ABC+∠ACB=60∘，
∴∠BOC=180∘−∠OBC+∠OCB=120∘．
22. （1） 如图 1 所示：△A1B1C1 即为所求．
（2） 3,−5
【解析】如图 2 所示：C2 即为所求，
由图 2 可知：C23,−5．
23. （1） ∵ 乙每小时做 x 个，甲每小时比乙多做 6 个，
∴ 甲每小时做 x+6 个，
∵ 甲工作量为 90 个，乙工作量为 60 个，
∴ 甲工作时间为：90x+6h，乙工作时间为：60xh，
∴ 表格为：
工作量个工作效率个/h工作时间h甲90x+690x+6乙60x60x
（2） ∵ 甲做 90 个所用时间与乙做 60 个所用时间相等，
∴90x+6=60x，
∴x=120，经检验，符合题意，
∴x+6=126，
∴ 甲每小时做 126 个，乙每小时做 120 个．
24. （1） ∵DE⊥AB，DF⊥AC，
∴∠BED=∠CFD=90∘，
∵AB=AC，
∴∠B=∠C（等边对等角）．
∵D 是 BC 的中点，
∴BD=CD．
在 △BED 和 △CFD 中，
∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFDAAS，
∴DE=DF．
（2） ∵AB=AC，∠A=60∘，
∴△ABC 为等边三角形，
∴∠B=60∘，
∵∠BED=90∘，
∴∠BDE=30∘，
∴BE=12BD，
∵BE=1，
∴BD=2，
∴BC=2BD=4，
∴△ABC 的周长为 12．
25. （1） ∵AB=AC，∠ABC=60∘，
∴△ABC 是等边三角形，
∴∠BAC=60∘，
∴∠BPC=∠BAC=60∘，
∵PB⊥BC，
∴∠PBC=90∘，
∴∠PCB=30∘，
∴PB=12PC=12×4=2．
（2） ∵AB=AC，∠BAC=60∘，
∴△ABC 是等边三角形，
∴BA=BC，∠ABC=60∘，
∵∠BPC=∠BAC=60∘，PB=PD，
∴△PBD 是等边三角形，
∴∠PBD=60∘，PB=PD=BD，
∴∠ABC=∠PBD，
∴∠ABC−∠ABD=∠PBD−∠ABD，即 ∠DBC=∠PBA，
在 △DBC 和 △PBA 中
BD=BP,∠DBC=∠PBA,BC=BA,
∴△DBC≌△PBA，
∴DC=PA，
∵PD+DC=PC，
∴PA+PB=PC．
（3） ∵AM⊥PC，AN⊥BN，
∴∠CMA=∠BNA=90∘=∠AMP，
∵∠BPC=∠BAC，∠PEB=∠AEC，
∴∠ABN=∠ACM，
在 △CMA 和 △BNA 中
∠CMA=∠BNA,∠ACM=∠ABN,AC=AB,
∴△CMA≌△BNAAAS，
∴AM=AN，CM=BN=5，
在 Rt△AMP 和 Rt△ANP 中
AM=AN,AP=AP,
∴Rt△AMP≌Rt△ANPHL，
∴MP=NP，
∴MP+PB=NP+PB=BN=5，
∴PB+PC=PB+PM+CM=5+5=10．