2020-2021学年广东省深圳市福田区深圳市高级中学七上期末数学试卷

这是一份2020-2021学年广东省深圳市福田区深圳市高级中学七上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 在有理数 1，−12，−1，0 中，最小的数是
A. 1B. −12C. −1D. 0

2. 2019 新型冠状病毒的直径是 0.00012 mm，将 0.00012 用科学记数法表示是
A. 120×10−6B. 12×10−3C. 1.2×10−4D. 1.2×10−5

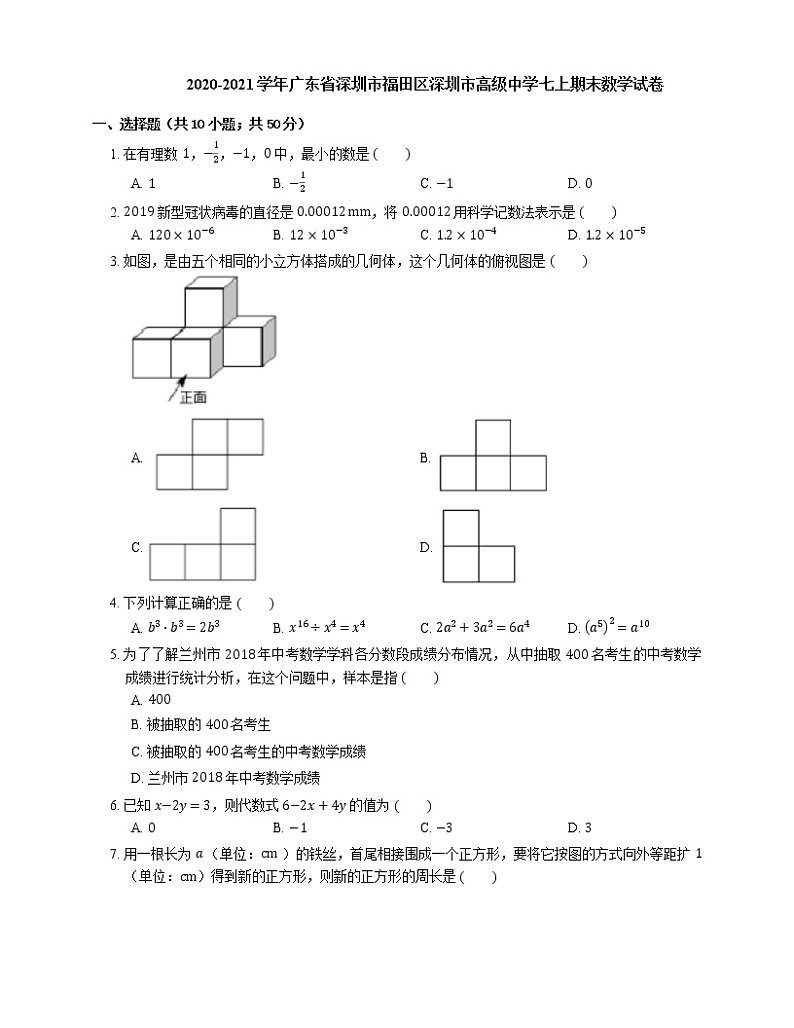
3. 如图，是由五个相同的小立方体搭成的几何体，这个几何体的俯视图是
A. B.
C. D.

4. 下列计算正确的是
A. b3⋅b3=2b3B. x16÷x4=x4C. 2a2+3a2=6a4D. a52=a10

5. 为了了解兰州市 2018 年中考数学学科各分数段成绩分布情况，从中抽取 400 名考生的中考数学成绩进行统计分析，在这个问题中，样本是指
A. 400
B. 被抽取的 400 名考生
C. 被抽取的 400 名考生的中考数学成绩
D. 兰州市 2018 年中考数学成绩

6. 已知 x−2y=3，则代数式 6−2x+4y 的值为
A. 0B. −1C. −3D. 3

7. 用一根长为 a （单位：cm ）的铁丝，首尾相接围成一个正方形，要将它按图的方式向外等距扩 1（单位：cm）得到新的正方形，则新的正方形的周长是
A. 4 cmB. 8 cmC. a+4 cmD. a+8 cm

8. 《孙子算经》中有一道题，原文是：今有三人共车，一车空：二人共车，九人步，问人与车各几何?译文为：今有若干人乘车，每 3 人共乘一车，最终剩余 2 辆车：若每 2 人共乘一车，最终剩余 9 个人无车可乘，问共有多少人，多少辆车?设共有 x 人，可列方程
A. x+23=x2−9B. x3+2=x−92C. x3−2=x+92D. x−23=x2+9

9. 下列正确的有 个．
①倒数等于本身的数是 0，1，−1．
②多项式与单项式的和一定是多项式．
③如果 ∠POB=12∠AOB，则 OP 是平分 ∠AOB．
④ −0.82021×−542020=0.8．
A. 3B. 2C. 1D. 0

10. 已知：m=a+bc+2b+ca+3c+ab，且 abc>0，a+b+c=0，m 最大值是 x，最小的值是 y，则 x+y=
A. −4B. 2C. −2D. −6

二、填空题（共5小题；共25分）
11. 若 xa−1y3 与 12x4y3 是同类项，则 a 的值是 ．

12. 某种商品每件的进价为 120 元，标价为 180 元．为了拓展销路，商店准备打折销售．若使利润率为 20%，则商店应打 折．

13. 已知 2x+5y−3=0，则 4x⋅32y= ．

14. 若线段 AB=10cm，在直线 AB 上有一点 C，且 BC=4cm，M 是线段 AC 的中点，则 BM= cm．

15. 已知：20=1，21=2，22=4，23=8，24 的个位数是 6，25 的个位数是 2，⋯，则 20+21+22+23+24+⋯+22021 的个位数字是 ．

三、解答题（共7小题；共91分）
16. 解答下列各题：
（1）计算：−32−20210+∣−2∣−13−2×−19．
（2）解方程：x6−1+x4=−1．

17. 先化简，再求值：2x2y+xy−3x2y−xy−4x2y，其中 x=1，y=−1．

18. 某校对七年级学生进行“综合素质”评价，评价的结果分为 A，B，C，D 四个等级，现从中随机抽查了若干名学生的“综合素质”等级作为样本进行数据处理，并绘制以下两幅不完整的统计图．根据统计图提供的信息，解答下列问题：
（1）B 等级人数所占百分比是 ；C 等级所在扇形的圆心角是 度．
（2）请补充完整条形统计图．
（3）若该校七年级学生共 1000 名，请根据以上调查结果估算：评价结果为 A 等级或 B 等级的学生共有 名．

19. 如图，已知 a，b，c 在数轴上的位置．
（1）a+b 0，abc 0，ac 0．（填“>”或“<”）
（2）如果 a，c 互为相反数，求 ac= ．
（3）化简：∣b+c∣−2∣a−b∣−∣b−c∣．

20. 甲、乙两家商场同时出售同样的暖瓶和水杯，根据图中信息，回答下列问题：
（1）求一个暖瓶与一个水杯售价分别是多少元．
（2）为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送二个水杯，单独买水杯不优惠．若必须买 5 个暖瓶，且购买水杯个数大于 10 个，则当买多少个水杯时到两家商场一样合算．

21. 已知 O 是 AB 上的一点，从 O 点引出射线 OC，OE，OD，其中 OE 平分 ∠BOC．
（1）如图 1，若 ∠COD 是直角，∠DOE=15∘，求 ∠AOC 的度数．
（2）如图 2，若 ∠BOD=60∘，∠AOC=3∠DOE，求 ∠AOC 的度数．
（3）将图 1 中的 ∠COD（∠COD 仍是直角）绕顶点 O 顺时针旋转至图 3 的位置，设 ∠AOE=α，∠DOE=β，请猜想 α 与 β 之间存在什么样的数量关系，并说明理由．

22. a 是多项式 x3+4x2y2−1 的常数项，b 是该多项式的次数，c 是最小的正整数．
（1）a= ，b= ，c= ．
（2）在数轴上，点 A，B，C 分别对应实数 a，b，c．
①数轴上点 P 到点 A 的距离是点 P 到点 B 的距离的 2 倍，求点 P 对应的数．
②动点 M 从点 A 出发以 3 个单位速度向右运动，动点 N 从点 B 出发以 1 个单位速度向右运动，点 D 在数轴上对应的数是 10，动点 M 与动点 N 同时出发，当 M 运动到 D 后立即以原来的速度向左运动，设运动时间是 t，直接写出 t 为何值时，M，N 两点到点 C 的距离相等．
答案
第一部分
1. C【解析】∵−1<−12<0<1，
∴ 最小的数是 −1．
2. C【解析】0.00012=1.2×10−4．
3. A【解析】观察图形可知，这个几何体的俯视图是．
4. D【解析】A选项：b3⋅b3=b6≠2b3，故A错误；
B选项：x16÷x4=x12≠x4，故B错误；
C选项：2a2+3a2=5a2≠6a4，故C错误；
D选项：a52=a10，故D正确．
5. C
【解析】样本是指从总体中取出一部分个体，叫做这个总体的样本．
6. A【解析】∵ x−2y=3，
∴ 2x−2y=2×3=6，
∴ 6−2x+4y=6−2x−2y=6−6=0.
7. D【解析】设原正方形边长为 m 厘米，
则现正方形边长为 m+2 厘米，
由题可得：4m=a，
m=a4，
故现正方形周长为：
4m+2=4a4+2=a+8 cm，
故选D．
8. B【解析】设有 x 人，根据车的辆数不变列出等量关系，
每 3 人共乘一车，最终剩余 2 辆车，则车辆数为：x3+2，
每 2 人共乘一车，最终则余 9 个人无车可乘，则车辆数为：x−92
∴ 列出程为：x3+2=x−92．
9. D【解析】①倒数等于本身的数是 ±1，故①不正确；
②多项式与单项式的和不一定是多项式，也可能是单项式，例如：2a+2b+−2a=2b．故②不正确；
③如果 ∠POB=12∠AOB，则 OP 不一定平分 ∠AOB，例如：
故③不正确；
④
−0.82021×−542020=−0.82021×542020=−0.8×542020×0.8=−1×0.8=−0.8≠0.8
故④不正确，故正确的有 0 个．
10. A
【解析】∵abc>0，
∴a，b，c 为三正或两负一正，
∵a+b+c=0，
∴a，b，c 为两负一正，
a+bc=−cc=cc=±1，
b+ca=−aa=aa=±1，
c+ab=−bb=bb=±1，
∴mmax=x=−1+−2+3=0，
mmin=y=−3+−2+1=−4，
∴x+y=0+−4=−4．
第二部分
11. 5
【解析】因为 xa−1y3 与 12x4y3 是同类项，
所以 a−1=4，
所以 a=5．
12. 8
【解析】设商店打 x 折，
依题意，得：180×x10−120=120×20%，
解得：x=8．
13. 8
【解析】由已知得 2x+5y=3，
原式=22x⋅25y=22x+5y=23=8．
14. 3 或 7
【解析】①
BM=AB−AM=10−12AC=10−12AB+BC=10−12×10+4=10−12×14=10−7=3cm;
②
BM=MC+BC=12AC+BC=12AB−BC+BC=12×10−4+4=12×6+4=7cm.
15. 3
【解析】∵20=1，21=2，22=4，23=8，
24 的个位数是 6，
25 的个位数是 2，
∴ 每 4 个会循环一次，且个位和为 0，
∴20+21+22+23+24+⋯+22021 的个位数字：
1+0×20204+2=3．
第三部分
16. （1） 原式=−9−1+2−9×−19=−10+2+1=−7.
（2）
x6−1+x4=−1,2x−3−3x=−12,2x−3x=−12+3,−x=−9,x=9.
17. 2x2y+xy−3x2y−xy−4x2y=2x2y+2xy−3x2y+3xy−4x2y=−5x2y+5xy.
把 x=1，y=−1 代入，
原式=−5×12×−1+5×1×−1=0．
18. （1） 25%；72
【解析】4÷10%=40（人），
40−18−8−440×100%=25%，
840×360∘=72∘．
（2） 所作图形如下：
（3） 700
【解析】1000×40−8−440=700（名）．
19. （1） <；<；<
【解析】∵a<0，b>0，∣a∣>∣b∣，
∴a+b<0．
∵a<0，b>0，c>0，
∴abc<0．
∵a<0，c>0，
∴ac<0．
（2） −1
【解析】∵a，c 互为相反数，且不为 0，
∴ac=a−a=−1．
（3） ∣b+c∣−2∣a−b∣−∣b−c∣=b+c−2−a+b−−b+c=b+c+2a−2b+b−c=2a.
20. （1） 设一个暖瓶售价是 x 元，则一个水杯售价 34−x 元，
2x+334−x=70.34−x=2.x=32.
答：一个暖瓶与一个水杯售价分别是 32 元和 2 元
（2） 设买了 m 个水杯，
32×5+2m×0.9=5×32+2m−10.m=20.
答：当买 20 个水杯时到两家商场一样合算．
21. （1） 因为 ∠COD 是直角，
所以 ∠COD=90∘，
因为 ∠DOE=15∘，
所以
∠COE=∠COD−∠DOE=90∘−15∘=75∘.
因为 OE 平分 ∠BOC，
所以 ∠BOC=2∠COE=150∘，
所以 ∠AOC=180∘−∠BOC=30∘．
（2） 设 ∠DOE=α，则 ∠AOC=3∠DOE=3α，
因为 ∠BOD=60∘，
所以 ∠BOE=∠BOD+∠DOE=60∘+α，
因为 OC 平分 ∠BOC，
所以 ∠BOC=2∠BOE=120∘+2α，
因为 ∠AOC+∠BOC=180∘，
所以 3α+120∘+2α=180∘，
5α=60∘，
α=12∘．
所以 ∠AOC=36∘．
（3） α=2β；
因为 ∠COD 是直角，
所以 ∠COD=90∘，
因为 ∠DOE=β，
所以 ∠COE=∠COD−∠DOE=90∘−β，
因为 OE 平分 ∠BOC，
所以 ∠BOC=2∠COE=180∘−2β，
因为 ∠AOC+∠BOC=180∘，
所以 α+180∘−2β=180∘，
所以 α=2β．
22. （1） −1；4；1
【解析】∵ 多项式 x3+4x2y2−1 的常数项为 −1，次数为 4 次，
∴a=−1，b=4，
∵c 是最小的正整数，
∴c=1．
（2） ①设 P 点表示的数为 x，
∴PA=x+1，PB=x−4，
∵PA=2PB，
∴x+1=2x−4，
即 x+1=2x−4 或 x+1=24−x，
解得 x=9 或 x=73，
∴P 点对应的数为 9 或 73．
② 52 秒或 174 秒或 232 秒．
【解析】② ∵AC=10−−1=11，
∴ 当 M 运动到 D 点时，所花的时间为 113 秒，
当 0 M 点表示的数为 −1+3t，
N 点表示的数为 4+t，
当 M，N 重合时，M，N 到点 C 的距离相等，−1+3t=4+t，
解得 t=52，
当 t>113 时，
M 点表示的数为 10−3t−113=21−3t，
N 点表示的数为 4+t，
当 M，N 两点到 C 距离相等，则 C 点为 M，N 的中点或 M，N 第二次重合时，
∴21−3t+4+t=2×1 或 4+t=21−3t，
解得 t=232 或 t=174，
∴ 当 t=52秒或174秒或232秒 时，M，N 两点到点 C 的距离相等．