初中数学北师大版九年级上册1 反比例函数学案及答案

这是一份初中数学北师大版九年级上册1 反比例函数学案及答案，共8页。学案主要包含了如图5，已知一次函数的图象与轴等内容，欢迎下载使用。
教学内容
反比例函数的性质图像与应用二
教学目标
反比例函数的性质与应用类型的梳理与总结
重点
反比函数的求以及函数间的准确结合
难点
应用知识点准确解题
知识点的回顾：
反比例函数的定义、性质、反比例函数与一次函数的性质有哪些相同点与不同点：
反比例函数与一次函数的结合题型有哪些：
例题展现：
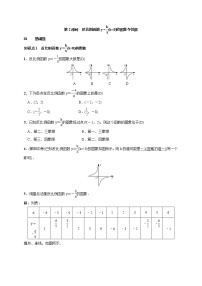
例一、1、反比例函数图象上有三个点，，，其中，
则，，的大小关系是( )

A． B． C． D．
2、如图，已知梯形ABCO的底边AO在轴上，BC∥AO，AB⊥AO，过点C的双曲线 交OB于D，且OD：DB=1:2，若△OBC的面积等于3，则k的值（ ）
A．等于2B．等于C．等于D．无法确定
3、函数的图象与直线没有交点，那么k的取值范围是（ ）
A． B． C． D．
4、已知反比例函数，下列结论不正确的是
A．图象必经过点(-1,2) B．y随x的增大而增大
C．图象在第二、四象限内 D．若x＞1，则y＞-2
5、已知函数是反比例函数，且图象在第二、四象限内，则m的值是（ ）
A．2 B．－2 C．±2 D．
6、如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB＝18，BC＝12，AC＝9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图像上的是（ ）
A．点G B．点EC．点DD．点F．
7、如图所示，点A是双曲线 y=（x＞0）上的一动点，过A作AC⊥y轴，垂足为点C，作AC的垂直平分线双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时，四边形ABCD的面积 D
A.逐渐变小 B.由大变小再由小变大 C.由小变大再有大变小 D.不变
8、在同一直角坐标系中，正比例函数的图象与反比例函数的图象有公共点，则 0
9、如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为2，则这个反比例函数的解析式为______________．
A
B
P
x
y
O
10、如图，一次函数与反比例函数的图象相交于A、B两点，若A点的坐标为（－2，3），则B点的坐标为____________。
y
1
x
O
A
B
C
图3
11、函数中，自变量的取值范围是 ．
12、如图3，Rt△ABC在第一象限，，AB=AC=2，
点A在直线上，其中点A的横坐标为1，且AB∥轴，
AC∥轴，若双曲线与△有交点，则k的
取值范围是 .
例二、在同一坐标系中，某反比例函数的图象与其正比例函数的图象相交于A、B两点，点A在第二象限，且点A的横坐标为－1，作AD⊥x轴，垂足为D，已知△AOD的面积为2．
(1)写出该反比例函数的关系式；
(2)求出点B的坐标；
(3)若点C的坐标为(3，0)，求△ABC的面积．
例三、已知y=y1+y2 ,y1与ｘ＋1成正比例，ｙ2与ｘ＋1成反比例，当ｘ＝0时，ｙ＝－5；当ｘ＝2时，ｙ＝－7。
（1）求ｙ与ｘ的函数关系式；
（2）当ｙ＝5时，求ｘ的值。
例四、如图，直线y=kx+b与反比例函数(x＜0)的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为(－2，4)，点B的横坐标为－4．
(1)试确定反比例函数的关系式； (2)求△AOC的面积．
例五、如图，一次函数y=－x+8和反比例函数的图象在第一象限内有两个不同的公共点A(x 1，y 1)、B(x2，y 2)．
(1)求实数k的取值范围． (2)若△AOB的面积S△AOB=24，求k的值．
例六、如图，正方形OABC的面积为4，点O为坐标原点，点B在函数(k＜0，x＜0)的图象上，点P(m，n)是函数(k＜0，x＜0)的图象上异于点B的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F．
(1)设矩形OEPF的面积为S 1，判断S 1与点P的位置是否有关(不必说理由)．
(2)从矩形OEPF的面积中减去其与正方形OABC重合的面积，剩余面积记为S 2，写
出S 2与m的函数关系式，并标明m的取值范围．
图5
例七、如图5，已知一次函数的图象与轴、轴分别交于A、B两点，且与反比例函数的图象在第一象限交于C点，CD垂直于轴，垂足为D，若OA＝OB＝OD＝1.
（1）求点A、B、D的坐标；（2）求一次函数和反比例函数的解析式.
例八、如图，已知A（﹣4，），B（﹣1，2）是一次函数y=kx+b与反比例函数y=（m≠0，m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．
（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．
拓展应用：
1．下列函数中，属于反比例函数的是 （ ）
A．y＝x－1B．C．D．
2．(2012．哈尔滨)如果反比例函数y＝的图象经过点(－1，－2)，那么k的值是（ ）
A．2 B．－2 C．－3 D．3
3．反比例函数y＝－的图象大致是（ ）
4．两位同学在描述同一个反比例函数的图象时，甲同学说：“这个反比例函数图象上的任意一点到两坐标轴的距离的积都是3”乙同学说：“这个反比例函数的图象与直线y＝x有两个交点，”你认为这两位同学所描述的反比例函数的关系式应是 ( )
A．B．C．D．
5．反比例函数y＝在第一象限内的图象如图所示，则k的值可能是（ ）
A．1 B．2 C．3 D．4
6．(2012．广州)如图，正比例函数y1＝k1x和反比例函数的图象交于A(－1，2)、B(1，－2)两点．若y1