2019-2020学年广东省佛山市禅城区九上期末数学试卷

这是一份2019-2020学年广东省佛山市禅城区九上期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列函数关系式中，y 是 x 的反比例函数的是
A. y=3xB. y=3x+1C. y=3xD. y=3x2

2. 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是
A. 频率就是概率
B. 频率与试验次数无关
C. 概率是随机的，与频率无关
D. 随着试验次数的增加，频率一般会越来越接近概率

3. 如图所示的几何体为圆台，其俯视图正确的是
A. B.
C. D.

4. 已知两个相似三角形的相似比为 4:9，则这两个三角形的对应高的比为
A. 2:3B. 4:9C. 16:81D. 9:4

5. 将抛物线 y=x2 平移得到抛物线 y=x+22，则这个平移过程是
A. 向上平移 2 个单位长度B. 向下平移 2 个单位长度
C. 向左平移 2 个单位长度D. 向右平移 2 个单位长度

6. 如图，一辆小车沿倾斜角为 α 的斜坡向上行驶 13 米，已知 sinα=513，则小车上升的高度是
A. 5 米B. 6 米C. 6.5 米D. 7 米

7. 已知菱形的周长等于 40 cm，两对角线的比为 3:4，则对角线的长分别是
A. 12 cm，16 cmB. 6 cm，8 cmC. 3 cm，4 cmD. 24 cm，32 cm

8. 已知关于 x 的方程 x2−2x+m=0 有实数根，则 m 的取值范围是
A. m≤1B. m≤−1C. m≥1D. m<1

9. 对于抛物线 y=−12x+12+3，下列结论：
①抛物线的开口向下；
②对称轴为直线 x=1；
③顶点坐标为 −1,3；
④ x>1 时，y 随 x 的增大而减小，
其中正确结论的个数为
A. 1B. 2C. 3D. 4

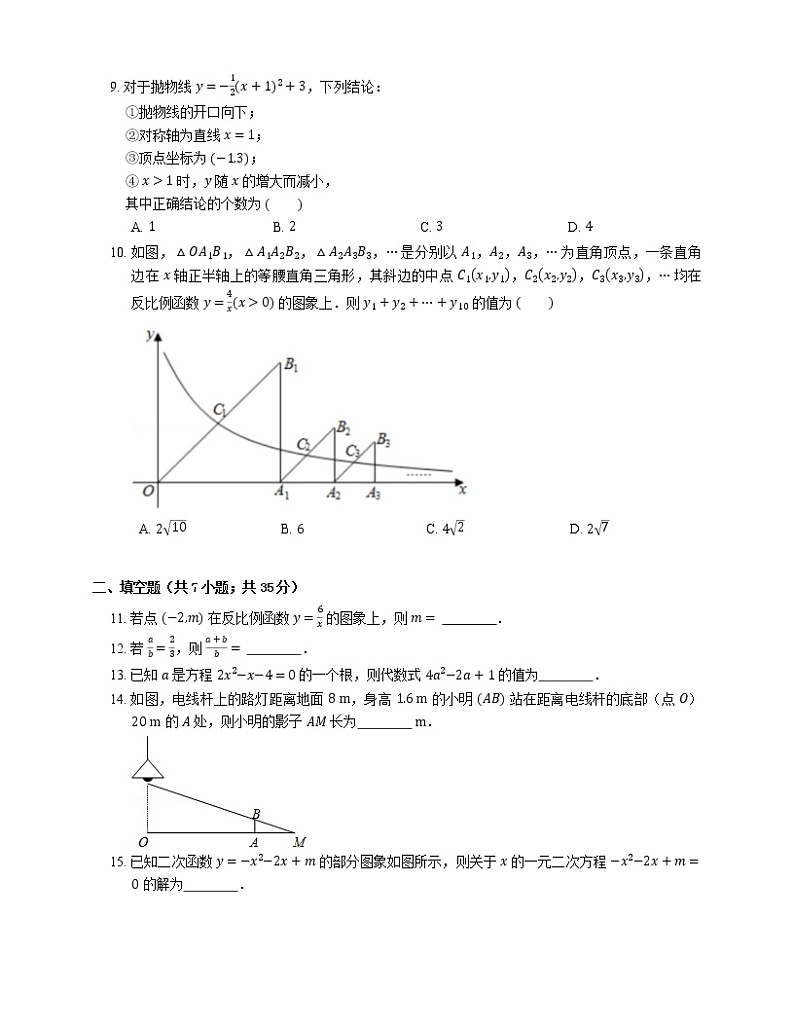
10. 如图，△OA1B1，△A1A2B2，△A2A3B3，⋯ 是分别以 A1，A2，A3，⋯ 为直角顶点，一条直角边在 x 轴正半轴上的等腰直角三角形，其斜边的中点 C1x1,y1，C2x2,y2，C3x3,y3，⋯ 均在反比例函数 y=4xx>0 的图象上．则 y1+y2+⋯+y10 的值为
A. 210B. 6C. 42D. 27

二、填空题（共7小题；共35分）
11. 若点 −2,m 在反比例函数 y=6x 的图象上，则 m= ．

12. 若 ab=23，则 a+bb= ．

13. 已知 a 是方程 2x2−x−4=0 的一个根，则代数式 4a2−2a+1 的值为 ．

14. 如图，电线杆上的路灯距离地面 8 m，身高 1.6 m 的小明 AB 站在距离电线杆的底部（点 O）20 m 的 A 处，则小明的影子 AM 长为 m．

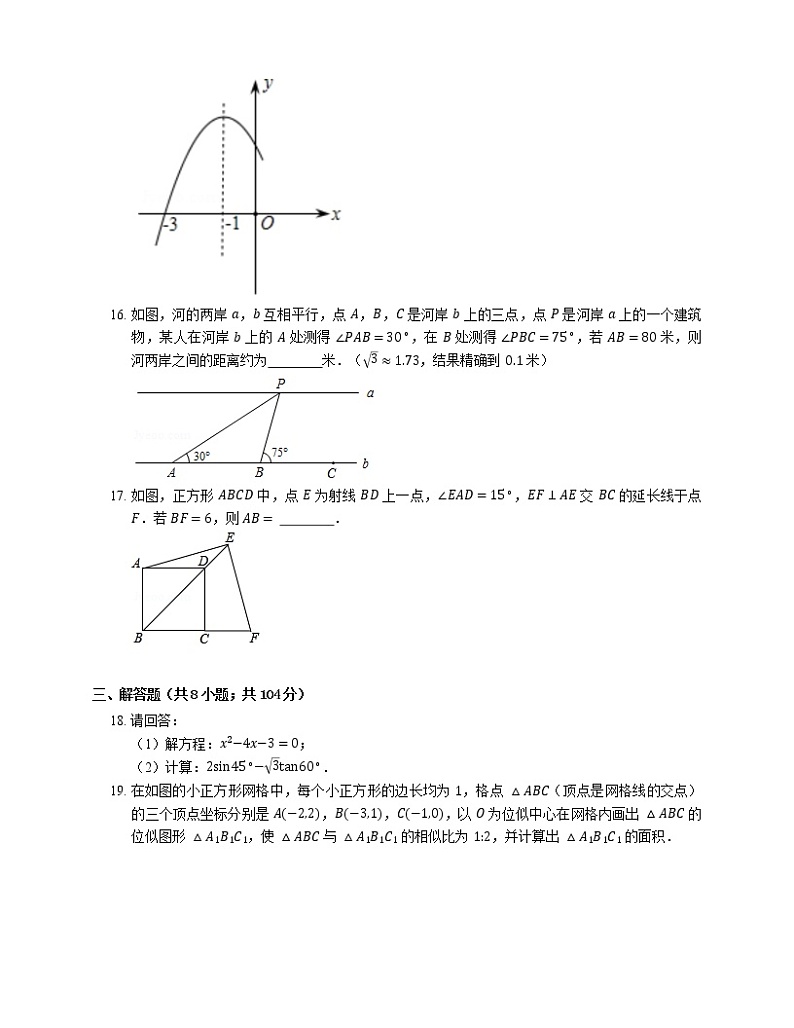
15. 已知二次函数 y=−x2−2x+m 的部分图象如图所示，则关于 x 的一元二次方程 −x2−2x+m=0 的解为 ．

16. 如图，河的两岸 a，b 互相平行，点 A，B，C 是河岸 b 上的三点，点 P 是河岸 a 上的一个建筑物，某人在河岸 b 上的 A 处测得 ∠PAB=30∘，在 B 处测得 ∠PBC=75∘，若 AB=80 米，则河两岸之间的距离约为 米．（3≈1.73，结果精确到 0.1 米）

17. 如图，正方形 ABCD 中，点 E 为射线 BD 上一点，∠EAD=15∘，EF⊥AE 交 BC 的延长线于点 F．若 BF=6，则 AB= ．

三、解答题（共8小题；共104分）
18. 请回答：
（1）解方程：x2−4x−3=0；
（2）计算：2sin45∘−3tan60∘．

19. 在如图的小正方形网格中，每个小正方形的边长均为 1，格点 △ABC（顶点是网格线的交点）的三个顶点坐标分别是 A−2,2，B−3,1，C−1,0，以 O 为位似中心在网格内画出 △ABC 的位似图形 △A1B1C1，使 △ABC 与 △A1B1C1 的相似比为 1:2，并计算出 △A1B1C1 的面积．

20. 如图，在等腰三角形 ABC 中，AB=AC，AH⊥BC，点 E 是 AH 上一点，延长 AH 至点 F，使 FH=EH．求证：四边形 EBFC 是菱形．

21. 某公司 2017 年产值 2500 万元，2019 年产值 3025 万元．
（1）求 2017 年至 2019 年该公司产值的年平均增长率；
（2）由（1）所得结果，预计 2020 年该公司产值将达多少万元?

22. 学校实施新课程改革以来，学生的学习能力有了很大提高．王老师为进一步了解本班学生自主学习、合作交流的现状，对该班部分学生进行调查，把调查结果分成四类（A：特别好，B：好，C：一般，D：较差）后，再将调查结果绘制成两幅不完整的统计图（如图）．请根据统计图解答下列问题：
（1）本次调查中，王老师一共调查了 名学生；
（2）将条形统计图补充完整；
（3）为了共同进步，王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习，请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率．

23. 已知一次函数 y=−2x+b（b 为常数，b>0）的图象分别与 x 轴、 y 轴交于 A，B 两点，且与反比例函数 y=−4x 图象交于 C，D 两点（点 C 在第二象限内），过点 C 作 CE⊥x 轴于点 E．
（1）求 tan∠ACE 的值；
（2）记 S1 为四边形 CEOB 的面积，S2 为 △OAB 的面积，若 S1S2=79，求 b 的值．

24. 如图，折叠边长为 a 的正方形 ABCD，使点 C 落在边 AB 上的点 M 处（不与点 A，B 重合），点 D 落在点 N 处，折痕 EF 分别与边 BC，AD 交于点 E，F，MN 与边 AD 交于点 G．证明：
（1）△AGM∽△BME；
（2）若 M 为 AB 中点，则 AM3=AG4=MG5；
（3）△AGM 的周长为 2a．

25. 如图，三角形 ABC 是以 BC 为底边的等腰三角形，点 A，C 分别是一次函数 y=−34x+3 的图象与 y 轴、 x 轴的交点，点 B 在二次函数 y=18x2+bx+c 的图象上，且该二次函数图象上存在一点 D，使四边形 ABCD 能构成平行四边形．
（1）试求 b，c 的值，并写出该二次函数表达式；
（2）动点 P 沿线段 AD 从 A 到 D，同时动点 Q 沿线段 CA 从 C 到 A 都以每秒 1 个单位的速度运动，问：
①当 P 运动过程中能否存在 PQ⊥AC?如果不存在请说明理由；如果存在请说明点的位置?
②当 P 运动到何处时，四边形 PDCQ 的面积最小?此时四边形 PDCQ 的面积是多少?
答案
第一部分
1. C【解析】A、 y=3x 是正比例函数，故此选项不合题意；
B、 y=3x+1 是一次函数，故此选项不合题意；
C、 y=3x 是反比例函数，故此选项符合题意；
D、 y=3x2 是二次函数，故此选项不合题意；
故选：C．
2. D【解析】∵ 大量重复试验事件发生的频率逐渐稳定到某个常数附近，可以用这个常数估计这个事件发生的概率，
∴ D选项说法正确．故选：D．
3. C【解析】从几何体的上面看所得到的图形是两个同心圆，故选：C．
4. B【解析】因为两个相似三角形的相似比为 4:9，
所以则这两个三角形的对应高的比为 4:9．
5. C
【解析】将抛物线 y=x2 平移得到抛物线 y=x+22，则这个平移过程正确的是向左平移了 2 个单位，故选：C．
6. A【解析】如图 AC=13，作 CB⊥AB，
∵sinα=513=CBAC，
∴BC=5，
∴ 小车上升的高度是 5 m．
7. A【解析】菱形的周长为 40 cm，则菱形的边长为 10 cm，菱形的对角线互相垂直，所以 △ABO 为直角三角形，
设菱形的对角线长为 2x，2y，则 x:y=3:4，
在 Rt△ABO 中，x2+y2=102，
解得 x=6 cm，y=8 cm，
故对角线长为 12 cm，16 cm．
8. A【解析】由题意知，Δ=4−4m≥0，
∴m≤1．
9. C【解析】① ∵a=−12<0，
∴ 抛物线的开口向下，正确；
②对称轴为直线 x=−1，故本小题错误；
③顶点坐标为 −1,3，正确；
④ ∵x>−1 时，y 随 x 的增大而减小，
∴x>1 时，y 随 x 的增大而减小一定正确；
综上所述，结论正确的个数是①③④共 3 个．
10. A
【解析】过 C1，C2，C3⋯ 分别作 x 轴的垂线，垂足分别为 D1，D2，D3⋯，
则 ∠OD1C1=∠OD2C2=∠OD3C3=90∘，
∵ 三角形 OA1B1 是等腰直角三角形，
∴∠A1OB1=45∘，
∴∠OC1D1=45∘，
∴OD1=C1D1，
其斜边的中点 C1 在反比例函数 y=4x，
∴C2,2，即 y1=2，
∴OD1=D1A1=2，
∴OA1=2OD1=4，
设 A1D2=a，则 C2D2=a，此时 C24+a,a，
代入 y=4x 得：a4+a=4，
解得：a=22−2，即：y2=22−2，
同理：y3=23−22，y4=24−23，⋯⋯
∴y1+y2+⋯+y10=2+22−2+23−22+⋯⋯210−29=210．
第二部分
11. −3
【解析】将点 −2,m 代入反比例函数 y=6x 得，m=6−2=−3．
12. 53
【解析】根据等式的性质：两边都加 1，ab+1=23+1，则 a+bb=53．
13. 9
【解析】因为 a 是方程 2x2=x+4 的一个根，
所以 2a2−a=4，
所以 4a2−2a+1=22a2−a+1=2×4+1=9．
14. 5
【解析】由题意得，AMAM+OA=AB8，
即 AMAM+20=1.68，解得：AM=5．
15. x1=−3，x2=1
【解析】根据图象可知，二次函数 y=−x2−2x+m 的部分图象经过点 −3,0，
所以该点适合方程 y=−x2−2x+m，代入，得 −32+2×−3+m=0，
解得，m=3, ⋯⋯①
把 ① 代入一元二次方程 −x2−2x+m=0，
得 −x2−2x+3=0, ⋯⋯②
解 ②，得 x1=−3，x2=1，
所以关于 x 的一元二次方程 −x2−2x+m=0 的解为 x1=−3，x2=1．
16. 54.6
【解析】过点 A 作 AE⊥a 于点 E，过点 B 作 BD⊥PA 于点 D，
∵∠PBC=75∘，∠PAB=30∘，
∴∠DPB=45∘，
∵AB=80，
∴BD=40，AD=403，
∴PD=DB=40，
∴AP=AD+PD=403+40，
∵a∥b，
∴∠EPA=∠PAB=30∘，
∴AE=12AP=203+20≈54.6．
17. 23
【解析】连接 AC 交 BD 于 O，作 FG⊥BE 于 G，如图所示：
则 ∠BGF=∠EGF=90∘，
∵ 四边形 ABCD 是正方形，
∴AC⊥BD，OA=OB=OC=OD，∠ADB=∠CBG=45∘，
∴△BFG 是等腰直角三角形，
∴BG=FG=22BF=32，
∵∠ADB=∠EAD+∠AED，∠EAD=15∘，
∴∠AED=30∘，
∴OE=3OA，
∵EF⊥AE，
∴∠FEG=60∘，
∴∠EFG=30∘，
∴EG=33FG=6，
∴BE=BG+EG=32+6，
∵BE=OB+OE，
∴OA+3AO=32+6，解得：OA=6，
∴AB=2OA=23．
第三部分
18. （1） 因为
x2−4x=3.
所以
x2−4x+4=3+4.
即
x−22=7.
则
x−2=±7.
解得
x=2±7.
（2） 原式=2×22−3×3=2−3.
19. 如图所示：△A1B1C1，即为所求．
△A1B1C1 的面积为：4×4−12×2×4−12×2×2−12×2×4=6．
20. ∵AB=AC，AH⊥CB，
∴BH=HC，
∵FH=EH，
∴ 四边形 EBFC 是平行四边形，
又 ∵AH⊥CB，
∴ 四边形 EBFC 是菱形．
21. （1） 设 2017 年至 2019 年该公司产值的年平均增长率为 x．
依题意，得：
25001+x2=3025.
解得：
x1=0.1=10%,x2=−2.1不合题意,舍去.
答：2017 年至 2019 年该公司产值的年平均增长率为 10%．
（2） 3025×1+10%=3327.5（万元）．
答：由（1）所得结果，预计 2020 年该公司产值将达 3327.5 万元．
22. （1） 20
【解析】根据题意得：王老师一共调查学生：2+1÷15%=20（名）．
（2） 因为C类女生：20×25%−2=3（名）；
D类男生：20×1−15%−50%−25%−1=1（名）；
如图：
（3） 列表如下：A类中的两名男生分别记为 A1 和 A2，
男A1男A2女A男D男A1男D男A2男D女A男D女D男A1女D男A2女D女A女D
共有 6 种等可能的结果，其中，一男一女的有 3 种，
所以所选两位同学恰好是一位男生和一位女生的概率为：36=12．
23. （1） 一次函数 y=−2x+b（b 为常数，b>0）的图象分别与 x 轴、 y 轴交于 A，B 两点，
令 x=0，则 y=b；令 y=0，则求得 x=b2，
∴Ab2,0，B0,b，
∴OA=b2，OB=b，
在 Rt△AOB 中，tan∠ABO=OAOB=b2b=12，
∵CE⊥x 轴于点 E，
∴CE∥y 轴，
∴∠ACE=∠ABO，
∴tan∠ACE=12．
（2） 根据题意得：S△AOBS△AEC=916=OB2CE2，
∴OBCE=34．
设点 C 的坐标为 x,−2x+b，则 OB=b，CE=−2x+b，
∴b−2x+b=34,−2x+b=−4x, 解得：b=32，或 b=−32（舍去）．
24. （1） ∵ 四边形 ABCD 是正方形，
∴∠A=∠B=∠C=90∘，
∴∠AMG+∠AGM=90∘，
∵EF 为折痕，
∴∠GME=∠C=90∘，
∴∠AMG+∠BME=90∘，
∴∠AGM=∠BME，
在 △AGM 与 △BME 中，
∵∠A=∠B，∠AGM=∠BME，
∴△AGM∽△BME．
（2） ∵M 为 AB 中点，
∴BM=AM=a2，
设 BE=x，则 ME=CE=a−x，
在 Rt△BME 中，∠B=90∘，
∴BM2+BE2=ME2，即 a22+x2=a−x2，
∴x=38a，
∴BE=38a，ME=58a，
由（1）知，△AGM∽△BME，
∴AGBM=GMME=AMBE=43，
∴AG=43BM=23a，GM=43ME=56a，
∴AM3=AG4=MG5．
（3） 设 BM=x，则 AM=a−x，ME=CE=a−BE，
在 Rt△BME 中，∠B=90∘，
∴BM2+BE2=ME2，即 x2+BE2=a−BE2，解得：BE=a2−x22a，
由（1）知，△AGM∽△BME，
∴C△AGMC△BME=AMBE=2aa+x，
∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x，
∴C△AGM=C△BME⋅AMBE=a+x⋅2aa+x=2a．
25. （1） 由 y=−34x+3，
令 x=0，得 y=3，
∴ 点 A0,3；
令 y=0，得 x=4，
∴ 点 C4,0，
∵△ABC 是以 BC 为底边的等腰三角形，
∴B 点坐标为 −4,0，
又 ∵ 四边形 ABCD 是平行四边形，
∴D 点坐标为 8,3，
将点 B−4,0 、点 D8,3 代入二次函数 y=18x2+bx+c，
∴2−4b+c=0,8+8b+c=3, 解得：b=−14,c=−3,
故该二次函数解析式为：y=18x2−14x−3．
（2） ∵OA=3，OB=4，
∴AC=5．
①设点 P 运动了 t 秒时，PQ⊥AC，
此时 AP=t，CQ=t，AQ=5−t，
∵PQ⊥AC，
∴∠AQP=∠AOC=90∘，∠PAQ=∠ACO，
∴△APQ∽△CAO，
∴APAC=AQCO，即 t5=5−t4，解得：t=259．
即当点 P 运动到距离 A 点 259 个单位长度处，有 PQ⊥AC．
② ∵S四边形PDCQ+S△APQ=S△ACD，且 S△ACD=12×8×3=12，
∴ 当 △APQ 的面积最大时，四边形 PDCQ 的面积最小，
当动点 P 运动 t 秒时，AP=t，CQ=t，AQ=5−t，
设 △APQ 底边 AP 上的高为 h，作 QH⊥AD 于点 H，
由 △AQH∽△CAO 可得：h3=5−t5，解得：h=355−t，
∴S△APQ=12t×355−t=310−t2+5t=−310t−522+158.
∴ 当 t=52 时，S△APQ 达到最大值 158，此时 S四边形PDCQ=12−158=818．
故当点 P 运动到距离点 A52 个单位处时，四边形 PDCQ 面积最小，最小值为 818．