浙教版九年级上册2.2 简单事件的概率课时训练

这是一份浙教版九年级上册2.2 简单事件的概率课时训练，文件包含22简单事件的概率第1课时docx、22简单事件的概率第2课时docx等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。
用树状图或列表法计算概率．
当遇到求不是等可能发生事件的概率时，要先转化为每个事件发生的可能性的大小相等．
A组 基础训练
1．(广西中考)从－2，－1，2这三个数中任取两个不同的数相乘，积为正数的概率是( )
A.eq \f(2,3) B.eq \f(1,2) C.eq \f(1,3) D.eq \f(1,4)
2．(济南中考)学校新开设了航模、彩绘、泥塑三个社团，如果征征、舟舟两名同学每人随机选择参加其中一个社团，那么征征和舟舟选到同一社团的概率为( )
A.eq \f(2,3) B.eq \f(1,2) C.eq \f(1,3) D.eq \f(1,4)
3．(海南中考)三张外观相同的卡片分别标有数字1、2、3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是( )
A.eq \f(1,3) B.eq \f(2,3) C.eq \f(1,6) D.eq \f(1,9)
4．从1到6的自然数中，任取两个数相减，它们的差为奇数的概率为( )
A.eq \f(3,5) B.eq \f(1,2) C.eq \f(2,5) D.eq \f(1,5)
5．有两道门，各配有2把钥匙．这4把钥匙分放在2个抽屉里，使每个抽屉里恰好有每一道门的1把钥匙，若从每个抽屉里任取1把钥匙，则能打开两道门的概率是________．
6．(杭州中考)一个仅装有球的不透明布袋里共有3个球(只有颜色不同)，其中2个是红球，1个是白球，从中任意摸出一个球，记下颜色后放回，搅匀，再任意摸出一个球，则两次摸出都是红球的概率是________．
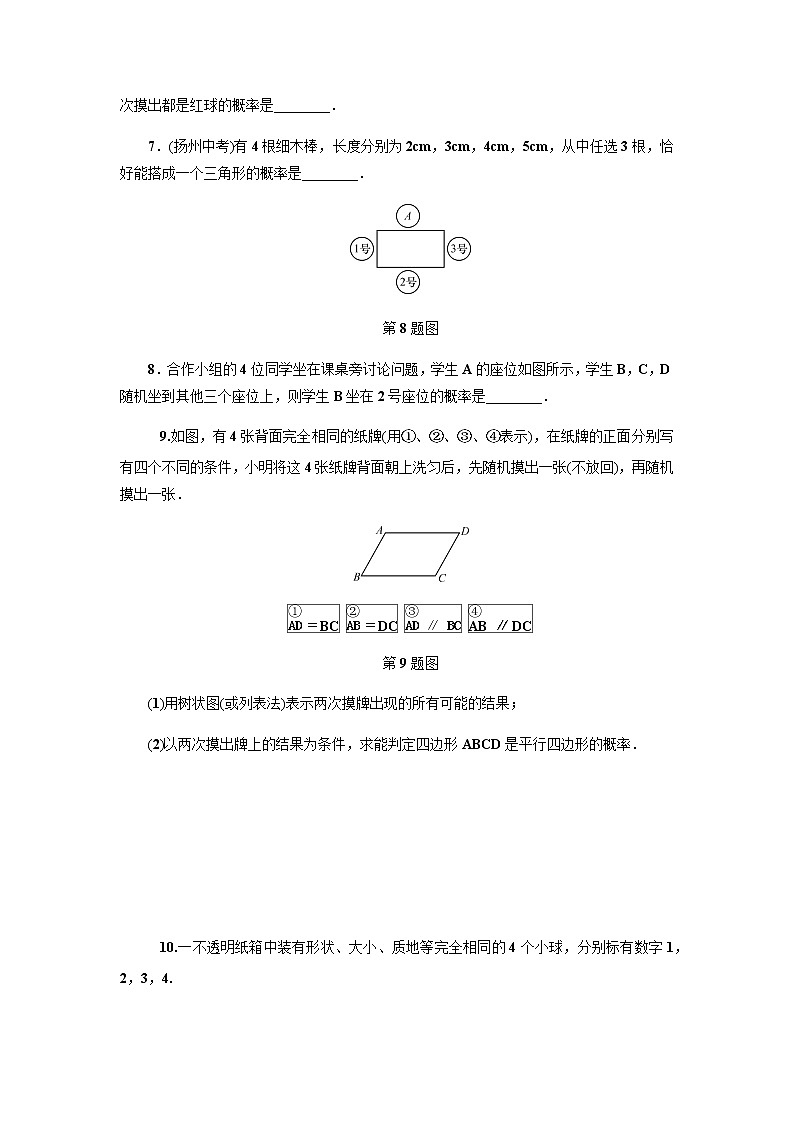
7．(扬州中考)有4根细木棒，长度分别为2cm，3cm，4cm，5cm，从中任选3根，恰好能搭成一个三角形的概率是________．
第8题图
8．合作小组的4位同学坐在课桌旁讨论问题，学生A的座位如图所示，学生B，C，D随机坐到其他三个座位上，则学生B坐在2号座位的概率是________．
eq \a\vs4\al()9.如图，有4张背面完全相同的纸牌(用①、②、③、④表示)，在纸牌的正面分别写有四个不同的条件，小明将这4张纸牌背面朝上洗匀后，先随机摸出一张(不放回)，再随机摸出一张．
eq \x(\a\al(①,AD＝BC)) eq \x(\a\al(②,AB＝DC)) eq \x(\a\al(③,AD∥BC)) eq \x(\a\al(④,AB∥DC))
第9题图
(1)用树状图(或列表法)表示两次摸牌出现的所有可能的结果；
(2)以两次摸出牌上的结果为条件，求能判定四边形ABCD是平行四边形的概率．
eq \a\vs4\al()10.一不透明纸箱中装有形状、大小、质地等完全相同的4个小球，分别标有数字1，2，3，4.
(1)从纸箱中随机地一次取出两个小球，求这两个小球上所标的数字一个是奇数另一个是偶数的概率；
(2)先从纸箱中随机地取出一个小球，用小球上所标的数字作为十位上的数字；将取出的小球放回后，再随机地取出一个小球，用小球上所标的数字作为个位上的数字，则组成的两位数恰好能被3整除的概率是多少？试用树状图或列表法加以说明．
B组 自主提高
eq \a\vs4\al()11.(嘉兴中考)红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏，下列命题中错误的是( )
游戏规则：若一人出“剪刀”，另一人出“布”，则出“剪刀”者胜；若一人出“锤子”，另一人出“剪刀”，则出“锤子”者胜；若一人出“布”，另一人出“锤子”，则出“布”者胜．若两人出相同的手势，则两人平局．
第11题图
A．红红不是胜就是输，所以红红胜的概率为eq \f(1,2)
B．红红胜或娜娜胜的概率相等
C．两人出相同手势的概率为eq \f(1,3)
D．娜娜胜的概率和两人出相同手势的概率一样
eq \a\vs4\al()12.(宿迁中考)有2部不同的电影A、B，甲、乙、丙3人分别从中任意选择1部观看．
(1)求甲选择A部电影的概率；
(2)求甲、乙、丙3人选择同1部电影的概率(请用画树状图的方法给出分析过程，并求出结果)．
C组 综合运用
eq \a\vs4\al()13.(朝阳中考)在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．
甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．
(1)甲同学的方案公平吗？请用列表或画树状图的方法说明；
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？(只回答，不说明理由)
参考答案
【课时训练】
1－4.CCAA 5.eq \f(1,2) 6.eq \f(4,9) 7.eq \f(3,4) 8.eq \f(1,3) 9.(1)画树状图如下：
第9题图
(2)∵共有12种等可能的情况，其中能使四边形ABCD是平行四边形的有8种，∴P(能判定四边形ABCD是平行四边形)＝eq \f(8,12)＝eq \f(2,3). 10.(1)从4个球中任取两个共有6种可能：1、2；1、3；1、4；2、3；2、4；3、4.P(一个奇数一个偶数)＝eq \f(4,6)＝eq \f(2,3)； (2)
P(能被3整除)＝P(数字和为3的倍数)＝eq \f(5,16). 11.A 12.(1)甲选择A部电影的概率＝eq \f(1,2)； (2)画树状图为：
第12题图
共有8种等可能的结果数，其中甲、乙、丙3人选择同1部电影的结果数为2，所以甲、乙、丙3人选择同1部电影的概率＝eq \f(2,8)＝eq \f(1,4). 13.(1)甲同学的方案不公平．理由如下：列表法，
所有可能出现的结果共有12种，其中抽出的牌面上的数字之和为奇数的有：8种，故小明获胜的概率为：eq \f(8,12)＝eq \f(2,3)，则小刚获胜的概率为：eq \f(1,3)，故此游戏两人获胜的概率不相同，即甲同学的方案不公平； (2)不公平．理由如下：
所有可能出现的结果共有6种，其中抽出的牌面上的数字之和为奇数的有：4种，故小明获胜的概率为：eq \f(4,6)＝eq \f(2,3)，则小刚获胜的概率为：eq \f(1,3)，故此游戏两人获胜的概率不相同，即乙同学的方案不公平．
十位数字
1
2
3
4
个位数字
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4

小刚
小明
2
3
4
5
2
(2，3)
(2，4)
(2，5)
3
(3，2)
(3，4)
(3，5)
4
(4，2)
(4，3)
(4，5)
5
(5，2)
(5，3)
(5，4)

小刚
小明
2
3
4
2
(2，3)
(2，4)
3
(3，2)
(3，4)
4
(4，2)
(4，3)