2018-2019学年广东省深圳市南山区七上期末数学试卷

这是一份2018-2019学年广东省深圳市南山区七上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 如果 a 与 −3 互为相反数，那么 a 等于
A. −3B. 3C. −13D. 13

2. 在“生命安全”主题教育活动中，为了解甲、乙、丙、丁四所学校学生对生命安全知识掌握情况，小丽制定了如下方案，你认为最合理的是
A. 抽取乙校初二年级学生进行调查
B. 在丙校随机抽取600名学生进行调查
C. 随机抽取150名老师进行调查
D. 在四个学校各随机抽取150名学生进行调査

3. 2018 年俄罗斯世界杯开幕式于 6 月 14 日在莫斯科卢日尼基球场举行，该球场可容纳 81000 名观众，其中数据 81000 用科学记数法表示为
A. 81×103B. 8.1×104C. 8.1×105D. 0.81×105

4. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原来正方体中，与“国”字所在面相对的面上的汉字是
A. 厉B. 害C. 了D. 我

5. 下列运算正确的是
A. 3a2+5a2=8a4B. 5a+7b=12ab
C. 2m2n−5nm2=−3m2nD. 2a−2a=a

6. 下列说法正确的是
A. a 一定是正数， −a 一定是负数
B. −1 是最大的负整数
C. 0 既没有倒数也没有相反数
D. 若 a≠b ，则 a2≠b2

7. 小川今年 5 岁，他爸爸今年 38 岁，几年后他爸爸年龄是小川年龄的 4 倍?设 x 年后爸爸年龄是小川年龄的 4 倍，则可列方程
A. 45+x=38B. 45+x=38+x
C. 4×5+x=38D. 4×5=38+x

8. 下列结论中，正确的是
A. 单项式 3xy27 的系数是 3，次数是 2
B. 单项式 m 的次数是 1，没有系数
C. 单项式 −xy2z 系数是 −1，次数是 4
D. 多项式 5x2−xy+3 是三次三项式

9. 如图是“大润发”超市中“飘柔”洗发水的价格标签，一服务员不小心将墨水滴在标签上，使得原价看不清楚，请你帮忙算一算，该洗发水的原价为
A. 22 元B. 23 元C. 24 元D. 26 元

10. 把一副三角尺 ABC 与 BDE 按如图所示那样拼在一起，其中 A，D，B 三点在同一直线上，BM 为 ∠ABC 的平分线，BN 为 ∠CBE 的平分线，则 ∠MBN 的度数是
A. 30∘B. 45∘C. 55∘D. 60∘

11. 实数 a，b，c 在数轴上的对应点的位置如图所示，则正确的结论是
A. ∣a∣>4B. c−b>0C. ac>0D. a+c>0

12. 将正整数 1 至 2018 按一定规律排列如表：
平移表中带阴影的方框，方框中三个数的和可能是
A. 2019B. 2018C. 2016D. 2013

二、填空题（共4小题；共20分）
13. 如果水位升高 3 m 记作 +3 m，那么水位下降 6 m 记作 m．

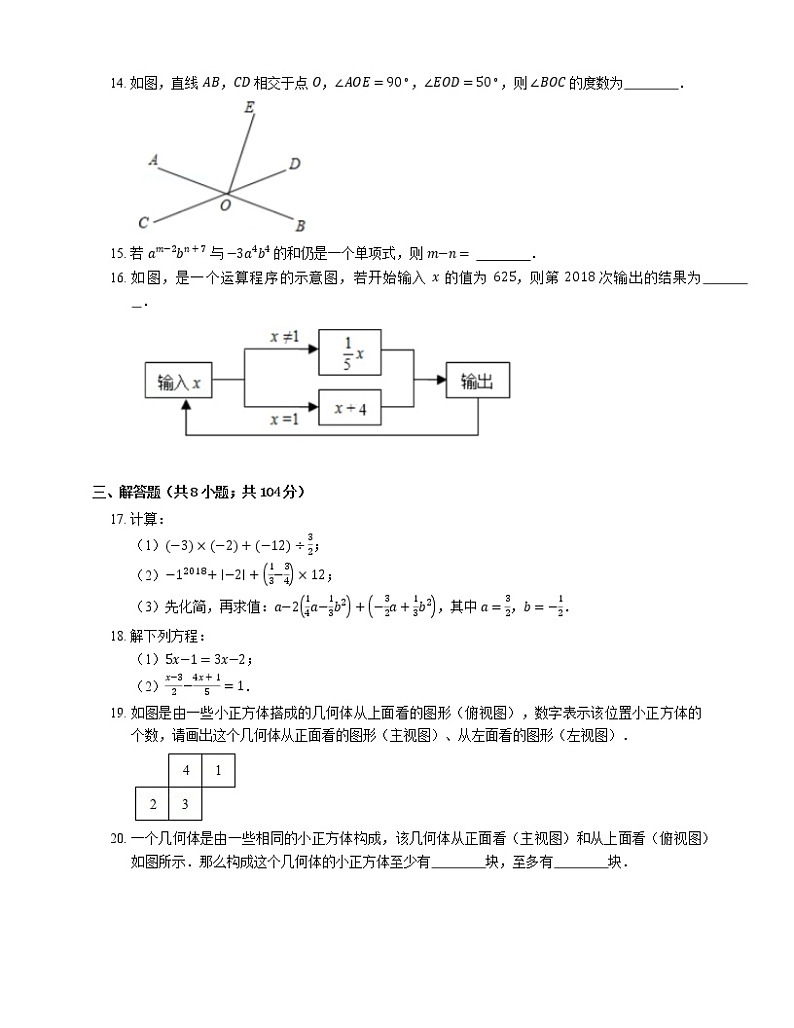
14. 如图，直线 AB，CD 相交于点 O，∠AOE=90∘，∠EOD=50∘，则 ∠BOC 的度数为 ．

15. 若 am−2bn+7 与 −3a4b4 的和仍是一个单项式，则 m−n= ．

16. 如图，是一个运算程序的示意图，若开始输入 x 的值为 625，则第 2018 次输出的结果为 ．

三、解答题（共8小题；共104分）
17. 计算：
（1）−3×−2+−12÷32；
（2）−12018+−2+13−34×12；
（3）先化简，再求值：a−214a−13b2+−32a+13b2，其中 a=32，b=−12．

18. 解下列方程：
（1）5x−1=3x−2；
（2）x−32−4x+15=1．

19. 如图是由一些小正方体搭成的几何体从上面看的图形（俯视图），数字表示该位置小正方体的个数，请画出这个几何体从正面看的图形（主视图）、从左面看的图形（左视图）．

20. 一个几何体是由一些相同的小正方体构成，该几何体从正面看（主视图）和从上面看（俯视图）如图所示．那么构成这个几何体的小正方体至少有 块，至多有 块．

21. 我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”．深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度（程度分为：“A：了解很多”、“B：了解较多”、“C：了解较少”、“D：不了解”），对本市某所中学的学生进行了抽样调查．我们将这次调查的结果绘制了以下两幅不完整统计图：
根据以上信息，解答下列问题：
（1）补全条形统计图．
（2）本次抽样调查了 名学生；在扇形统计图中，求出“D”的部分所对应的圆心角度数．
（3）若该中学共有 2000 名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较少”的有多少人．

22. 甲乙两人在一环形场地上锻炼，甲骑自行车，乙跑步，甲比乙每分钟快 200 m，两人同时从起点同向出发，经过 3 min 两人首次相遇，此时乙还需跑 150 m 才能跑完第一圈．
（1）求甲、乙两人的速度分别是每分钟多少米?（列方程或者方程组解答）
（2）若两人相遇后，甲立即以每分钟 300 m 的速度掉头向反方向骑车，乙仍按原方向继续跑，要想不超过 1.2 min 两人再次相遇，则乙的速度至少要提高每分钟多少米?

23. 如图，点 C 在线段 AB 上，点 M，N 分别是 AC，BC 的中点．
（1）若 AC=9 cm，CB=6 cm，求线段 MN 的长；
（2）若 C 为线段 AB 上任一点，满足 AC+CB=a cm，其它条件不变，你能猜想 MN 的长度吗?请直接写出你的答案．
（3）若 C 在线段 AB 的延长线上，且满足 AC−BC=b cm，M，N 分别为 AC，BC 的中点，你能猜想 MN 的长度吗?请画出图形，写出你的结论，并说明理由．

24. 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为 1 的分数），那么无限循环小数如何表示为分数形式呢?请看以下示例：
例：将 0.7 化为分数形式
由于 0.7=0.777⋯，设 x=0.777, ⋯⋯①
则 10x=7.777. ⋯⋯②
②−① 得 9x=7，解得 x=79，于是得 0.7=79．
同理可得 0.3=39=13，1.4=1+0.4=1+49=139．
根据以上阅读，回答下列问题（以下计算结果均用最简分数表示）．
（1）【基础训练】
（1）0.5= ，5.8= ；
（2）将 0.23 化为分数形式，写出推导过程．
（2）【能力提升】
0.315= ，2.018= ；
（注：0.315=0.315315⋯，2.018=2.01818⋯）
（3）【探索发现】
①试比较 0.9 与 1 的大小：0.9 1（填“>”、“<”或“=”）；
②若已知 0.285714=27，则 3.714285= ．
（注：0.285714=0.285714285714⋯）
答案
第一部分
1. B【解析】∵a 与 −3 互为相反数，
∴a=3．
2. D【解析】【分析】根据抽样调查的具体性和代表性解答即可．
【解析】解：为了解甲、乙、丙、丁四所学校学生对生命安全知识掌握情况，在四个学校各随机抽取150名学生进行调査最具有具体性和代表性，
故选：D．
【点评】此题考查抽样调查，关键是理解抽样调查的具体性和代表性．
3. B【解析】81000=8.1×104．
4. D
5. C
【解析】A、合并同类项系数相加字母及指数不变，故A错误；
B、不是同类项不能合并，故B错误；
C、合并同类项系数相加字母及指数不变，故C正确；
D、合并同类项系数相加字母及指数不变，故D错误．
6. B【解析】A．大于零的数是正数，小于零的数是负数，故A错误；
B． −1 是最大的负整数，故B正确；
C． 0 没有倒数， 0 的相反数是 0 ，故C错误；
D．互为相反数的平方相等，故D错误．
7. B【解析】设 x 年后爸爸年龄是小川年龄的 4 倍．
根据题意得：45+x=38+x．
8. C【解析】A、单项式 3xy27 的系数是 37，次数是 3，故此选项错误；
B、单项式 m 的次数是 1，系数也是 1，故此选项错误；
C、单项式 −xy2z 系数是 −1，次数是 4，正确；
D 、多项式 5x2−xy+3 是二次三项式，故此选项错误．
故选：C．
9. C
10. B
【解析】∵BM 为 ∠ABC 的平分线，
∴∠CBM=12∠ABC=12×60∘=30∘，
∵BN 为 ∠CBE 的平分线，
∴∠CBN=12∠EBC=12×60∘+90∘=75∘，
∴∠MBN=∠CBN−∠CBM=75∘−30∘=45∘．
11. B【解析】∵−4 ∴∣a∣<4．
∴ A不正确；
又 ∵c>b，
∴c−b>0，
∴ B正确；
又 ∵a<0，c>0，
∴ac<0，
∴ C不正确；
又 ∵a<−3，c<3，
∴a+c<0，
∴ D不正确．
12. D【解析】设中间数为 x，则另外两个数分别为 x−1，x+1，
∴ 三个数之和为 x−1+x+x+1=3x．
根据题意得：3x=2019，3x=2018，3x=2016，3x=2013，
解得：x=673，x=67223（舍去），x=672，x=671．
∵673=84×8+1，
∴2019 不合题意，舍去；
∵672=84×8，
∴2016 不合题意，舍去；
∵671=83×8+7，
∴ 三个数之和为 2013．
第二部分
13. −6
【解析】水位升高 3 m 时水位变化记作 +3 m，那么水位下降 6 m 记作 −6 m．
14. 140∘
【解析】∵ 直线 AB，CD 相交于点 O，∠EOA=90∘，
∵∠EOD=50∘，
∴∠BOD=40∘，则 ∠BOC 的度数为：180∘−40∘=140∘．
15. 9
【解析】∵am−2bn+7 与 −3a4b4 的和仍是一个单项式，
∴m−2=4，n+7=4，
解得：m=6，n=−3，
故 m−n=6−−3=9．
16. 1
【解析】当 x=625 时，15x=125，
当 x=125 时，15x=25，
当 x=25 时，15x=5，
当 x=5 时，15x=1，
当 x=1 时，x+4=5，
当 x=5 时，15x=1，
当 x=1 时，x+4=5，
当 x=5 时，15x=1，
⋯
2018−3÷2=1007.5，
即输出的结果是 1．
第三部分
17. （1） 原式=6−12×23=6−8=−2.
（2） 原式=−1+2+4−9=−4.
（3） 原式=a−12a+23b2−32a+13b2=−a+b2.
当 a=32，b=−12 时，
原式=−32+14=−54.
18. （1） 移项得：
5x−3x=−2+1,
合并同类项得：
2x=−1,
系数化为 1，得：
x=−12.
（2） 方程两边同时乘以 10 得：
5x−3−24x+1=10,
去括号得：
5x−15−8x−2=10,
移项得：
5x−8x=10+2+15,
合并同类项得：
−3x=27,
系数化为 1 得：
x=−9.
19. 这个几何体从正面看的图形（主视图），从左面看的图形（左视图）如图所示：
20. 5；7
【解析】如图所示，
由图知构成这个几何体的小正方体至少有 5 块，至多有 7 块．
21. （1） ∵ 被调查的学生总人数为 30÷30%=100（人），
则C对应的人数为 100−30+45+5=20（人），
补全图形如下：
（2） 100；
则扇形统计图中，“D”的部分所对应的圆心角度数为 360∘×5100=18∘．
【解析】由（1）知本次抽样调查了 100 名学生．
（3） 估计这所中学的所有学生中，对“节约教育”内容“了解较少”的有 2000×20100=400（名）．
22. （1） 设乙的速度是每分钟 x 米，则甲的速度是每分钟 x+200 米，
依题意有
3x+150=200×3.
解得
x=150.x+200=150+200=350
．
答：甲的速度是每分钟 350 米，乙的速度是每分钟 150 米．
（2） 200×3−300×1.2÷1.2=600−360÷1.2=240÷1.2=200（米），
200−150=50（米）．
答：乙的速度至少要提高每分钟 50 米．
23. （1） ∵M，N 分别是 AC，BC 的中点，
∴MC=12AC，CN=12BC，
∵AC=9 cm，CB=6 cm，
∴MN=MC+CN=12AC+12BC=12AC+BC=129+6=7.5 cm.
（2） 12a cm
【解析】∵M，N 分别是 AC，BC 的中点，
∴MC=12AC，CN=12BC，
∵AC+CB=a cm，
∴MN=MC+CN=AC+CB=acm=12acm．
（3） MN=12b，
如图，
∵M，N 分别是 AC，BC 的中点，
∴MC=12AC，CN=12BC，
∵AC−BC=b cm，
∴MN=MC−CN=12AC−12BC=12AC−BC=12b．
24. （1） （1）59；539；
（2）0.23=0.232323⋯⋯，
设 x=0.232323,⋯⋯①
则 100x=23.2323,⋯⋯②
②−①，得：99x=23，解得：x=2399，
∴0.23=2399．
【解析】（1）由题意知 0.5=59，5.8=5+89=539．
（2） 35111；11155
【解析】同理 0.315=315999=35111，2.018=2+110×1899=11155．
（3） =；267
【解析】① 0.9=99=1；
② 3.714285+0.285714=3.9=4，
∴4−0.285714=4−27=267．