2018-2019学年天津市和平区八下期末数学试卷

这是一份2018-2019学年天津市和平区八下期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 若 2a+3 在实数范围内有意义，则 a 的取值范围是
A. a≥−32B. a≤−32C. a>−32D. a<−32

2. 如图，在矩形 ABCD 中，对角线 AC 、 BD 相交于点 O，若 OA=2，则 BD 的长为
A. 4B. 3C. 2D. 1

3. 已知直线 y=2x−b 经过点 1,−1，则 b 的值为
A. 3B. −3C. 0D. 6

4. 设矩形的面积为 S，相邻两边长分别为 a，b，已知 S=23，b=10，则 a 等于
A. 230B. 305C. 306D. 35

5. 下列说法正确的是
A. 四个角都相等的四边形是正方形
B. 四条边都相等的四边形是正方形
C. 对角线相等的平行四边形是正方形
D. 对角线互相垂直的矩形是正方形

6. 若直角三角形两条直角边长分别为 2 和 3，则该直角三角形斜边上的高为
A. 13B. 31313C. 61313D. 121313

7. 晨光中学规定学生的学期体育成绩满分为 100 分，其中早练及体育课外活动占 20%，期中考试成绩占 30%，期末考试成绩占 50%．小桐的三项成绩（百分制）依次为 95 分、 90 分、 86 分，则小桐这学期的体育成绩是
A. 88 分B. 89 分C. 90 分D. 91 分

8. 改革开放 40 年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的 2017 年和 2018 年我市居民人均教育、文化和娱乐消费支出的折线图．
说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如 2018 年第二季度与 2017 年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如 2018 年第二季度与 2018 年第一季度相比较．
根据上述信息，下列结论中错误的是
A. 2017 年第二季度环比有所提高B. 2017 年第三季度环比有所提高
C. 2018 年第一季度同比有所提高D. 2018 年第四季度同比有所提高

9. 如图，直线 y=kx+b 过 A−1,2，B−2,0 两点，则 0≤kx+b≤−2x 的解集为
A. x≤−2 或 x≥−1B. 0≤y≤2
C. −2≤x≤0D. −2≤x≤−1

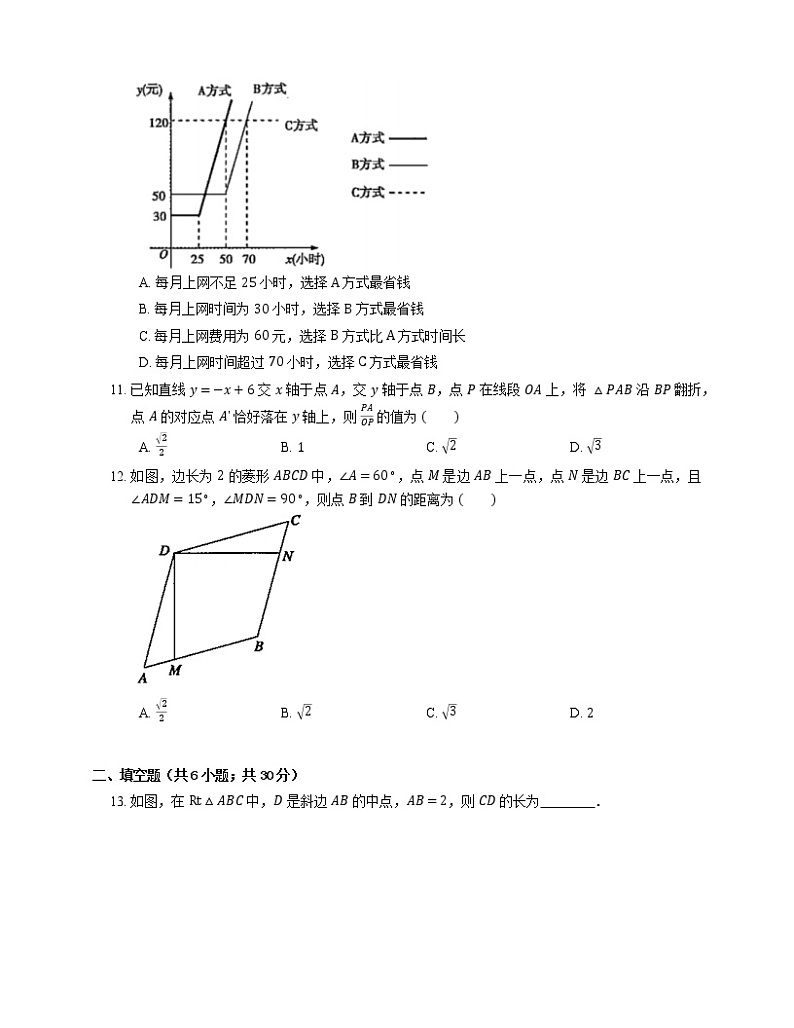
10. 某通信公司推出三种上网月收费方式，这三种收费方式每月所收的费用 y（元）与上网时间 x（小时）的函数关系如图所示，则下列判断错误的是
A. 每月上网不足 25 小时，选择 A 方式最省钱
B. 每月上网时间为 30 小时，选择 B 方式最省钱
C. 每月上网费用为 60 元，选择 B 方式比 A 方式时间长
D. 每月上网时间超过 70 小时，选择 C 方式最省钱

11. 已知直线 y=−x+6 交 x 轴于点 A，交 y 轴于点 B，点 P 在线段 OA 上，将 △PAB 沿 BP 翻折，点 A 的对应点 Aʹ 恰好落在 y 轴上，则 PAOP 的值为
A. 22B. 1C. 2D. 3

12. 如图，边长为 2 的菱形 ABCD 中，∠A=60∘，点 M 是边 AB 上一点，点 N 是边 BC 上一点，且 ∠ADM=15∘，∠MDN=90∘，则点 B 到 DN 的距离为
A. 22B. 2C. 3D. 2

二、填空题（共6小题；共30分）
13. 如图，在 Rt△ABC 中，D 是斜边 AB 的中点，AB=2，则 CD 的长为 ．

14. 农科院对甲、乙两个品种甜玉米各用 10 块试验田进行试验，得到甲、乙两个品种每公顷的平均产量相同，而甲、乙两个品种产量的方差分别为 S甲2≈0.01，S乙2≈0.002，则产量较为稳定的品种是 （填“甲”或“乙”）．

15. 计算 5+35−3 的结果等于 ．

16. 已知一次函数 y=x+b 的图象经过第一、二、三象限，写出一个符合条件的 b 的值为 ．

17. 一个装有进水管与出水管的容器，从某时刻起只打开进水管进水，经过一段时间，再打开出水管放水，至 12 分钟时关停进水管．每分的进水量和出水量是两个常数．在打开进水管到关停进水管这段时间内，容器内的水量 y（单位：升）与时间 x（单位：分）之间的函数关系如图所示，关停进水管后，经过 分钟，容器中的水恰好放完．

18. 图中的虚线网格是等边三角形网格，它的每一个小三角形都是边长为 1 的等边三角形．
（1）如图①，连接相邻两个小正三角形的顶点 A，B，则 AB 的长为 ；
（2）在如图②所示的网格中，用无刻度的直尺，画一个斜边长为 23 的直角三角形，且它的三个顶点都在网格顶点上．

三、解答题（共7小题；共91分）
19. 计算：
（1）212−613+348．
（2）2+32+5．

20. 如图，在四边形 ABCD 中，AB=AD=2，∠A=90∘，∠CBD=30∘，∠C=45∘，求 BD 及 CD 的长．

21. 某校九年级有 1200 名学生，在体育考试前随机抽取部分学生进行跳绳测试，根据测试成绩制作了下面两个统计图．请根据相关信息，解答下列问题：
（1）本次参加跳绳测试的学生人数为 ，图 1 中 m 的值为 ；
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校九年级跳绳测试中得 3 分的学生约有多少人?

22. 在菱形 ABCD 中，AC 是对角线．
（1）如图①，若 AB=6，则菱形 ABCD 的周长为 ；若 ∠DAB=70∘，则 ∠D 的度数是 ；∠DCA 的度数是 ；
（2）如图②，P 是 AB 上一点，连接 DP 交对角线 AC 于点 E，连接 EB，求证 ∠APD=∠EBC．

23. 现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过 1 千克的，按每千克 22 元收费；超过 1 千克，超过的部分按每千克 15 元收费，乙公司表示：按每千克 16 元收费，另加包装费 3 元．设小明快递物品 x 千克．
（1）根据题意，填写如表：
快递物品重量千克0.5134⋯甲公司收费元 22 67⋯乙公司收费元11 51 ⋯
（2）设甲快递公司收费 y1 元，乙快递公司收费 y2 元，分别写出 y1，y2 关于 x 的函数关系式；
（3）当 x>3 时，小明应选择哪家快递公司更省钱?请说明理由．

24. 已知，在正方形 ABCD 中，点 E 在边 AD 上，点 F 在边 BC 的延长线上，且 AE=CF，连接 AC，EF．
（1）如图①，求证 EF∥AC；
（2）如图②，EF 与边 CD 交于点 G，连接 BG，BE，
①求证：△BAE≌△BCG；
②若 BE=EG=4，求 △BAE 的面积．

25. 已知，直线 y=2x−2 与 x 轴交于点 A，与 y 轴交于点 B．
（1）如图 ①，点 A 的坐标为 ，点 B 的坐标为 ；
（2）如图 ②，点 C 是直线 AB 上不同于点 B 的点，且 CA=AB．
① 求点 C 的坐标；
② 过动点 Pm,0 且垂直于 x 轴的直线与直线 AB 交于点 E，若点 E 不在线段 BC 上，则 m 的取值范围是 ；
（3）若 ∠ABN=45∘，求直线 BN 的解析式．
答案
第一部分
1. A
2. A
3. A
4. B
5. D
6. C
7. B
8. C【解析】2017 年第二季度支出 948 元，第一季度支出 859 元，所以第二季度比第一季度提高，故A正确；
2017 年第三季度支出 1113 元，第二季度支出 948 元，所以第三季度比第二季度提高，故B正确；
2018 年第一季度支出 839 元，2017 年第一季度支出 859 元，所以 2018 年第一季度同比有所降低，故C错误；
2018 年第四季度支出 1012 元，2017 年第一季度支出 997 元，所以 2018 年第四季度同比有所提高，故D正确．
9. D【解析】由题意得 2=−k+b,0=−2k+b. 解得 k=2,0=4.
故原不等式组可化为 2x+4≥0,2x+4≤−2x. 解集为 −2≤x≤−1．
10. B
【解析】A 方式的解析式为 yA=30,0≤x≤253.6x−60,x>25，
B 方式的解析式为 yB=50,0≤x≤503.5x−125,x>50，
C 方式的解析式为 yC=120，x≥0．
11. C【解析】如图所示，
根据题意，可得 A6,0，B0,6，
所以 OA=OB=6，
又因为 OA⊥OB，
所以 ∠OAB=∠OBA=45∘，
由折叠性质，可得 ∠OAʹP=∠BAO=45∘，
所以 ∠OPAʹ=∠OAʹP=45∘，OP=OAʹ，
所以 PA=PAʹ=2OP，PAOP=2．
12. B【解析】连接 BD，过点 B 作 BH⊥DN 于点 H，
根据菱形相关性质，可知 ∠ADC=120∘，∠BDC=12∠ADC=60∘，
所以 △BDC 为正三角形，BD=CD=2，∠CDN=∠CDA−∠ADM−∠MDN=15∘，∠BDN=∠BDC−∠CDN=45∘，
又因为 BH⊥DN，
所以 ∠DBH=∠BDH=45∘，DH=BH，
又因为 DH2+BH2=BD2=4，
所以 BH=2，
即点 B 到 DN 的距离为 2．
第二部分
13. 1
14. 乙
15. −4
16. 1（答案不唯一）
17. 8
【解析】由 0∼4 分钟的函数图象可知，进水管的速度为 20÷4=5（升/分）；由 4∼12 分钟的函数图象可知，出水管的速度为 5−30−20÷12−4=3.75（升/分）；
所以关停进水管后，经过 30÷3.75=8（分钟），容器中的水恰好放完．
18. （1）3
（2）如图：
第三部分
19. （1） 212−613+348=43−23+123=143.
（2） 2+32+5=2+52+32+15=17+82.
20. 过点 D 作 DE⊥BC 于点 E．
∵∠A=90∘，AB=AD=2，
∵BD=AB2+AD2=22+22=2．
在 Rt△BDE 中，
∵∠CBD=30∘，
∴DE=12BD=12×2=1．
在 Rt△DEC 中，
∵∠C=45∘，
∴∠CDE=90∘−∠C=90∘−45∘=45∘．
∴∠C=∠CDE．
∴CE=DE=1．
∴CD=CE2+DE2=12+12=2．
21. （1） 50；10
（2） 观察条形统计图，
∵ x=2×10+3×5+4×25+5×1050=3.7，
∴ 本次调查获取的样本数据的平均数是 3.7．
∵ 在这组样本数据中，4 出现了 25 次，出现的次数最多，
∴ 这组样本数据的众数是 4．
将这组样本数据按照由小到大的顺序排列，其中处于中间位置的两个数都是 4，有 4+42=4，
∴ 这组样本数据的中位数是 4．
（3） ∵ 在 50 名学生中，跳绳测试得（3 分）的学生人数比例为 10%，
∴ 由样本数据，估计该校九年级跳绳测试中得（3 分）的学生人数比例约为 10%，
∴ 1200×10%=120（人）．
答：根据样本数据，估计该校九年级跳绳测试中得（3 分）的学生约有 120 人．
22. （1） 24；110∘；35∘
（2） 因为四边形 ABCD 为菱形，
所以 AB∥CD，BC=CD，∠ACB=∠ACD．
因为 AB∥CD，
所以 ∠APD=∠CDE．
在 △CDE 和 △CBE 中，
BC=DC,∠DCE=∠BCE,CE=CE,
所以 △CDE≌△CBESAS．
所以 ∠CDE=∠CBE．
所以 ∠APD=∠EBC．
23. （1） 11；52；19；67
（2） y1=22x,01，
化简得，y1=22x,01，y2=16x+3．
（3） 当 x>3 时，y1=15x+7，y2=16x+3，
当 15x+7=16x+3 时，解得 x=4；
当 15x+7<16x+3 时，x>4；
当 15x+7>16x+3 时，x<4；
综上所述，当 34 时，选甲家快递公司更省钱．
24. （1） ∵ 四边形 ABCD 是正方形，
∴AE∥CF，
∵AE=CF，
∴ 四边形 ACFE 是平行四边形，
∴EF∥AC．
（2） ① ∵ 四边形 ABCD 是正方形，
∴BA=BC，∠BAE=∠BCG=90∘，
∴∠GCF=90∘，∠1=12∠BCG=45∘，
∵EF∥AC，
∴∠F=∠1=45∘，
∴∠CGF=90∘−∠F=45∘，
∴∠F=∠CGF，
∴CG=CF，
∵AE=CF，
∴AE=CG，
在 △BAE 和 △BCG 中，
BA=BC,∠BAE=∠BCG,AE=CG,
∴△BAE≌△BCG．
② ∵△BAE≌△BCG，
∴BE=BG，
∵BE=EG，
∴BE=BG=EG，
∴△BEG 是等边三角形，
∴∠EBG=60∘，
延长 DA 至点 H，使 AH=AE，连接 BH，过点 H 作 HM⊥BE 于点 M，
∵∠BAE=90∘，
∴∠BAH=90∘，
∴∠BAH=∠BAE，
在 △BAH 和 △BAE 中，
AH=AE,∠BAH=∠BAE,AB=AB,
∴△HAB≌△EAB，
∴∠2=∠3，HB=EB=4，
∵△BAE≌△BCG，
∴∠3=∠4，
∵∠ABC=90∘，∠EBG=60∘，
∴∠3=15∘，
∴∠2=∠3=15∘，
∴∠HBE=30∘，
在 Rt△HBM 中，HM=12HB=2，
∴S△HBE=12BE⋅HM=12×4×2=4，
∴S△BAE=12S△HBE=12×4=2．
25. （1） 1,0；0,−2
（2） ①∵CA=AB，A1,0，B0,−2，
∴xB+xC=2xA，即 xC=2，yB+yC=2yA，即 yC=2，
∴C 的坐标为 2,2；
②m<0 或 m>2
（3） 如图，作 AN⊥AB，使得 AN=AB，作 NH⊥x轴 于点 H，
∵∠ABN=45∘，
∴△ABN 是等腰直角三角形，
∵∠AOB=∠BAN=∠AHN=90∘，
∴∠ABO+∠OAB=90∘，∠HAN+∠OAB=90∘，
∴∠ABO=∠HAN，
在 △OAB 和 △HNA 中，∠BOA=∠AHN,ABO=∠NAH,AB=NA,
∴△OAB≌△HNAAAS，
∴AH=BO=2，OA=NH=1，
∴N3,−1，
设直线 BN 的解析式为 y=kx+b，图象过 B0,−2，N3,−1，
有 b=−2,3k+b=−1,
解得 b=−2,k=13,
∴ 直线 BN 的解析式为 y=13x−2，
当直线 BNʹ⊥BN 时，直线 BNʹ 也满足条件，
∴BNʹ 的解析式为 y=−3x−2，
直线 BN 的解析式为 y=13x−2 或 y=−3x−2．