2018-2019学年山东省青岛市崂山区七上期末数学试卷

这是一份2018-2019学年山东省青岛市崂山区七上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 下列各数中，相反数是 −12 的是
A. −12B. 12C. −2D. 2

2. 在下列调查活动中，适合采取普查方式的是
A. 了解中央电视台《新闻联播》栏目的收视率
B. 了解一批洗衣机的使用寿命
C. 了解某班学生对“本学校校训”的知晓率
D. 了解渤海中鱼的种类

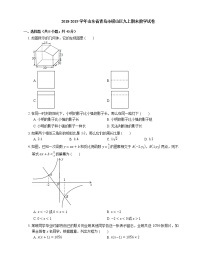
3. 如图，是由 6 个棱长为 1 个单位的正方体摆放而成的，将正方体 A 向右平移 2 个单位，向后平移 1 个单位后，所得几何体的视图 ( )
A. 主视图改变，俯视图改变B. 主视图不变，俯视图不变
C. 主视图不变，俯视图改变D. 主视图改变，俯视图不变

4. 在下列各数中，分数有 个．
−6，0.1234，−512，0.3，0，19，15．
A. 2B. 3C. 4D. 5

5. 若 2x2my3 与 −5xy2n 是同类项，则 ∣m−n∣ 的值是
A. 0B. 1C. 7D. −1

6. 下列运算正确的是
A. −8+3=−11B. −12013×1=−1
C. −52=−25D. −∣−2∣=2

7. 已知线段 AB=8 cm，C 是直线 AB 上的一点，BC=2 cm．若 M 是线段 AB 的中点，N 是线段 BC 的中点，则线段 MN 的长度为
A. 5 cmB. 5 cm 或 3 cmC. 7 cm 或 3 cmD. 7 cm

8. 某城市出租车的收费标准是：起步价 5 元，超过 3 千米后，每行 1 千米加收 2.4 元（不足 1 千米按 1 千米计），某人乘这种出租车从甲地到乙地付款 17 元，那么甲、乙两地的距离应不超过
A. 11 千米B. 5 千米C. 7 千米D. 8 千米

二、填空题（共6小题；共30分）
9. 用一个平面去截一个正方体，如果截去的几何体是一个三棱柱，那么截面的形状一定是 ．

10. 据统计：2018 年 10 月，青岛市全社会用电量为 336900 万度．将 336900 万度这个数据用科学记数法可以表示为 ．

11. 若 x=5 是关于 x 的方程 2x−3m+6=0 的解，则 m 的值等于 ．

12. 崂山区某中学开展以“我最喜欢的职业”为主题的调查活动．通过对学生的随机抽样调查得到一组数据，下面两图（如图）是根据这组数据绘制的两幅不完整的统计图．求在这次活动中“最喜欢的职业”为教师的共 人．

13. 如图，将一个圆分割成三个扇形，若甲、丙两个扇形面积之比为 3:2 ，圆心角 ∠BOC=120∘ ，则 ∠AOC= ∘ ．

14. 如图所示，是一个水平摆放的小正方体木块，图（2），（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第八个叠放的图形中，小正方体木块总数应是 ．

三、解答题（共11小题；共143分）
15. 如图，这是一个由小立方块搭成的几何体从上面看到的形状图，小正方形中的数字表示该位置的小立方块的个数．请你画出它从正面和从左面看到的形状图．

16. 如图所示，已知线段 m，n ， 求作线段 AB ， 使它等于 m+2n（用尺规作图，不写做法，保留作图痕迹）．

17. 计算．
（1）计算：−7×94÷−215．
（2）计算：0−−62÷−43−342．
（3）解方程：4x−520−x=−19．
（4）解方程：x−x−73=x+22+3．

18. 先化简再求值 4xy−34x−12−3xy−23x+1，其中 x=3，y=5．

19. 近日，崂山区教体局对参加 2018 年崂山区禁毒知识竞赛的 2500 名初中学生的初试成绩（成绩均为整数）进行一次抽样调查，所得数据如下表：
成绩分组60.5∼70.570.5∼80.580.5∼90.590.5∼100.5频数50150200100
（1）抽取样本的总人数；
（2）根据表中数据，补全图中频数分布直方图；
（3）若规定初试成绩在 90 分以上（不包括 90 分）的学生进入决赛，则全区进入决赛的初中学生约有多少人．

20. 列方程解应用题
青岛与济南两城市间的高速公路长约 360 千米，现有一长途客车从济南开往青岛，平均速度为 85 千米/时，有一小汽车同时从青岛开往济南，平均速度是 95 千米/时，求两车相遇时各自行驶的路程．

21. 一辆超市配送车从仓库 O 出发，向东走了 4.5 km 到达超市 A，继续走 0.5 km 到达超市 B，然后向西走 9.5 km 到达超市 C，最后回到仓库 O．解答下列问题：
（1）以仓库 O 为原点，以向东为正方向，用 1 个单位长度表示 1 km，在所给的直线上画出数轴，并在数轴上表示出 A，B，C 的位置．
（2）结合数轴计算：超市 C 在超市 A 的什么方向，距超市 A 多远?
（3）若该配送车每千米耗油 0.1 升，在这次送货回仓过程中共耗油多少升?

22. 如图为从三个方向看一个几何体的形状．
（1）任意画出它的一种表面展开图；
（2）若从正面看的长为 10 cm，从上面看正方形的边长为 4 cm，求这个几何体的表面积．

23. 为迎接新年，小红的妈妈在某外贸店为小红购买了一件上衣和一条裤子，已知上衣和裤子标价之和为 600 元，经双方议价，上衣享受九折优惠，裤子享受八折优惠，最终共付款 518 元．
（1）则上衣和裤子的标价各多少元?
（2）在本次交易中，外贸店老板将上衣和裤子在进价的基础上均提高 50% 进行标价，若该老板当天只进行了这一次交易，并且还需要支付店面、水电等其它费用共 100 元，请帮助老板计算当天的收益情况．

24. 如图 1：直线 AB，CD 相交于点 O．
（1）若 ∠AOC=30∘，则 ∠BOC= ∘，∠BOD= ∘；
（2）如图 2，将直线 CD 绕点 O 旋转，请根据下表所给数据将表格补充完整；
∠AOC60∘90∘x∘∠BOD
（3）如图 3，过点 O 分别作 ∠AOC 与 ∠AOD 的角分线 OE，OF，若 ∠BOD 的度数为 α，请用含 α 的代数式表示 ∠COF 的度数．

25. 如图所示，小娟玩游戏：一张纸片，第一次将其撕成四个正方形片，手中共有 4 张纸片，以后每次都将其中一片撕成更小的四个正方形片．如此进行下去，根据上述情况：
（1）当撕 10 次时，小娟手中共有 张纸；
（2）当小娟撕到第 n 次时，手中共有 S 张纸片，请用含 n 的代数式表示 S；
（3）小娟手中能否有 2020 张纸片?如果能，请算出是第几次撕；如果不能，需说明理由．
（4）如果设原正方形的边长为 1，通过不断地分割该面积为 1 的正方形，并把数量关系和几何图形巧妙地结合起来，可以很容易得到一些计算结果，请结合上图计算 3×14+142+143⋯⋯14n．
答案
第一部分
1. B【解析】∵12 的相反数是 −12，
∴ 相反数等于 −12 的是 12．
故选：B．
2. C【解析】A．了解中央电视台《新闻联播》栏目的收视率，适合抽样调查；
B．了解一批洗衣机的使用寿命率，适合抽样调查；
C．了解某班学生对“本学校校训”的知晓率，适合普查；
D．了解渤海中鱼的种类，适合抽样调查；
故选：C．
3. C【解析】根据图形可得，图及图的主视图一样，俯视图不一样，即主视图不变，俯视图改变．
4. C【解析】分数有：0.1234，−512，0.3，19，共 4 个．
故选C．
5. B
【解析】解：∵2x2my3 与 −5xy2n 是同类项，
∴2m=1，2n=3，
解得：m=12，n=32，
∴∣m−n∣=∣12−32∣=1．
故选：B．
6. B【解析】A、 −8+3=−5，故此选项错误；
B、 −12013×1=−1×1=−1，正确；
C、 −52=25，故此选项错误；
D、 −∣−2∣=−2，故此选项错误．
7. B
8. D【解析】设甲乙两地距离为 x 千米，
依题意得：5+2.4x−3≤17，
解得：x≤8．
因此 x 的最大值为 8．
故选：D．
第二部分
9. 长方形
【解析】用一个平面去截一个正方体，如果截去的几何体是一个三棱柱，那么截面的形状一定是长方形．
故答案为：长方形．
10. 3.369×109
【解析】336900 万 =3369000000=3.369×109．
11. 163
【解析】根据题意得：2×5−3m+6=0，
解得：m=163，
故答案为：163．
12. 40
【解析】根据题意得：
20÷10%=200（人），
200−40−20−70−200×15%=40（人）．
答：在这次活动中“最喜欢的职业”为教师的共 40 人．
故答案为：40．
13. 96
14. 120
【解析】由图可得，
图（1）中小正方体的个数为：1，
图（2）中小正方体的个数为：1×2+4×1=6，
图（3）中小正方体的个数为：1×3+4×1+4×2=15，
⋯
则第八个叠放的图形中，小正方体木块总数是：1×8+4×1+4×2+4×3+⋯+4×7=120，
故答案为：120．
第三部分
15. 如图所示：
16. 如图所示：
线段 AB=m+2n．
17. （1） 原式=7×94×521=154 ；
（2） 原式=0−36÷−64−916=916−916=0；
（3） 去括号，得
4x−100+5x=−19.
整理，得
9x=81.
所以
x=9.
（4） 去分母，得
6x−2x−7=3x+2+18.
去括号，得
6x−2x+14=3x+6+18.
移项并合并，得
x=10.
18. 原式=4xy−3x−2−3xy+2x−3=xy−x−5,
当 x=3，y=5 时，
原式=15−3−5=7．
19. （1） 抽取样本的容量 =50+150+200+100=500．
（2） 根据表中数据，补全图中频数分布直方图如图．
（3） 全县进入决赛的学生约为 2500×15=500 人．
20. 设长途客车出发 x 小时时两车相遇，由题意得：
85x+95x=360,
解得：
x=2,
长途客车行驶路程：85×2=170（千米），
小汽车行驶路程：95×2=190（千米）．
答：两车相遇时长途客车行驶路程为 170 千米，小汽车行驶路程 190 千米．
21. （1） 根据题意画出数轴，如图所示：
（2） 根据题意得：超市 C 在超市 A 的西面，距离超市 A:4.5−−4.5=9（千米）；
（3） 根据题意得：5−−4.5×2×0.1=1.9（升），则在这次送货回仓过程中共耗油 1.9 升．
22. （1） 表面展开图如图所示：
（2） 这个几何体的表面积是：4×10×4+4×4×2=192cm2．
23. （1） 设上衣标价 x 元，则裤子标价 600−x 元，由题意得：
0.9x+0.8600−x=518.
解得：
x=380.
裤子标价：600−380=220（元），
答：上衣标价 380 元，则裤子标价 220 元；
（2） 上衣和裤子的进价为：600÷1+50%=400（元），
518−400−100=18（元），
答：当天的收益 18 元．
24. （1） 150；30
【解析】如图 1 中，
∵∠AOC=30∘，
∴∠BOD=∠AOC=30∘，∠BCO=180∘−∠AOC=150∘，
故答案为 150，30．
（2） 60∘；90∘；x∘
【解析】∵∠BOD=∠AOC，
∴ 当 ∠AOC=60∘ 时，∠BOD=60∘，
当 ∠AOC=90∘ 时，∠BOD=90∘，
当 ∠AOC=x∘ 时，∠BOD=x∘，
故答案为 60∘，90∘，x∘．
（3） ∵∠AOC=∠BOD，∠BOD=α，
∴∠AOC=α，
∵OE 平分 ∠AOC，
∴∠EOC=12α，
∵OF 平分 ∠AOD，
∴∠AOF=12∠AOD，∠AOE=12∠AOC，
∴∠EOF=∠AOE+∠AOF=12∠COD=90∘，
∴∠COF=90∘+12α．
25. （1） 31
【解析】由图可得，当撕 10 次时，小娟手中共有：1+3×10=31（张）．
（2） 由图可得，S=1+3n．
（3） 小娟手中能有 2020 张纸片，
令 1+3n=2020，解得 n=673，
即第 673 次撕，正好是 2020 张纸片．
（4） 3×14+142+143⋯⋯14n=34+342+343+⋯+34n=1−14n.