2018-2019学年山东省青岛市平度市八上期末数学试卷

这是一份2018-2019学年山东省青岛市平度市八上期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 2 的平方根是
A. 2B. −2C. ±2D. 4

2. 如图是某动物园的平面示意图，若以大门为原点，向右的方向为 x 轴正方向，向上的方向为 y 轴正方向建立平面直角坐标系，则驼峰所在的象限是
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

3. 如图，把一块含有 45∘ 角的直角三角板的两个顶点放在直尺的对边上．如果 ∠1=20∘，那么 ∠2 的度数是
A. 30∘B. 25∘C. 20∘D. 15∘

4. 下列函数中，y 随 x 的增大而增大的是
A. y=−2x+1B. y=−x−2C. y=x+1D. y=−2x−1

5. 若直角三角形两条直角边长分别为 2，3，则该直角三角形斜边上的高为
A. 13B. 31313C. 61313D. 121313

6. A，B，C，D，E五名同学在一次数学测验中的平均成绩是 80 分，而A，B，C三人的平均成绩是 78 分，下列说法一定正确的是
A. D，E两人的平均成绩是 83 分B. D，E的成绩比其他三人都好
C. 五人成绩的中位数一定是 80 分D. 五人的成绩的众数一定是 80 分

7. 实数 a，b，c 在数轴上的对应点的位置如图所示，则正确的结论是
A. ∣a∣>4B. c−b>0C. ac>0D. a+c>0

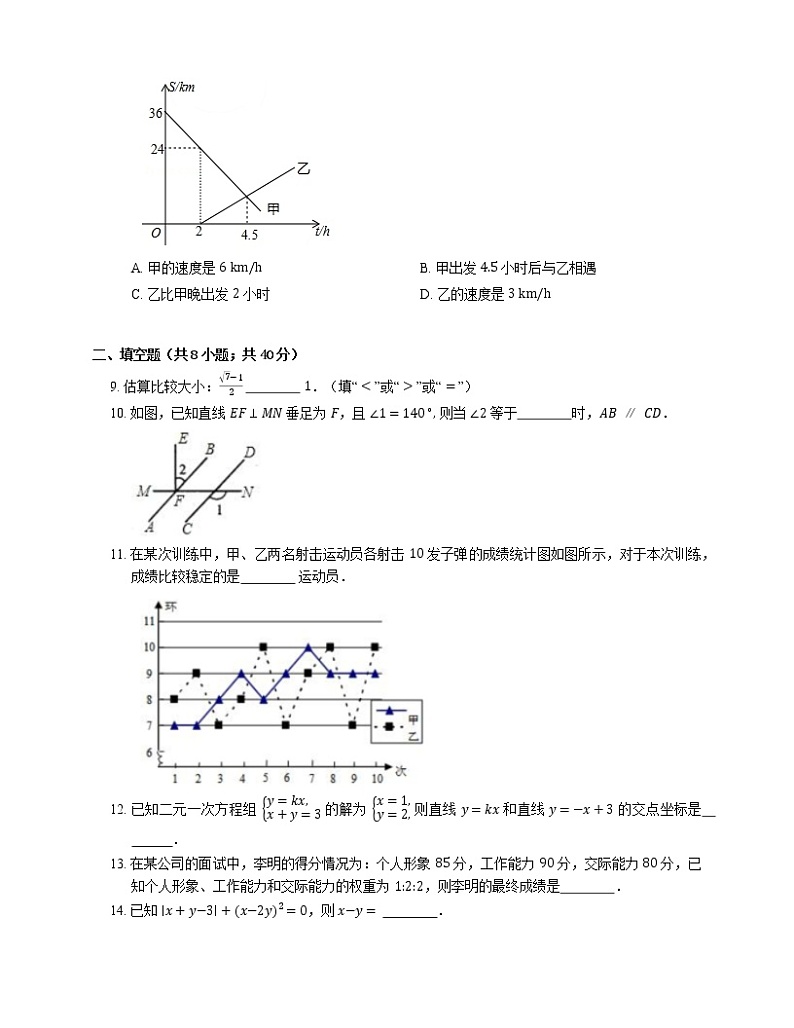
8. 甲、乙两人分别从A，B两地相向而行，他们距B地的距离 skm 与时间 th 的关系如图所示，下列说法错误的是
A. 甲的速度是 6 km/hB. 甲出发 4.5 小时后与乙相遇
C. 乙比甲晚出发 2 小时D. 乙的速度是 3 km/h

二、填空题（共8小题；共40分）
9. 估算比较大小：7−12 1．（填“<”或“>”或“=”）

10. 如图，已知直线 EF⊥MN 垂足为 F，且 ∠1=140∘, 则当 ∠2 等于 时，AB∥CD．

11. 在某次训练中，甲、乙两名射击运动员各射击 10 发子弹的成绩统计图如图所示，对于本次训练，成绩比较稳定的是 运动员．

12. 已知二元一次方程组 y=kx,x+y=3 的解为 x=1,y=2, 则直线 y=kx 和直线 y=−x+3 的交点坐标是 ．

13. 在某公司的面试中，李明的得分情况为：个人形象 85 分，工作能力 90 分，交际能力 80 分，已知个人形象、工作能力和交际能力的权重为 1:2:2，则李明的最终成绩是 ．

14. 已知 ∣x+y−3∣+x−2y2=0，则 x−y= ．

15. 如图，△ABC 中，点 A 的坐标为 0,1，点 C 的坐标为 4,3．如果要使以点 A，B，D 为顶点的三角形与 △ABC 全等，那么点 D 的坐标是 ．

16. 如图，在平面直角坐标系中，△P1OA1，△P2A1A2，△P3A2A3，⋯ 都是等腰直角三角形，其直角顶点 P13,3，P2，P3，⋯ 均在直线 y=−13x+4 上．设 △P1OA1，△P2A1A2，△P3A2A3，⋯ 的面积分别为 S1，S2，S3，⋯，依据图形所反映的规律，S2018= ．

三、解答题（共8小题；共104分）
17. 计算下列各题．
（1）计算：28+23−8．
（2）解方程组：y=x+2,4x+3y=13.
（3）解方程组：x−2y=7,6x+y=3.

18. 已知：如图，FE∥OC，AC 和 BD 相交于点 O，E 是 CD 上一点，F 是 OD 上点，且 ∠1=∠A．
（1）求证：AB∥DC；
（2）若 ∠B=30∘，∠1=65∘，求 ∠OFE 的度数．

19. 某农场去年大豆和小麦的总产量为 200 吨，今年大豆和小麦的总产量为 225 吨，其中大豆比去年增产 5%，小麦比去年增产 15%，求该农场今年大豆和小麦的产量各是多少吨?

20. 如图，已知 ∠1+∠2=180∘，∠3=∠B，试判断 ∠AED 与 ∠ACB 的大小关系，并说明理由．

21. 我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出 5 名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的 5 名选手的决赛成绩如图所示．
平均分分中位数分众数分方差分2初中部a85bs初中2高中部85c100160
（1）根据图示计算出 a，b，c 的值；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好?
（3）计算初中代表队决赛成绩的方差 s初中2，并判断哪一个代表队选手成绩较为稳定．

22. 某批发市场经销龟苓膏粉，其中A品牌的批发价是每包 20 元，B品牌的批发价是每包 25 元，小明计划购买这两种品牌的龟苓膏粉共 1000 包，解答下列问题：
（1）若购买这些龟苓膏粉共花费 22000 元，求两种品牌的龟苓膏粉各购买了多少包?
（2）若凭会员卡在此批发市场购买商品可以获得 8 折优惠，会员卡费用为 500 元，若购买会员卡并用此卡购买这些龟苓膏粉共花费 y 元，设A品牌购买了 x 包，请求出 y 与 x 之间的函数关系式．

23. 材料阅读：如图①所示的图形，像我们常见的学习用品--圆规．我们不妨把这样图形叫做“规形图”．解决问题：
（1）观察“规形图”，试探究 ∠BDC 与 ∠A，∠B，∠C 之间的数量关系，并说明理由；
（2）请你直接利用以上结论，解决以下两个问题：
Ⅰ．如图②，把一块三角尺 DEF 放置在 △ABC 上，使三角尺的两条直角边 DE，DF 恰好经过点 B，C，若 ∠A=40∘，则 ∠ABD+∠ACD= ∘．
Ⅱ．如图③，BD 平分 ∠ABP，CD 平分 ∠ACP，若 ∠A=40∘，∠BPC=130∘，求 ∠BDC 的度数．

24. 如图，一次函数 y=34x+6 的图象与 x，y 轴分别交于 A，B 两点，点 C 与点 A 关于 y 轴对称．动点 P，Q 分别在线段 AC，AB 上（点 P 与点 A，C 不重合），且满足 ∠BPQ=∠BAO．
（1）求点 A，B 的坐标及线段 BC 的长度；
（2）当点 P 在什么位置时，△APQ≌△CBP，说明理由；
（3）当 △PQB 为等腰三角形时，求点 P 的坐标．
答案
第一部分
1. C【解析】∴±22=2，
∴±2=±2．
2. D【解析】如图所示，
熊猫馆、猴山、百草园都在第一象限，横、纵坐标都为正数；
驼峰在第四象限，横坐标为正数，纵坐标为负数，
故选：D．
3. B【解析】根据题意可知，两直线平行，内错角相等，
∴∠1=∠3，
∵∠3+∠2=45∘，
∴∠1+∠2=45∘，
∵∠1=20∘，
∴∠2=25∘．
故选：B．
4. C【解析】A、 ∵ y=−2x+1 中 k=−2<0，∴ y 随 x 的增大而减小，故本选项错误；
B、 ∵ y=−x−2 中 k=−1<0，∴ y 随 x 的增大而减小，故本选项错误；
C、 ∵ y=x+1 中 k=1>0，∴ y 随 x 的增大而增大，故本选项正确；
D、 ∵ y=−2x−1 中 k=−2<0，∴ y 随 x 的增大而减小，故本选项错误．
5. C
【解析】设该直角三角形斜边上的高为 h，
∵ 直角三角形的两条直角边长分别为 2 和 3，
∴ 斜边 =22+33=13，
∵2×3×12=13×h×12，
∴h=61313．
6. A【解析】A、设D，E两人的平均成绩是 83 分，
由题意得，3×78+2x=5×80，
解得 x=83，
所以，D，E两人的平均成绩是 83 分，故本选项正确；
B、无法判断D，E的成绩比其他三人都好，故本选项错误；
C、五人成绩的中位数一定是 80 分，错误，有可能是按成绩排列后中间三位同学的成绩相同，中位数是他们三个人的成绩，故本选项错误；
D、五人的成绩的众数一定是 80 分，错误，有可能没有人正好是 80 分，故本选项错误．
故选：A．
7. B【解析】因为 −4又因为 c>b，所以 c−b>0，所以B正确；
又因为 a<0，c>0，所以 ac<0，所以C不正确；
又因为 a<−3，c<3，所以 a+c<0，所以D不正确；
故选：B．
8. D【解析】如图所示，甲、乙分别从A，B两地相向而行，
从图象中可看出，当 t=0 时，A，B两地距离 s=36km，
甲从A地先出发 2 小时后乙才从B地出发，故选项C正确；
从甲行走的一次函数上看，其速度 v1=36−242=6km/h，A项正确；
从图象中可得到两条直线的交点所对应的时间是甲和乙相遇的时间 4.5h，此时甲已出发 4.5h，故B项正确；
设乙的速度为 v2，则甲乙相遇时他们行走的路程为A，B两地距离可得，
4.5v1+4.5−2v2=36，解得 v2=3.6km/h，故乙的速度为 3.6 km/h，故D项错误．
故选：D．
第二部分
9. <
【解析】∵2<7<3，
∴7−1<2，
∴7−12<1．
10. 50∘
【解析】∵AB∥CD，
∴∠3=∠4（两直线平行，同位角相等）；
又 ∵∠1+∠3=180∘（平角的定义），∠1=140∘（已知），
∴∠3=∠4=40∘，
∵EF⊥MN，
∴∠2+∠4=90∘，
∴∠2=50∘；
故答案为：50∘．
11. 甲
【解析】由图中知，甲的成绩为 7，7，8，9，8，9，10，9，9，9，
乙的成绩为 8，9，7，8，10，7，9，10，7，10，
∴x甲=7+7+8+9+8+9+10+9+9+9÷10=8.5，
x乙=8+9+7+8+10+7+9+10+7+10÷10=8.5，
∴ 甲的方差，
s甲2=2×7−8.52+2×8−8.52+10−8.52+5×9−8.52÷10=0.85,
乙的方差，
s乙2=3×7−8.52+2×8−8.52+2×9−8.52+3×10−8.52÷10=1.45,
∴s甲2 ∴ 甲的射击成绩比乙稳定．
12. 1,2
【解析】联立 y=kx,y=−x+3,
可化为 y=kx,x+y=3,
∴ 方程组的解为 x=1,y=2,
∴ 直线 y=kx 与直线 y=−x+3 的交点坐标为 1,2．
故答案为：1,2．
13. 85 分
【解析】根据题意得：
85×1+90×2+80×21+2+2=85．
14. 1
【解析】∵∣x+y−3∣+x−2y2=0，
∴x+y=3, ⋯⋯①x−2y=0. ⋯⋯②
① − ②，得：3y=3，
解得 y=1，
将 y=1 代入①，得：x+1=3，
解得 x=2，
则 x−y=2−1=1，
故答案为：1．
15. 4,−1 或 −1,3 或 −1,−1
【解析】符合题意的有 3 个，如图，
∵ 点 A，B，C 坐标为 0,1，3,1，4,3，
∴D1 的坐标是 4,−1，D2 的坐标是 −1,3，D3 的坐标是 −1,−1，
故答案为：4,−1 或 −1,3 或 −1,−1．
16. 942017
【解析】如图，分别过点 P1，P2，P3 作 x 轴的垂线段，垂足分别为点 C，D，E，
∵P13,3，且 △P1OA1 是等腰直角三角形，
∴OC=CA1=P1C=3，
设 A1D=a，则 P2D=a，
∴OD=6+a，
∴ 点 P2 坐标为 6+a,a，
将点 P2 坐标代入 y=−13x+4，得：−136+a+4=a，
解得：a=32，
∴A1A2=2a=3，P2D=32，
同理求得 P3E=34，A2A3=32，
∵S1=12×6×3=9，S2=12×3×32=94，S3=12×32×34=916，⋯⋯
∴S2018=942017，
故答案为：942017．
第三部分
17. （1） 原式=42+2−2=52−2=−522.
（2）
y=x+2, ⋯⋯①4x+3y=13. ⋯⋯②①
代入 ②，得：
4x+3x+3=13.
解得：
x=1.
将 x=1 代入 ① 得：
y=1+2=3.
所以方程组的解为 x=1,y=3.
（3）
x−2y=7, ⋯⋯①6x+y=3. ⋯⋯②①+②×2
，得：
13x=13.
解得：
x=1.
将 x=1 代入 ② 得：
6+y=3.
解得：
y=−3.
所以方程组的解为 x=1,y=−3.
18. （1） ∵FE∥OC，
∴∠1=∠C，
∵∠1=∠A，
∴∠A=∠C，
∴AB∥DC．
（2） ∵AB∥DC，
∴∠D=∠B，
∵∠B=30，
∴∠D=30∘，
∵∠OFE 是 △DEF 的外角，
∴∠OFE=∠D+∠1，
∵∠1=65∘，
∴∠OFE=30∘+65∘=95∘．
19. 设农场去年大豆产量为 x 吨，小麦产量为 y 吨，据题意可得：
x+y=200,1+5%x+1+15%y=225,
解方程组，得
x=50,y=150.
即去年大豆产量为 50 吨，实际产量为 50×1+5%=52.5 吨；
去年小麦产量为 150 吨，实际产量为 150×1+15%=172.5 吨；
答：农场今年大豆产量为 52.5 吨，小麦产量为 172.5 吨．
20. ∠AED=∠ACB．
理由：∵∠1+∠4=180∘（平角定义），∠1+∠2=180∘（已知）．
∴∠2=∠4．
∴EF∥AB（内错角相等，两直线平行）．
∴∠3=∠ADE（两直线平行，内错角相等）．
∵∠3=∠B（已知），
∴∠B=∠ADE（等量代换）．
∴DE∥BC（同位角相等，两直线平行）．
∴∠AED=∠ACB（两直线平行，同位角相等）．
21. （1） 初中 5 名选手的平均分 a=75+80+85+85+1005=85，众数 b=85，
高中 5 名选手的成绩是：70，75，80，100，100，故中位数 c=80；
（2） 由表格可知初中部与高中部的平均分相同，初中部的中位数高，故初中部决赛成绩较好；
（3） s初中2=75−852+80−852+85−852+85−852+100−8525=70，
∵s初中2 ∴ 初中代表队选手成绩比较稳定．
22. （1） 设小明需购买A品牌龟苓膏 a 包，B品牌龟苓膏 b 包，
a+b=1000,20a+25b=22000, 得 a=600,b=400,
答：小明需购买A品牌龟苓膏 600 包，B品牌龟苓膏 400 包；
（2） 由题知：y=500+0.8×20x+251000−x=500+0.8×25000−5x=−4x+20500，
答：y 与 x 之间的函数关系是 y=−4x+20500．
23. （1） 如图①，

连接 AD 并延长至点 F，
根据外角的性质，可得：
∠BDF=∠BAD+∠B，
∠CDF=∠C+∠CAD，
又 ∵∠BDC=∠BDF+∠CDF，
∠BAC=∠BAD+∠CAD,
∴∠BDC=∠A+∠B+∠C．
（2） 50
Ⅱ．由（1），可得 ∠BPC=∠BAC+∠ABP+∠ACP，
∠BDC=∠BAC+∠ABD+∠ACD，
∴∠ABP+∠ACP=∠BPC−∠BAC=130∘−40∘=90∘，
又 ∵BD 平分 ∠ABP，CD 平分 ∠ACP，
∴∠ABD+∠ACD=12∠ABP+∠ACP=45∘，
∴∠BDC=45∘+40∘=85∘．
【解析】Ⅰ．由（1）可得，∠BDC=∠ABD+∠ACD+∠A；
又 ∵∠A=40∘，∠D=90∘，
∴∠ABD+∠ACD=90∘−40∘=50∘．
24. （1） 当 x=0 时，y=34x+6=6，
∴ 点 B 的坐标为 0,6；
当 y=0 时，34x+6=0，
解得：x=−8，
∴ 点 A 的坐标为 −8,0；
∵ 点 C 与点 A 关于 y 轴对称，
∴ 点 C 的坐标为 8,0，
∴BC=62+82=10．
（2） 当点 P 的坐标是 2,0 时，△APQ≌△CBP，理由如下：
∵ 点 A 的坐标为 −8,0，点 P 的坐标为 2,0，
∴AP=8+2=10．
∴AP=CB．
∵∠BPQ=∠BAO，∠BAO+∠AQP+∠APQ=180∘，∠APQ+∠BPQ+∠BPC=180∘，
∴∠AQP=∠CPB．
∵A 和 C 关于 y 轴对称，
∴∠PAQ=∠BCP．
在 △APQ 和 △CBP 中，∠AQP=∠CPB,∠PAQ=∠BCP,AP=CB.
∴△APQ≌△CBPAAS．
∴ 当点 P 的坐标是 2,0 时，△APQ≌△CBP．
（3） 分为三种情况：
①当 PB=PQ 时，如图 1 所示，
由（2）知，当点 P 的坐标是 2,0 时，△APQ≌△CBP，
∴PB=PQ，
∴ 此时 P 的坐标是 2,0；
②当 BQ=BP 时，则 ∠BPQ=∠BQP，
∵∠BAO=∠BPQ，
∴∠BAO=∠BQP．
而根据三角形的外角性质得：∠BQP>∠BAO，
∴ 此种情况不存在；
③当 QB=QP 时，则 ∠BPQ=∠QBP=∠BAO，
∴BP=AP，如图 2 所示．
设此时 P 的坐标是 x,0，
在 Rt△OBP 中，由勾股定理得：BP2=OP2+OB2，
∴x+82=x2+62，
解得：x=−74，
∴ 此时 P 的坐标是 −74,0．
综上所述：当 △PQB 为等腰三角形时，点 P 的坐标是 2,0 或 −74,0．