2018-2019学年山东省青岛市市南区八上期末数学试卷

这是一份2018-2019学年山东省青岛市市南区八上期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 以下列数组作为三角形的三条边长，其中能构成直角三角形的是
A. 1，2，3B. 2，3，5C. 1.5，2，2.5D. 13，14，15

2. 下列说法不正确的是
A. 125 的平方根是 ±15B. −9 是 81 的平方根
C. 0.4 的算术平方根是 0.2D. 3−27=−3

3. 某篮球兴趣小组有 15 名同学，在一次投篮比赛中，他们的成绩如条形图所示．这 15 名同学进球数的众数和中位数分别是
A. 10，7B. 7，7C. 9，9D. 9，7

4. 点 Ax1,y1 和 Bx2,y2 都在直线 y=−x−2 上，且 x1≥x2，则 y1 与 y2 的关系是
A. y1≤y2B. y1≥y2C. y1y2

5. 如图，已知 △ABC 在平面直角坐标系中的位置如图所示，将 △ABC 先向下平移 5 个单位，再向左平移 2 个单位，则平移后 C 点的坐标是
A. 5,−2B. 1,−2C. 2,−1D. 2,−2

6. 李明同学早上骑自行车上学，中途因道路施工步行一段路，到学校共用时 15 分钟．他骑自行车的平均速度是 250 米/分钟，步行的平均速度是 80 米/分钟．他家离学校的距离是 2900 米．如果他骑车和步行的时间分别为 x，y 分钟，列出的方程是
A. x+y=14,250x+80y=2900B. x+y=15,80x+250y=2900
C. x+y=14,80x+250y=2900D. x+y=15,250x+80y=2900

7. 如图，△ABC 中，AD 是 BC 边上的高，AE，BF 分别是 ∠BAC，∠ABC 的平分线，∠BAC=50∘，∠ABC=60∘，则 ∠EAD+∠ACD=
A. 75∘B. 80∘C. 85∘D. 90∘

8. 甲骑摩托车从 A 地去 B 地，乙开汽车从 B 地去 A 地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为 s（单位：千米），甲行驶的时间为 t（单位：小时），s 与 t 之间的函数关系如图所示，有下列结论：
①出发 1 小时时，甲、乙在途中相遇；
②出发 1.5 小时时，乙比甲多行驶了 60 千米；
③出发 3 小时时，甲、乙同时到达终点；
④甲的速度是乙速度的一半．
其中，正确结论的个数是
A. 4B. 3C. 2D. 1

二、填空题（共6小题；共30分）
9. 计算：20+455= ．

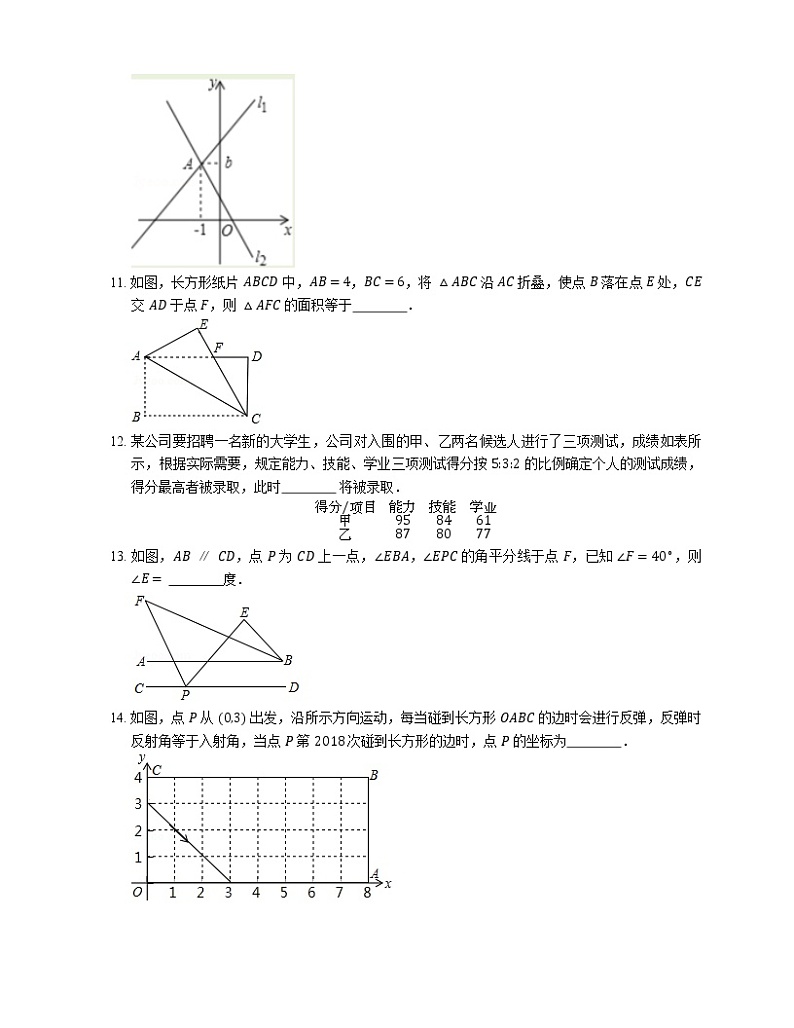
10. 如图，在平面直角坐标系中，直线 l1:y=x+3 与直线 l2:y=mx+1 交于点 A−1,b，则 m= ．

11. 如图，长方形纸片 ABCD 中，AB=4，BC=6，将 △ABC 沿 AC 折叠，使点 B 落在点 E 处，CE 交 AD 于点 F，则 △AFC 的面积等于 ．

12. 某公司要招聘一名新的大学生，公司对入围的甲、乙两名候选人进行了三项测试，成绩如表所示，根据实际需要，规定能力、技能、学业三项测试得分按 5:3:2 的比例确定个人的测试成绩，得分最高者被录取，此时 将被录取．
得分/项目能力技能学业甲958461乙878077

13. 如图，AB∥CD，点 P 为 CD 上一点，∠EBA，∠EPC 的角平分线于点 F，已知 ∠F=40∘，则 ∠E= 度．

14. 如图，点 P 从 0,3 出发，沿所示方向运动，每当碰到长方形 OABC 的边时会进行反弹，反弹时反射角等于入射角，当点 P 第 2018 次碰到长方形的边时，点 P 的坐标为 ．

三、解答题（共10小题；共130分）
15. 在边长为 1 的正方形网格中．
（1）作出 △ABC 关于直线 MN 对称的 △A1B1C1；
（2）若 △A1B1C1 经过图形平移得到 △A2B2C2，当点 A 的坐标是 1,3 时，请建立适当的直角坐标系，分别写出点 A2，B2，C2 的坐标．

16. 计算：
（1）计算：218−32−12；
（2）计算：3+52−2−52+5；
（3）解方程组：3x−12y=1,2x+y=2.

17. “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过 70 千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪 A 的正前方 60 米处的 C 点，过了 5 秒后，测得小汽车所在的 B 点与车速检测仪 A 之间的距离为 100 米．
（1）求 BC 间的距离；
（2）这辆小汽车超速了吗?请说明理由．

18. 为了保护环境，某公交公司决定购买A，B两种型号的全新混合动力公交车共 10 辆，其中A种型号每辆价格为 a 万元，每年节省油量为 2.4 万升；B种型号每辆价格为 b 万元，每年节省油量为 2.2 万升：经调查，购买一辆A型车比购买一辆B型车多 20 万元，购买 2 辆A型车比购买 3 辆B型车少 60 万元．
（1）请求出 a 和 b；
（2）若购买这批混合动力公交车每年能节省 22.4 万升汽油，求购买这批混合动力公交车需要多少万元?

19. 已知：如图，线段 AC 和 BD 相交于点 G，连接 AB，CD，E 是 CD 上一点，F 是 DG 上一点，FE∥CG，且 ∠1=∠A．
（1）求证：AB∥DC；
（2）若 ∠B=30∘，∠1=65∘，求 ∠EFG 的度数．

20. 我市某中学举行“中国梦 ⋅ 校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出 5 名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的 5 名选手的决赛成绩如图所示．
（1）根据图示填写下表；
平均数分中位数分众数分初中部 85 高中部85 100
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．

21. 受天气的影响，某超市鸡蛋供应紧张，需每天从外地调运鸡蛋 1200 斤，超市决定从甲、乙两个大型养殖场调运鸡蛋，已知从甲养殖场每天至少要调出 300 斤，从两养殖场调运鸡蛋到超市的路程和运费如下表：
到超市的路程千米运费元/斤⋅千米甲养殖场2000.012乙养殖场1400.015
（1）设从甲养殖场调运鸡蛋 x 斤，总运费为 W 元，试写出 W 与 x 的函数关系式；
（2）若某天计划从乙养殖场调运 700 斤鸡蛋，则总运费为多少元?
（3）请你帮助超市设计一个调运方案，使得每天调运鸡蛋的总运费最低?

22. 盘锦红海滩景区门票价格 80 元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打 a 折，节假日期间，10 人以下（包括 10 人）不打折，10 人以上超过 10 人的部分打 b 折，设游客为 x 人，门票费用为 y 元，非节假日门票费用 y1（元）及节假日门票费用 y2（元）与游客 x（人）之间的函数关系如图所示．
（1）a= ，b= ；
（2）直接写出 y1，y2 与 x 之间的函数关系式；
（3）导游小王 6 月 10 日（非节假日）带 A 旅游团，6 月 20 日（端午节）带 B 旅游团到红海滩景区旅游，两团共计 50 人，两次共付门票费用 3040 元，求 A，B 两个旅游团各多少人?

23. 在平面直角坐标系 xOy 中有一点，过该点分别作 x 轴和 y 轴的垂线，垂足分别是 A，B，若由该点、原点 O 以及两个垂足所组成的长方形的周长与面积的数值相等，则我们把该点叫做平面直角坐标系中的平衡点．
（1）请判断下列各点中是平面直角坐标系中的平衡点的是 ；（填序号）
① A1,2 ② B−4,4；
（2）若在第一象限中有一个平衡点 N4,m 恰好在一次函数 y=−x+b（b 为常数）的图象上．
①求 m，b 的值；
②一次函数 y=−x+b（b 为常数）与 y 轴交于点 C，问：在这函数图象上，是否存在点 M．使 S△OMC=3S△ONC，若存在，请直接写出点 M 的坐标；若不存在，请说明理由．
（3）经过点 P0,−2，且平行于 x 轴的直线上有平衡点吗?若有，请求出平衡点的坐标；若没有，说明理由．

24. 直线 MN 与直线 PQ 垂直相交于 O，点 A 在直线 PQ 上运动，点 B 在直线 MN 上运动．
（1）如图 1，已知 AE，BE 分别是 ∠BAO 和 ∠ABO 角的平分线，点 A，B 在运动的过程中，∠AEB 的大小是否会发生变化?若发生变化，请说明变化的情况；若不发生变化，试求出 ∠AEB 的大小．
（2）如图 2，已知 AB 不平行 CD，AD，BC 分别是 ∠BAP 和 ∠ABM 的角平分线，又 DE，CE 分别是 ∠ADC 和 ∠BCD 的角平分线，点 A，B 在运动的过程中，∠CED 的大小是否会发生变化?若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图 3，延长 BA 至 G，已知 ∠BAO，∠OAG 的角平分线与 ∠BOQ 的角平分线及延长线相交于 E，F，在 △AEF 中，如果有一个角是另一个角的 3 倍，直接写出 ∠ABO 的度数 = ．
答案
第一部分
1. C【解析】A、 12+22≠32，不能构成直角三角形，故选项不符合题意；
B、 22+32≠52，不能构成直角三角形，故选项不符合题意；
C、 1.52+22=2.52，能构成直角三角形，故选项符合题意；
D、 152+142≠132，不能构成直角三角形，故选项不符合题意．
2. C【解析】0.4 的算术平方根为 105，故C错误．
3. D
4. A【解析】∵ 直线 y=−x−2 的图象 y 随着 x 的增大而减小，
又 ∵x1≥x2，点 Ax1,y1 和 Bx2,y2 都在直线 y=−x−2 上，
∴y1≤y2．
5. B
【解析】∵△ABC 先向下平移 5 个单位，再向左平移 2 个单位，
∴ 平移后点 C 的横坐标为 3−2=1，纵坐标为 3−5=−2，
∴ 点 C 的坐标为 1,−2．
6. D【解析】他骑车和步行的时间分别为 x 分钟，y 分钟，
由题意得：x+y=15,250x+80y=2900.
7. A
8. B【解析】由图象可得：出发 1 小时，甲、乙在途中相遇，故①正确；
甲骑摩托车的速度为 120÷3=40千米/小时，设乙开汽车的速度为 a 千米/小时，则 12040+a=1，解得 a=80，
∴ 乙开汽车的速度为 80 千米/小时，
∴ 甲的速度是乙速度的一半，故④正确；
∴ 出发 1.5 小时，乙比甲多行驶了 1.5×80−40=60（千米），故②正确；
乙到达终点所用的时间为 1.5 小时，甲得到终点所用的时间为 3 小时，故③错误；
∴ 正确的有 3 个．
第二部分
9. 5
【解析】原式=205+455=2+3=5．
10. −1
【解析】由题意知 −1+3=b,−m+1=b,
解得 b=2,m=−1.
故答案为：−1．
11. 263
【解析】∵ 四边形 ABCD 是矩形，
∴AB=CD=4，BC=AD=6，AD∥BC．
∴∠DAC=∠ACB，
∵ 折叠，
∴∠ACB=∠ACE，
∴∠DAC=∠ACE，
∴AF=CF．
在 Rt△CDF 中，CF2=CD2+DF2，
∴AF2=16+6−AF2，
∴AF=133．
∴S△AFC=12×AF×CD=12×133×4=263．
12. 甲
【解析】由题意和图表可得，
甲的平均成绩 =95×5+84×3+61×25+3+2=84.9，
乙的平均成绩 =87×5+80×3+77×25+3+2=82.9，
∵82.9<84.9，
故甲选手得分最高．
13. 80
【解析】设 ∠EPC=2x，∠EBA=2y，
∵∠EBA，∠EPC 的角平分线交于点 F
∴∠CPF=∠EPF=x，∠EBF=∠FBA=y，
∵∠1=∠F+∠ABF=40∘+y，∠2=∠EBA+∠E=2y+∠E，
∵AB∥CD，
∴∠1=∠CPF=x，∠2=∠EPC=2x，
∴∠2=2∠1，
∴2y+∠E=240∘+y，
∴∠E=80∘．
14. 7,4
【解析】如图所示：
经过 6 次反弹后动点回到出发点 0,3，
∵2018÷6=336⋯2，
∴ 当点 P 第 2018 次碰到矩形的边时为第 337 个循环组的第 2 次反弹，
∴ 点 P 的坐标为 7,4．
第三部分
15. （1） 如图所示：△A1B1C1，即为所求．
（2） 点 A28,−5，B24,−3，C27,−3．
16. （1） 原式=62−32−22=522;
（2） 原式=9+65+5−4−5=14+65+1=15+65;
（3）
3x−12y=1, ⋯⋯①2x+y=2, ⋯⋯②
① ×2+ ②得
6x+2x=4,
解得
x=12,
把 x=12 代入②得
1+y=2,
解得
y=1,
所以方程组的解为 x=12,y=1.
17. （1） 在 Rt△ABC 中，
∵AC=60 m，AB=100 m，且 AB 为斜边，
根据勾股定理得：BC=80m；
（2） 这辆小汽车没有超速．
理由：∵80÷5=16m/s，平均速度为：16 m/s，
16 m/s=57.6 km/h，
57.6<70，
∴ 这辆小汽车没有超速．
18. （1） 根据题意得：
a−b=20,3b−2a=60.
解得：
a=120,b=100.
（2） 设A型车购买 x 台，B型车购买 y 台，
根据题意得：
x+y=10,2.4x+2.2y=22.4.
解得：
x=2,y=8.∴120×2+100×8=1040
（万元）．
答：购买这批混合动力公交车需要 1040 万元．
19. （1） ∵FE∥CG，
∴∠1=∠C，
又 ∵∠1=∠A，
∴∠C=∠A，
∴AB∥DC．
（2） ∵AB∥DC，
∴∠D=∠B=30∘，
∵∠1=65∘，
∴∠EFG=∠D+∠1=30∘+65∘=95∘．
20. （1） 85；85；80
【解析】填表：初中平均数为：1575+80+85+85+100=85（分），
众数 85（分）；高中部中位数 80（分）．
（2） 初中部成绩好些．因为两个队的平均数都相同，初中部的中位数高，所以在平均数相同的情况下中位数高的初中部成绩好些．
（3） ∵s12=1575−852+80−852+85−852+85−852+100−852=70，
s22=1570−852+100−852+100−852+75−852+80−852=160．
∴s12因此，初中代表队选手成绩较为稳定．
21. （1） 由题意可得，
W=200×0.012x+1200−x×140×0.015=0.3x+2520,
即 W 与 x 的函数关系式是 W=0.3x+2520．
（2） 当 1200−x=700 时，得 x=500，
当 x=500 时，W=0.3×500+2520=2670．
答：总费用为 2670 元；
（3） ∵W=0.3x+2520，x≥300，
∴ 当 x=300 时，W 取得最小值，
此时 W=2610，1200−x=900．
答：从甲养殖场调运 300 斤，从乙养殖场调运 900 斤，可使得每天调运鸡蛋的总运费最低．
22. （1） 6；8
【解析】由 y1 图象上点 10,480，得到 10 人的费用为 480 元，
∴a=480800×10=6；
由 y2 图象上点 10,800 和 20,1440，得到 20 人中后 10 人费用为 640 元，
∴b=640800×10=8．
（2） y2=80x,0≤x≤1064x+160,x>10．
【解析】设 y1=k1x，
∵ 函数图象经过点 0,0 和 10,480，
∴10k1=480，
∴k1=48，
∴y1=48x；
0≤x≤10 时，设 y2=k2x，
∵ 函数图象经过点 0,0 和 10,800，
∴10k2=800，
∴k2=80，
∴y2=80x，
x>10 时，设 y2=kx+b，
∵ 函数图象经过点 10,800 和 20,1440，
∴10k+b=800,20k+b=1440,
∴k=64,b=160,
∴y2=64x+160；
∴y2=80x,0≤x≤1064x+160,x>10．
（3） 设 B 团有 n 人，则 A 团的人数为 50−n，
当 0≤n≤10 时，80n+48×50−n=3040，解得 n=20（不符合题意舍去），
当 n>10 时，80×10+64×n−10+48×50−n=3040，解得 n=30，
则 50−n=50−30=20．
答：A 团有 20 人，B 团有 30 人．
23. （1） ②
【解析】∵1×2≠1+2×2，
∴ ① A1,2 不是平衡点；
∵4×4=4+4×2，
∴ ② B−4,4 是平衡点．
（2） ① ∵ 点 N4,m 为平衡点，且在第一象限，
∴4m=24+m，
解得：m=4，
∴ 点 N 的坐标为 4,4．
∵ 点 N4,4 在一次函数 y=−x+b（b 为常数）的图象上，
∴4=−4+b，
解得：b=8．
∴m=4，b=8．
②存在，点 M 的坐标为 12,−4 或 −12,20．
【解析】②存在，设点 M 的坐标为 x,−x+8．
∵S△OMC=3S△ONC，即 12OC⋅∣x∣=3×12×4⋅OC，
解得：x=±12，
∴ 点 M 的坐标为 12,−4 或 −12,20．
（3） 没有，理由如下：
设平衡点的坐标为 n,−2，
则 2∣n∣=2+∣n∣×2，
∴2∣n∣=4+2∣n∣，即 0=4．
∵0≠4，
∴ 经过点 P0,−2，且平行于 x 轴的直线上没有平衡点．
24. （1） ∠AEB 的大小不变，
∵ 直线 MN 与直线 PQ 垂直相交于 O，
∴∠AOB=90∘，
∴∠OAB+∠OBA=90∘，
∵AE，BE 分别是 ∠BAO 和 ∠ABO 角的平分线，
∴∠BAE=12∠OAB，∠ABE=12∠ABO，
∴∠BAE+∠ABE=12∠OAB+∠ABO=45∘，
∴∠AEB=135∘．
（2） ∠CED 的大小不变．
延长 AD，BC 交于点 F．
∵ 直线 MN 与直线 PQ 垂直相交于 O，
∴∠AOB=90∘，
∴∠OAB+∠OBA=90∘，
∴∠PAB+∠MBA=270∘，
∵AD，BC 分别是 ∠BAP 和 ∠ABM 的角平分线，
∴∠BAD=12∠BAP，∠ABC=12∠ABM，
∴∠BAD+∠ABC=12∠PAB+∠ABM=135∘，
∴∠F=45∘，
∴∠FDC+∠FCD=135∘，
∴∠CDA+∠DCB=225∘，
∵DE，CE 分别是 ∠ADC 和 ∠BCD 的角平分线，
∴∠CDE+∠DCE=112.5∘，
∴∠E=67.5∘．
（3） 60∘ 或 45∘
【解析】∵∠BAO 与 ∠BOQ 的角平分线相交于 E，
∴∠EAO=12∠BAO，∠EOQ=12∠BOQ，
∴∠E=∠EOQ−∠EAO=12∠BOQ−∠BAO=12∠ABO，
∵AE，AF 分别是 ∠BAO 和 ∠OAG 的角平分线，
∴∠EAF=90∘．
在 △AEF 中，
∵ 有一个角是另一个角的 3 倍，故有：
① ∠EAF=3∠E，∠E=30∘，∠ABO=60∘；
② ∠EAF=3∠F，∠E=60∘，∠ABO=120∘；
③ ∠F=3∠E，∠E=22.5∘，∠ABO=45∘；
④ ∠E=3∠F，∠E=67.5∘，∠ABO=135∘．
∴∠ABO 为 60∘ 或 45∘．