2018_2019学年无锡市梁溪区七上期末数学试卷

这是一份2018_2019学年无锡市梁溪区七上期末数学试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. −2018 的相反数是
A. 2018B. −2018C. ±2018D. −12018

2. 下列各式计算正确的是
A. 5a＋a＝5a2B. 5a＋b＝5ab
C. 5a2b−3ab2＝2a2bD. 2ab2−5b2a＝−3ab2

3. 数轴上三个点表示的数分别为 p，r，s．若 p−r=5，s−p=2，则 s−r 等于
A. 3B. −3C. 7D. −7

4. 如图，直线 AB，CD 相交于点 O，OD 平分 ∠BOE，则 ∠AOD 的补角的个数为
A. 1 个B. 2 个C. 3 个D. 4 个

5. 若 x−12+2y+12=0，则 x2+y2 的值是
A. 38B. 12C. −18D. −38

6. 点 M，N，P 和原点在数轴上的位置如图所示，有理数 a，b，c 各自对应着 M，N，P 三个点中的某一点，且 ab0，ac>bc，那么表示数 b 的点为
A. 点 MB. 点 NC. 点 PD. 无法确定

7. 某道路一侧原有路灯 106 盏，相邻两盏灯的距离为 36 米，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为 70 米，则需更换的新型节能灯有
A. 54 盏B. 55 盏C. 56 盏D. 57 盏

8. 在同一平面内，下列说法中正确的是
A. 过一点有无数条直线与已知直线垂直
B. 一条直线的平行线有且只有一条
C. 若直线 a∥b，a⊥c，则 b⊥c
D. 若两条线段不相交，则它们互相平行

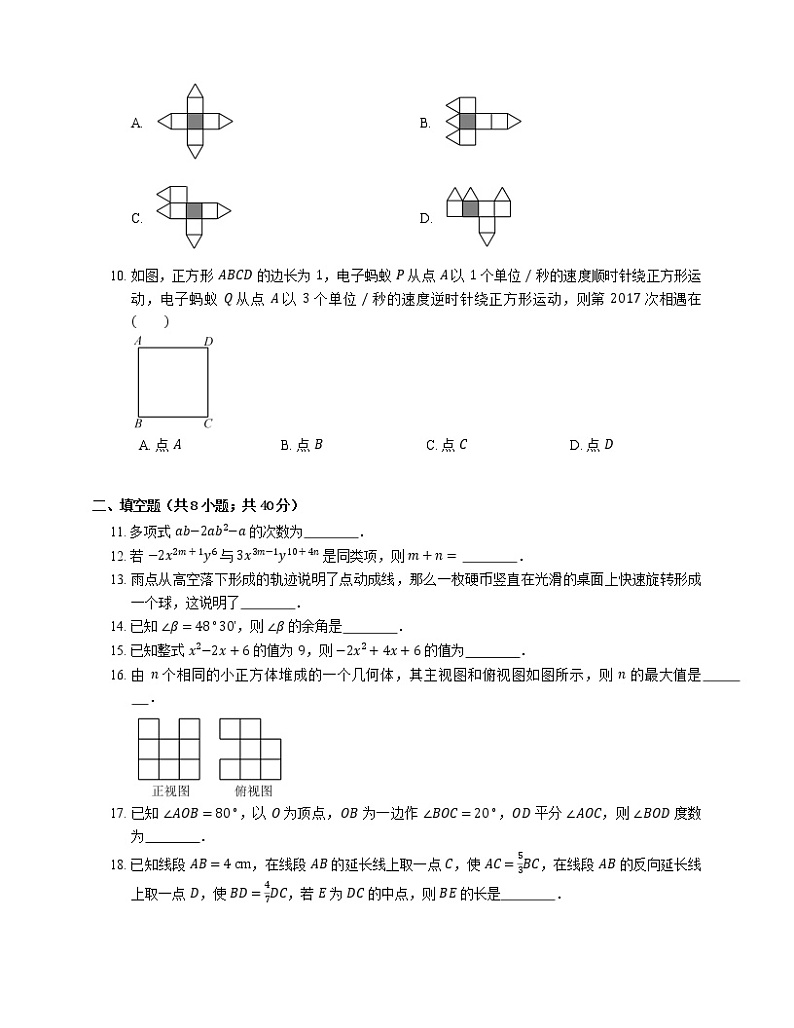
9. 如图，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色．下列图形中，是该几何体的表面展开图的是
A. B.
C. D.

10. 如图，正方形 ABCD 的边长为 1，电子蚂蚁 P 从点 A 以 1 个单位 / 秒的速度顺时针绕正方形运动，电子蚂蚁 Q 从点 A 以 3 个单位 / 秒的速度逆时针绕正方形运动，则第 2017 次相遇在
A. 点 AB. 点 BC. 点 CD. 点 D

二、填空题（共8小题；共40分）
11. 多项式 ab−2ab2−a 的次数为 ．

12. 若 −2x2m+1y6 与 3x3m−1y10+4n 是同类项，则 m+n= ．

13. 雨点从高空落下形成的轨迹说明了点动成线，那么一枚硬币竖直在光滑的桌面上快速旋转形成一个球，这说明了 ．

14. 已知 ∠β=48∘30ʹ，则 ∠β 的余角是 ．

15. 已知整式 x2−2x+6 的值为 9，则 −2x2+4x+6 的值为 ．

16. 由 n 个相同的小正方体堆成的一个几何体，其主视图和俯视图如图所示，则 n 的最大值是 ．

17. 已知 ∠AOB=80∘，以 O 为顶点，OB 为一边作 ∠BOC=20∘，OD 平分 ∠AOC，则 ∠BOD 度数为 ．

18. 已知线段 AB=4 cm，在线段 AB 的延长线上取一点 C，使 AC=53BC，在线段 AB 的反向延长线上取一点 D，使 BD=47DC，若 E 为 DC 的中点，则 BE 的长是 ．

三、解答题（共8小题；共104分）
19. 计算：
（1）12+56−712×−24；
（2）−14−7÷2−−32．

20. 解下列方程．
（1）2x−1+1=0；
（2）2x−12=1−3−x4．

21. （1）先化简再求值：3x2y−2x2y−32xy−x2y+6xy，其中 x=−12，y=2．
（2）已知 y=1 是关于 y 的方程 2−13m−y=2y 的解，求关于 x 的方程 mx−3−2=m2x−8 的解．

22. 如图，所有小正方形的边长都为 1，A，B，C 都在格点上（小正方形的顶点叫做格点）．请仅用没有刻度的直尺完成画图（不要求写画法）及解答：
（1）过点 C 画直线 AB 的平行线 CD；
（2）过点 A 画直线 BC 的垂线，并注明垂足为 G；过点 A 画直线 AB 的垂线，交 BC 于点 H；
（3）线段 的长度是点 A 到直线 BC 的距离；
（4）∠B 与 ∠HAG 的大小关系为 ，理由是 ．

23. 如图所示是长方体纸盒的平面展开图，设 AB=x cm，若 AD=4x cm，AN=3x cm．
（1）求长方形 DEFG 的周长与长方形 ABMN 的周长（用字母 x 进行表示）；
（2）若长方形 DEFG 的周长比长方形 ABMN 的周长少 8 cm，求 x 的值；
（3）在第（2）问的条件下，求原长方体纸盒的容积．

24. 已知直线上有 A，B 两点，AB=24．动点 P 从点 A 出发，以每秒 3 个单位长度的速度沿直线向左匀速运动；同时动点 Q 从点 B 出发，以每秒 2 个单位长度的速度沿直线向右匀速运动，设点 P 运动时间为 t（t>0，单位 s）．当 A，P，Q 三个点中恰有一点到另外两点的距离相等时，求 t 的值．

25. 某商场经销的甲、乙两种商品，甲种商品每件售价 60 元，利润率为 50%；乙种商品每件进价 50 元，售价 80 元．（利润率=售价−进价进价×100%）
（1）甲种商品每件进价为 元，每件乙种商品利润率为 ．
（2）若该商场同时购进甲、乙两种商品共 500 件，总进价为 21000 元，求购进甲种商品多少件?
（3）在元旦期间，该商场对乙种商品进行如下的优惠促销活动：
打折前一次性购物总金额优惠措施不超过450元不优惠超过450元,但不超过600元按售价打9折超过600元其中600元部分8.2折优惠,超过600元的部分打3折优惠
按上述优惠条件，若小华一次性购买乙种商品实际付款 504 元，求小华在该商场购买乙种商品多少件?

26. 如图 1，射线 OC 在 ∠AOB 的内部，图中共有 3 个角：∠AOB，∠AOC 和 ∠BOC，若其中有一个角的度数是另一个角的度数的两倍，则称射线 OC 是 ∠AOB 的“奇妙线”．
（1）一个角的平分线 这个角的“奇妙线”．（填“是”或“不是”）
（2）如图 2，若 ∠MPN=60∘，射线 PQ 绕点 P 从 PN 位置开始，以每秒 10∘ 的速度逆时针旋转，当 ∠QPN 首次等于 180∘ 时停止旋转，设旋转的时间为 ts．
①当 t 为何值时，射线 PM 是 ∠QPN 的“奇妙线”?
②若射线 PM 同时绕点 P 以每秒 6∘ 的速度逆时针旋转，并与 PQ 同时停止旋转．请求出当射线 PQ 是 ∠MPN 的“奇妙线”时 t 的值．
答案
第一部分
1. A
2. D
3. C
4. C
5. B
6. A
7. B
8. C
9. B
10. D
第二部分
11. 3
12. 1
【解析】∵−2x2m+1y6 与 3x3m−1y10+4n 是同类项，
∴2m+1=3m−1，10+4n=6，
∴n=−1，m=2，
∴m+n=2−1=1．
13. 面动成体
14. 41∘30ʹ
15. 0
16. 18
17. 30∘ 或 50∘
18. 1
第三部分
19. （1） 原式=−12−20+14=−18.
（2） 原式=−1−7÷2−9=−1+1=0.
20. （1）
2x−2+1=0.2x=1.x=12.
（2）
22x−1=4−3−x.4x−2=4−3+x.x=1.
21. （1） 原式=3x2y−2x2y−6xy+3x2y+6xy=3x2y−2x2y+6xy−3x2y−6xy=−2x2y.
当 x=−12，y=2 时，
上式=−2×−122×2=−1.
（2） 把 y=1 代入方程得：2−13m−1=2，解得：m=1．
把 m=1 代入所求方程得：x−3−2=2x−8，得：x=3．
22. （1） 如图所示，直线 CD 即为所求作的直线 AB 的平行线；
（2） 如图所示（端点处可以出头）；
（3） AG
（4） 相等；同角的余角相等
23. （1） ∵AB=x cm，AD=4x cm，AN=3x cm，
∴ 长方形 DEFG 的周长为 2x+2x=6x cm，
长方形 ABMN 的周长为 2x+3x=8x cm．
（2） 依题意，8x−6x=8，解得：x=4．
（3） 原长方体的容积为 x⋅2x⋅3x=6x3，
将 x=4 代入，可得容积 6x3=384 cm2．
24. 当 P 是 QA 的中点时，24−2t=23t，解得 t=3；
当 P，Q 重合时，24−2t=3t，解得 t=245；
当 Q 是 PA 的中点时，3t=224−2t，解得 t=487；
当 Q，A 重合时，2t=24，解得 t=12；
当 t>12 时，AQ=2t−24，AP=3t，显然 AQ≠AP．
综上，t 的值为 3 或 245 或 487 或 12．
25. （1） 40；60%
（2） 设甲种商品购进 x 件，则乙种商品购进 500−x 件，根据题意得：
40x+50500−x=21000.
解得：
x=400.
答：故购进甲种商品 400 件．
（3） 设小华购买了乙种商品 y 件，
∵504>450，
∴ 小华享受了优惠价．
当 450600 时，600×0.82+80y−600×0.3=504，解得 y=8；
答：小华在该商场购买乙种商品 7 件或 8 件．
26. （1） 是
（2） ①由题意可知：共有三种情况，
当第一次满足时，10t=60+12×60，解得：t=9；
当第二次满足时，10t=2×60，解得：t=12；
当第三次满足时，10t=60+2×60，解得：t=18．
综上所述，当 t 的值为 9 或 12 或 18 时，PM 是 ∠QPN 的“奇妙线”．
②由题意可知：
10t=136t+60 时，解得：t=52；
10t=126t+60 时，解得：t=207；
10t=236t+60 时，解得：t=203．
综上所述：当射线 PQ 是 ∠MPN 的“奇妙线”时，t 的值为 307 或 52 或 203．