2020-2021学年广东省肇庆市封开县八年级（下）期末数学试卷

这是一份2020-2021学年广东省肇庆市封开县八年级（下）期末数学试卷，共22页。试卷主要包含了解答题等内容，欢迎下载使用。

1．（3分）下列根式中是最简二次根式的是（ ）
A．B．C．D．
2．（3分）若在实数范围内有意义，则x的取值范围是（ ）
A．x＜B．x＜2C．x≥D．x≤
3．（3分）满足下列条件的△ABC中，不是直角三角形的是（ ）
A．∠A：∠B：∠C＝2：4：6B．AC＝，BC＝，AB＝
C．AC＝6，BC＝8，AB＝10D．AC＝1，BC＝2，AB＝
4．（3分）在平行四边形ABCD中，∠B+∠D＝100°，则∠A等于（ ）
A．50°B．130°C．100°D．65°
5．（3分）直线y＝3x+2与y轴的交点坐标为（ ）
A．（0，3）B．（﹣，0）C．（0，2）D．（0，﹣2）
6．（3分）若+|2a﹣b+1|＝0，则（b﹣a）2021＝（ ）
A．﹣1B．1C．52021D．﹣52021
7．（3分）如图，在Rt△ABC中，∠C＝90°，AC＜BC，分别以顶点A、B为圆心，大于AB的长为半径作圆弧，两条圆弧交于点M、N作直线MN交边CB于点D．若AD＝5，CD＝3，则AB的长是（ ）
A．10B．8C．12D．4
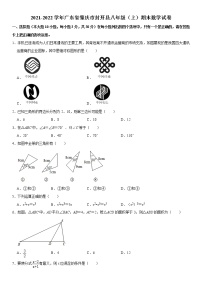
8．（3分）如图，在△ABC中，D，E分别是AB，AC的中点，AC＝10，F是DE上一点，连接AF，CF，DF＝1．若∠AFC＝90°，则BC的长度为（ ）
A．10B．12C．14D．16
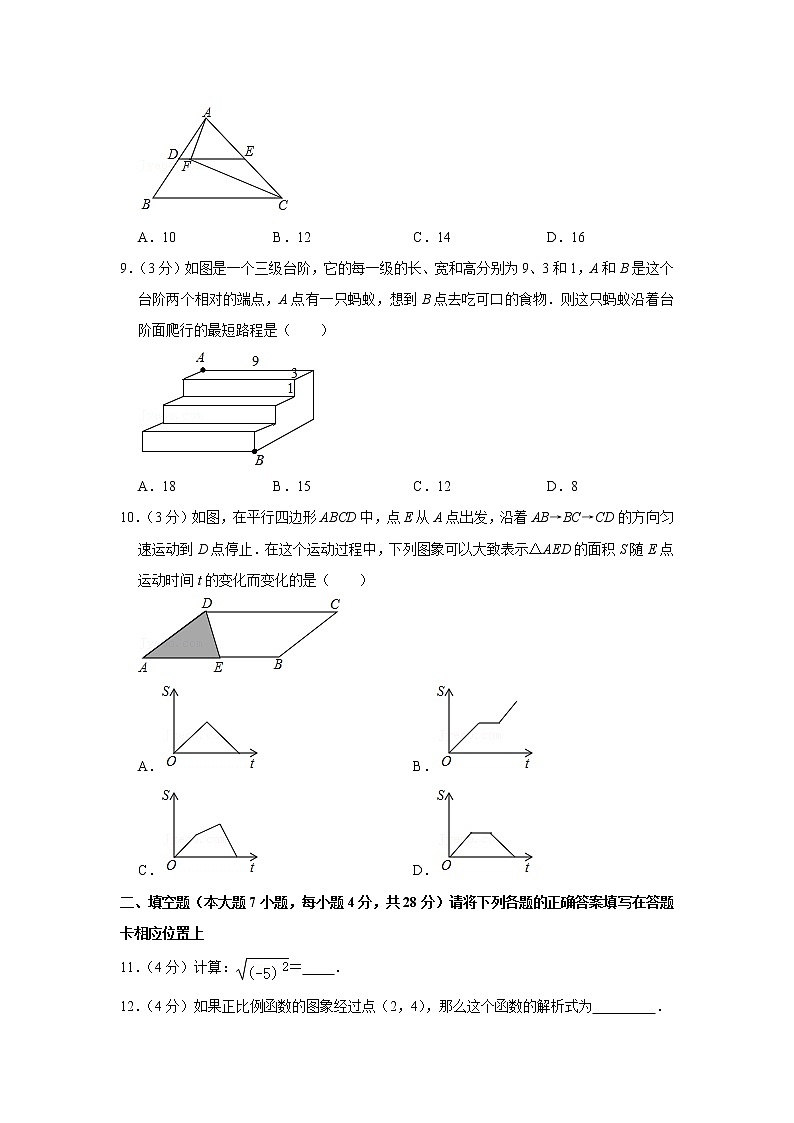
9．（3分）如图是一个三级台阶，它的每一级的长、宽和高分别为9、3和1，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物．则这只蚂蚁沿着台阶面爬行的最短路程是（ ）
A．18B．15C．12D．8
10．（3分）如图，在平行四边形ABCD中，点E从A点出发，沿着AB→BC→CD的方向匀速运动到D点停止．在这个运动过程中，下列图象可以大致表示△AED的面积S随E点运动时间t的变化而变化的是（ ）
A．B．
C．D．
二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应位置上
11．（4分）计算：＝ ．
12．（4分）如果正比例函数的图象经过点（2，4），那么这个函数的解析式为 ．
13．（4分）如图是马口生态公园的一角，有人为了抄近道而避开横平竖直的路的拐角∠ABC，而走“捷径AC”，于是在草坪内走出了一条不该有的“路AC”．已知AB＝40米，BC＝30米，他们踩坏草坪，只为少走 米的路．
14．（4分）已知最简二次根式与可以合并，则a+b的值为 ．
15．（4分）点P（a，b）在函数y＝﹣3x+2的图象上，则代数式9a+3b﹣1的值等于 ．
16．（4分）在弹性限度内，弹簧的长度y（cm）是所挂物体质量x（kg）的一次函数．一根弹簧不挂物体时长15cm；当所挂物体的质量为5kg时，弹簧长20cm．所挂物体质量为8kg时弹簧的长度是 cm．
17．（4分）如图，正方形ABCD中，AD＝4+2，已知点E是边AB上的一动点（不与A、B重合）将△ADE沿DE对折，点A的对应点为P，当PA＝PB时，则线段AE＝ ．
三、解答题（）（3本大题3小题，每小题6分，共18分）
18．（6分）计算：．
19．（6分）如图，在四边形ABCD中，AD∥BC，∠B＝∠C．E是边BC上一点，且DE＝DC．求证：AD＝BE．
20．（6分）如图，台风过后，某市体育中心附近一棵大树在高于地面3米处折断，大树顶部落在距离大树底部4米处的地面上．求这棵树折断之前的高度．
四、解答题（二）（本大题3小题，每小题8分，共24分）
21．（8分）在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数（单位：元），并绘制成如图所示的统计图．
（1）本次调查的人数是 ；
（2）这组数据的众数为 元，中位数为 元；
（3）求这组数据的平均数．
22．（8分）某快递公司每天上午9：00～10：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，y（件）与时间x（分）之间的函数图象如图所示，
（1）求出甲仓库揽收快件y（件）与时间x（分）之间的函数解析式；
（2）若已知乙仓库用来派发快件y（件）与时间x（分）之间的函数解析式是y＝﹣4x+240（0＜x＜60），问经过多少分钟时，两仓库快递件数相同，都是多少件？
23．（8分）为了响应“足球进学校”的号召，某学校准备到体育用品批发市场购买A型号与B型号两种足球，其中A型号足球的批发价是每个200元，B型号足球的批发价是每个250元，该校需购买A，B两种型号足球共100个．
（1）若该校购买A，B两种型号足球共用了22000元，则分别购买两种型号足球多少个？
（2）若该校计划购进A型号足球的数量不多于B型号足球数量的9倍，请求出最省钱的购买方案，并说明理由．
五、解答题（三）（本大题2小题，每小题10分，共20分）
24．（10分）如图，直线y＝x﹣2与x轴y轴分别交于A、B两点在y轴上有一点C（0，4），D是OA上一点．
（1）点A的坐标： ；点B的坐标 ；
（2）若△COD≌△AOB，求直线CD的表达式；
（3）在（2）的条件下，x轴上是否存在点P，使得△PCD是等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
25．（10分）如图，在四边形ABCD中，AB＝AD，∠DAB＝90°，AC平分∠DAB，作DE∥BC交AC于点E，连接BE．
（1）求证：△ADE≌△ABE；
（2）求证：四边形DEBC是菱形；
（3）若∠CDE＝2∠EDA，CE＝2，求AD的长．
2020-2021学年广东省肇庆市封开县八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请在答题卡上把正确的选项涂黑.
1．（3分）下列根式中是最简二次根式的是（ ）
A．B．C．D．
【分析】直接根据最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式判断即可．
【解答】解：A、是最简二次根式，符合题意；
B、＝2，不是最简二次根式，不符合题意；
C、＝2，不是最简二次根式，不符合题意；
D、＝，不是最简二次根式，不符合题意；
故选：A．
2．（3分）若在实数范围内有意义，则x的取值范围是（ ）
A．x＜B．x＜2C．x≥D．x≤
【分析】根据被开方数大于等于0列式计算即可得解．
【解答】解：由题意得，1﹣2x≥0，
解得x≤．
故选：D．
3．（3分）满足下列条件的△ABC中，不是直角三角形的是（ ）
A．∠A：∠B：∠C＝2：4：6B．AC＝，BC＝，AB＝
C．AC＝6，BC＝8，AB＝10D．AC＝1，BC＝2，AB＝
【分析】依据勾股定理的逆定理，三角形内角和定理以及直角三角形的定义，即可得到结论．
【解答】解：A．∵∠A：∠B：∠C＝2：4：6，
∴∠C＝×180°＝90°，
∴△ABC是直角三角形，故A选项不符合题意；
B．∵BC2+AC2＝4+3＝7，AB2＝（）2＝5，
∴BC2+AC2≠AB2，
∴△ABC不是直角三角形，故B选项符合题意；
C．∵62+82＝36+64＝100＝102，
∴AC2+BC2＝AB2，
∴△ABC是直角三角形，故C选项不符合题意；
D．∵12+22＝1+4＝5＝（）2，
∴AC2+BC2＝AB2，
∴△ABC是直角三角形，故D选项不符合题意．
故选：B．
4．（3分）在平行四边形ABCD中，∠B+∠D＝100°，则∠A等于（ ）
A．50°B．130°C．100°D．65°
【分析】由平行四边形的性质可得∠B＝∠D，∠A+∠B＝180°，即可求解．
【解答】解：∵四边形ABCD是平行四边形，
∴∠B＝∠D，∠A+∠B＝180°，
∵∠B+∠D＝100°，
∴∠B＝∠D＝50°，
∴∠A＝130°，
故选：B．
5．（3分）直线y＝3x+2与y轴的交点坐标为（ ）
A．（0，3）B．（﹣，0）C．（0，2）D．（0，﹣2）
【分析】先令x＝0求出y的值即可求出直线y＝3x+2与y轴交点的坐标．
【解答】解：∵令x＝0，则y＝2，
∴直线y＝3x+2与y轴交点的坐标是（0，2）．
故选：C．
6．（3分）若+|2a﹣b+1|＝0，则（b﹣a）2021＝（ ）
A．﹣1B．1C．52021D．﹣52021
【分析】直接利用非负数的性质得出a，b的值，再利用有理数的乘方运算法则计算得出答案．
【解答】解：∵+|2a﹣b+1|＝0，
∴a+2＝0，2a﹣b+1＝0，
解得：a＝﹣2，b＝﹣3，
∴（b﹣a）2021＝[﹣3﹣（﹣2）]2021＝（﹣1）2021＝﹣1．
故选：A．
7．（3分）如图，在Rt△ABC中，∠C＝90°，AC＜BC，分别以顶点A、B为圆心，大于AB的长为半径作圆弧，两条圆弧交于点M、N作直线MN交边CB于点D．若AD＝5，CD＝3，则AB的长是（ ）
A．10B．8C．12D．4
【分析】利用勾股定理求出AC，再利用线段的垂直平分线的性质求出DB，再利用勾股定理求出AB即可．
【解答】解：∵∠C＝90°，AD＝5，CD＝3，
∴AC＝＝＝4，
由作图可知，MN垂直平分线段AB，
∴DA＝DB＝5，
∴BC＝CD+DB＝3+5＝8，
∴AB＝＝＝4．
故选：D．
8．（3分）如图，在△ABC中，D，E分别是AB，AC的中点，AC＝10，F是DE上一点，连接AF，CF，DF＝1．若∠AFC＝90°，则BC的长度为（ ）
A．10B．12C．14D．16
【分析】先证明EF＝5，继而得到DE＝6；再证明DE为△ABC的中位线，即可解决问题．
【解答】解：如图，∵∠AFC＝90°，E是AC的中点，
∴Rt△ACF中，EF＝AC＝＝5，
∴DE＝1+5＝6；
∵D，E分别是AB，AC的中点，
∴DE为△ABC的中位线，
∴BC＝2DE＝12，
故选：B．
9．（3分）如图是一个三级台阶，它的每一级的长、宽和高分别为9、3和1，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物．则这只蚂蚁沿着台阶面爬行的最短路程是（ ）
A．18B．15C．12D．8
【分析】此类题目只需要将其展开便可直观的得出解题思路．将台阶展开得到的是一个矩形，蚂蚁要从B点到A点的最短距离，便是矩形的对角线，利用勾股定理即可解出答案．
【解答】解：将台阶展开，如图，
因为AC＝3×3+1×3＝12，BC＝9，
所以AB2＝AC2+BC2＝225，
所以AB＝15，
所以蚂蚁爬行的最短线路为15．
故选：B．
10．（3分）如图，在平行四边形ABCD中，点E从A点出发，沿着AB→BC→CD的方向匀速运动到D点停止．在这个运动过程中，下列图象可以大致表示△AED的面积S随E点运动时间t的变化而变化的是（ ）
A．B．
C．D．
【分析】分点E在边AB上、点E在边BC上及点E在边CD上三种情况考虑：当点E在边AB上时，由高不变底逐渐增大可得出面积S逐渐增大；当点E在边BC上时，由底和高都不变可得出面积S为定值；当点E在边CD上时，由高不变底逐渐减小可得出面积S逐渐减小．再对照四个选项中的函数图象即可得出结论．
【解答】解：当点E在边AB上时，高不变，底逐渐增大，
∴面积S逐渐增大；
当点E在边BC上时，底和高都不变，
∴面积S为定值；
当点E在边CD上时，高不变，底逐渐减小，
∴面积S逐渐减小．
故选：D．
二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应位置上
11．（4分）计算：＝ 5 ．
【分析】根据二次根式的基本性质进行解答即可．
【解答】解：原式＝＝5．
故答案为：5．
12．（4分）如果正比例函数的图象经过点（2，4），那么这个函数的解析式为 y＝2x ．
【分析】将点（2，4）直接代入即可求得函数的解析式．
【解答】解：设函数的解析式是y＝kx（k≠0），
把（2，4）代入就得到：2k＝4，
解得：k＝2，
因而这个函数的解析式为：y＝2x．
13．（4分）如图是马口生态公园的一角，有人为了抄近道而避开横平竖直的路的拐角∠ABC，而走“捷径AC”，于是在草坪内走出了一条不该有的“路AC”．已知AB＝40米，BC＝30米，他们踩坏草坪，只为少走 20 米的路．
【分析】先判断△ABC为直角三角形，然后根据勾股定理求出AC即可
【解答】解：在Rt△ABC中，∵AB＝40米，BC＝30米，
∴AC＝＝50，30+40﹣50＝20，
∴他们踩坏了50米的草坪，只为少走20米的路．
故答案为：20．
14．（4分）已知最简二次根式与可以合并，则a+b的值为 2 ．
【分析】根据同类二次根式的概念列出方程组，解方程组求出a、b，计算即可．
【解答】解：由题意得，，
解得，，
则a+b＝1+1＝2，
故答案为：2．
15．（4分）点P（a，b）在函数y＝﹣3x+2的图象上，则代数式9a+3b﹣1的值等于 5 ．
【分析】将P（a，b）代入y＝﹣3x+2可得3a+b的值，从而可得答案．
【解答】解：将P（a，b）代入y＝﹣3x+2得b＝﹣3a+2，
∴3a+b＝2，
∴9a+3b﹣1＝3（3a+b）﹣1＝3×2﹣1＝5，
故答案为：5．
16．（4分）在弹性限度内，弹簧的长度y（cm）是所挂物体质量x（kg）的一次函数．一根弹簧不挂物体时长15cm；当所挂物体的质量为5kg时，弹簧长20cm．所挂物体质量为8kg时弹簧的长度是 23 cm．
【分析】根据题意可以求得y与x的函数关系式，从而可以求得当x＝8时对应的y值，本题得以解决．
【解答】解：设y与x的函数关系式为y＝kx+15，
∵x＝5时，y＝20，
∴20＝5k+15，得k＝1，
∴y＝x+15，
当x＝8时，y＝8+15＝23，
故答案为：23．
17．（4分）如图，正方形ABCD中，AD＝4+2，已知点E是边AB上的一动点（不与A、B重合）将△ADE沿DE对折，点A的对应点为P，当PA＝PB时，则线段AE＝ 2 ．
【分析】过点P作MN⊥AB于N，交CD于M，可证四边形ADMN是矩形，可得MN＝AD＝4+2，由折叠的性质可得AD＝DP＝4+2，AE＝PE，由勾股定理可求MP，AE的长．
【解答】解：如图，过点P作MN⊥AB于N，交CD于M，
∵四边形ABCD是正方形，
∴AB＝CD＝AD＝4+2，CD∥AB，
∵MN⊥AB，
∴MN⊥CD，
∴四边形ADMN是矩形，
∴MN＝AD＝4+2，
由折叠可知：AD＝DP＝4+2，AE＝PE，
∵PA＝PB，
∴MN是AB的垂直平分线，
∴DM＝CM＝2+，AN＝NB＝2+，
∴MP＝＝＝2+3，
∴PN＝1，
∵PE2＝PN2+EN2，
∴AE2＝1+（2+﹣AE）2，
∴AE＝2，
故答案为2．
三、解答题（）（3本大题3小题，每小题6分，共18分）
18．（6分）计算：．
【分析】直接利用平方差公式化简，进而计算得出答案．
【解答】解：原式＝（）2﹣（）2+2
＝3﹣5+2
＝0．
19．（6分）如图，在四边形ABCD中，AD∥BC，∠B＝∠C．E是边BC上一点，且DE＝DC．求证：AD＝BE．
【分析】根据等边对等角的性质求出∠DEC＝∠C，再由∠B＝∠C得∠DEC＝∠B，所以AB∥DE，得出四边形ABED是平行四边形，进而得出结论．
【解答】证明：∵DE＝DC，
∴∠DEC＝∠C．
∵∠B＝∠C，
∴∠B＝∠DEC，
∴AB∥DE，
∵AD∥BC，
∴四边形ABED是平行四边形．
∴AD＝BE．
20．（6分）如图，台风过后，某市体育中心附近一棵大树在高于地面3米处折断，大树顶部落在距离大树底部4米处的地面上．求这棵树折断之前的高度．
【分析】画出图形，由勾股定理求出AB的长，即可求解．
【解答】解：如图，由题意得：∠ACB＝90°，AC＝3米，BC＝4米，
由勾股定理得：AB＝＝＝5（米），
∴AC+AB＝3+5＝8（米），
即这棵树折断之前的高度为8米．
四、解答题（二）（本大题3小题，每小题8分，共24分）
21．（8分）在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数（单位：元），并绘制成如图所示的统计图．
（1）本次调查的人数是 30 ；
（2）这组数据的众数为 10 元，中位数为 10 元；
（3）求这组数据的平均数．
【分析】（1）由题意得出本次调查的人数是6+11+8+5＝30；
（2）由众数和中位数的定义即可得出结果；
（3）由加权平均数公式即可得出结果．
【解答】解：（1）本次调查的人数是6+11+8+5＝30；
（2）这组数据的众数为10元，中位数为10元；
（2）＝×（5×6+10×11+15×8+20×5）＝12（元）．
故答案为：30，10，10．
22．（8分）某快递公司每天上午9：00～10：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，y（件）与时间x（分）之间的函数图象如图所示，
（1）求出甲仓库揽收快件y（件）与时间x（分）之间的函数解析式；
（2）若已知乙仓库用来派发快件y（件）与时间x（分）之间的函数解析式是y＝﹣4x+240（0＜x＜60），问经过多少分钟时，两仓库快递件数相同，都是多少件？
【分析】（1）设甲仓库揽收快件y（件）与时间x（分）之间的函数解析式为：y＝kx+b（k≠0），把点（0，40），（60，400）代入解析式求出k、b的值即可；
（2）根据“经过多少分钟时，两仓库快递件数相同”可知此时两函数x、y的值相同，联立方程组求出x、y的值即可．
【解答】解：（1）设甲仓库揽收快件y（件）与时间x（分）之间的函数解析式为：y＝kx+b（k≠0），
∵y＝kx+b过点（0，40），（60，400），
∴，
解得，
∴甲仓库揽收快件y（件）与时间x（分）之间的函数解析式为y＝6x+40（0＜x＜60）；
（2）根据题意联立方程组得：
，
解得，
答：经过20分钟时，两仓库快递件数相同，都是160件．
23．（8分）为了响应“足球进学校”的号召，某学校准备到体育用品批发市场购买A型号与B型号两种足球，其中A型号足球的批发价是每个200元，B型号足球的批发价是每个250元，该校需购买A，B两种型号足球共100个．
（1）若该校购买A，B两种型号足球共用了22000元，则分别购买两种型号足球多少个？
（2）若该校计划购进A型号足球的数量不多于B型号足球数量的9倍，请求出最省钱的购买方案，并说明理由．
【分析】（1）设购买A型号足球x个，B型号足球y个，根据总价＝单价×数量结合22000元购买A，B两种型号足球共100个，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设购买A型号足球m个，总费用为w元，则购买B型号足球（100﹣m）个，根据总价＝单价×数量可得出w关于m的函数关系式，由购进A型号足球的数量不多于B型号足球数量的9倍可得出关于m的一元一次不等式，解之即可得出m的取值范围，再利用一次函数的性质即可解决最值问题．
【解答】解：（1）设购买A型号足球x个，B型号足球y个，
依题意，得：，
解得：．
答：该校A型号足球60个，B型号足球40个．
（2）设购买A型号足球m个，总费用为w元，则购买B型号足球（100﹣m）个，
依题意，得：w＝200m+250（100﹣m）＝﹣50m+25000．
∵购进A型号足球的数量不多于B型号足球数量的9倍，
∴m≤9（100﹣m），
∴m≤90．
∵﹣50＜0，
∴w随m的增大而减小，
∴当m＝90时，w取得最小值，
∴最省钱的购买方案为：购买A型号足球90个、B型号足球10个．
五、解答题（三）（本大题2小题，每小题10分，共20分）
24．（10分）如图，直线y＝x﹣2与x轴y轴分别交于A、B两点在y轴上有一点C（0，4），D是OA上一点．
（1）点A的坐标： （4，0） ；点B的坐标 （0，﹣2） ；
（2）若△COD≌△AOB，求直线CD的表达式；
（3）在（2）的条件下，x轴上是否存在点P，使得△PCD是等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
【分析】（1）令x＝0，求y的值得到点B的坐标；令y＝0，由x﹣2＝0求出x的值，得到点A的坐标；
（2）根据三角形全等的判定定理得，OD＝OB，求出点D的坐标，再用待定系数法求出直线CD的表达式；
（3）按PD、PC、CD为底边分类讨论，求出所有符合条件的点P的坐标即可．
【解答】解：（1）令y＝0，由x﹣2＝0，得x＝4，
∴A（4，0）；
当x＝0时，y＝﹣2，
∴B（0，﹣2）．
故答案为：（4，0）；（0，﹣2）．
（2）如图1，作直线CD，射直线CD的函数表达式为y＝kx+b，
∵△COD≌△AOB，
∴OD＝OB＝2，
∵D是OA上一点，
∴D（2，0）；
把C（0，4）、D（2，0）代入y＝kx+b得，
，
∴直线CD的表达式为y＝﹣2x+4．
（3）存在，如图2，PC＝DC，则CO垂直平分PD，
∴OP＝OD＝2，
∴P（﹣2，0）；
如图3，PD＝CD，点P与点O在直线CD的同侧，
∵OD＝2，OC＝4，∠COD＝90°，
∴CD＝＝，
∴PD＝，
∴xP＝2﹣，
∴P（2﹣，0）；
如图4，PD＝CD，点P与点O在直线CD的异侧，
∵PD＝CD＝，
∴xP＝2+，
∴P（2+，0）；
如图5，PC＝PD，
∵PD＝PO+OD＝PO+2，
∴PC＝PO+2，
∵∠POC＝90°，
∴PC2＝PO2+OC2，
∴（PO+2）2＝PO2+42，
解得，PO＝3，
∴P（﹣3，0）．
综上所述，点P的坐标为（﹣2，0）或（2﹣，0）或（2+，0）或（﹣3，0）．
25．（10分）如图，在四边形ABCD中，AB＝AD，∠DAB＝90°，AC平分∠DAB，作DE∥BC交AC于点E，连接BE．
（1）求证：△ADE≌△ABE；
（2）求证：四边形DEBC是菱形；
（3）若∠CDE＝2∠EDA，CE＝2，求AD的长．
【分析】（1）由“SAS”可证△ADE≌△ABE；
（2）由“SAS”可证△BCF≌△DEF，可得BC＝DE，且BC∥DE，DE＝BE，可得结论；
（3）过点E作EH⊥AD于点H，由菱形的性质和角平分线的性质可得EF＝EH＝EC＝，再根据勾股定理可得AE的长，从而可得AF的长，根据三角形AFD是等腰直角三角形，即可得AD的长．
【解答】证明：（1）∵AB＝AD，∠DAB＝90°，
∴△ABD是等腰直角三角形，
∵AC平分∠DAB，
∴∠BAC＝∠DAC＝45°，
∴F是BD的中点，
∴BF＝DF，
在△AED和△AEB中，
，
∴△AED≌△AEB（SAS）；
（2）如图，连接BD交AC于点F，
∵△AED≌△AEB，
∴DE＝BE，
∵DE∥BC，
∴∠CBF＝∠EDF，
在△BCF和△DEF中，
，
∴△BCF≌△DEF（SAS），
∴BC＝DE，
∵BC∥DE，
∴四边形DEBC是平行四边形，
∵BE＝DE，
∴四边形DEBC是菱形；
（3）如图，过点E作EH⊥AD于点H，
∵四边形DEBC是菱形，
∴∠CDB＝∠EDB＝∠CDE，
∵∠CDE＝2∠EDA，
∴∠BDE＝∠ADE，
∵BD⊥CE，EH⊥AD，
∴EF＝EH＝EC＝，
∴AH＝EH＝，
∴AE＝＝＝2，
∴AF＝AE+EF＝2+，
∴DF＝AF＝2+，
∴AD＝AF＝（2+）＝2+2．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/8/16 23:22:50；用户：节节高5；邮箱：5jiejg@xyh.cm；学号：37675298