2020-2021学年山东省临沂市蒙阴县七年级（下）期末数学试卷

这是一份2020-2021学年山东省临沂市蒙阴县七年级（下）期末数学试卷，共18页。

A．﹣6B．36C．±D．±6
2．（3分）下列说法不正确的是（ ）
A．0的立方根是0B．0的平方根是0
C．1的立方根是±1D．4的平方根是±2
3．（3分）在平面直角坐标系中，点M（﹣3，2）向右平移4个单位长度，向下平移3个单位长度后的对应点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．（3分）不等式x+5＜2的解集在数轴上表示为（ ）
A．B．
C．D．
5．（3分）若x＞y，则下列式子中错误的是（ ）
A．x+＞y+B．﹣3x＞﹣3yC．＞D．x﹣3＞y﹣3
6．（3分）如图，在数轴上标有字母的各点中，与实数对应的点是（ ）
A．AB．BC．CD．D
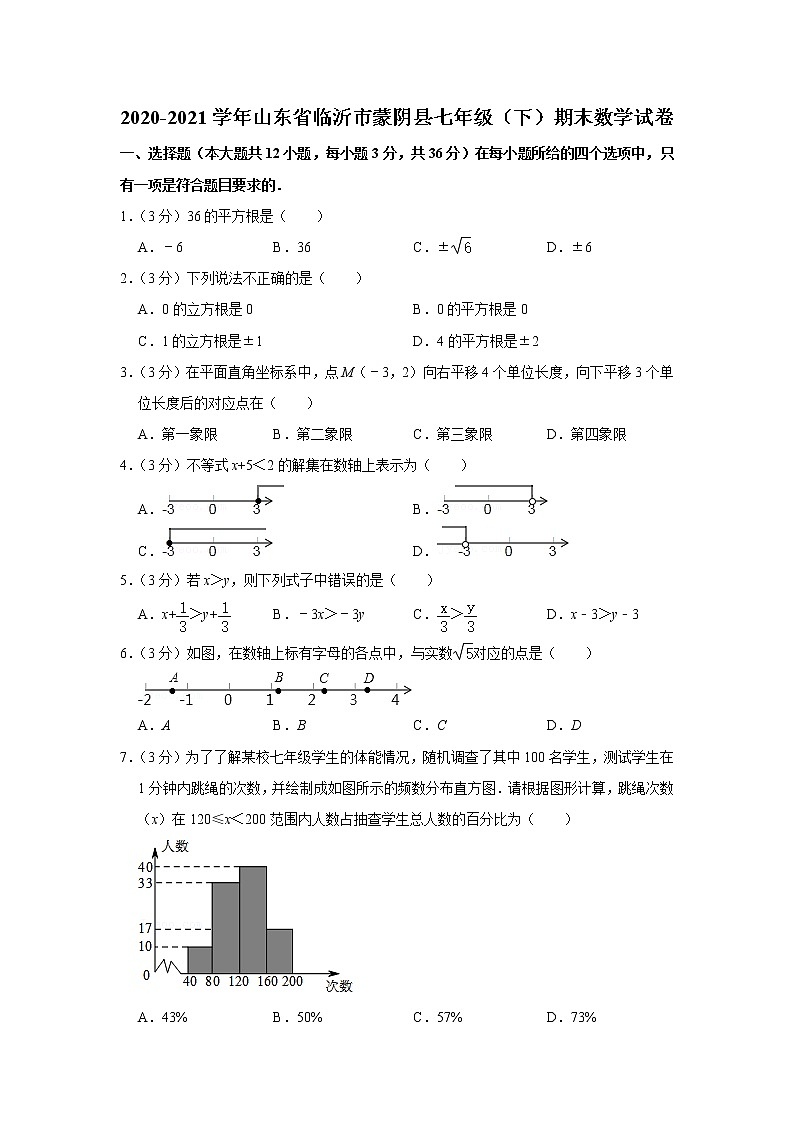
7．（3分）为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图．请根据图形计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为（ ）
A．43%B．50%C．57%D．73%
8．（3分）如图，AB∥CD，DE⊥CE，∠1＝34°，则∠DCE的度数为（ ）
A．56°B．66°C．54°D．34°
9．（3分）已知实数x，y满足，则x﹣y等于（ ）
A．3B．﹣3C．1D．﹣1
10．（3分）甲仓库乙仓库共存粮450吨，现从甲仓库运出存粮的60%，从乙仓库运出存粮的40%．结果乙仓库所余的粮食比甲仓库所余的粮食多30吨．若设甲仓库原来存粮x吨，乙仓库原来存粮y吨，则有（ ）
A．
B．
C．
D．
11．（3分）若不等式组无解，则实数a的取值范围是（ ）
A．a≥﹣1B．a＜﹣1C．a≤1D．a≤﹣1
12．（3分）如图1是长方形纸带，∠DEF＝10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（ ）
A．160°B．150°C．120°D．110°
二、填空题（每小题3分，共18分）请将答案直接写在答题卡中的横线上
13．（3分）计算：＝ ．
14．（3分）点P在第四象限，P到x轴的距离为4，P到y轴距离为3，则点P的坐标为 ．
15．（3分）不等式﹣3x+6＞0的正整数解有 ．
16．（3分）如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB＝ 度．
17．（3分）已知三条不同的直线a、b、c在同一平面内，下列四条命题：
①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．
其中真命题的是 ．（填写所有真命题的序号）
18．（3分）对于实数a，b，定义运算“*”：a*b＝，例如：4*2，因为4＞2，所以4*2＝42﹣4×2＝8．若x，y是二元一次方程组的解，则x*y＝ ．
三．解答题（本大题共7小题，共66分）
19．（9分）解答下列各题：
（1）计算：|﹣|﹣﹣|﹣2|；
（2）求不等式组的解集．
20．（7分）关于x、y的方程组的解是，求|m﹣n|的值．
21．（8分）如图，BCE、AFE是直线，AB∥CD，∠1＝∠2，∠3＝∠4，问AD与BE平行吗？说说你的理由．
22．（10分）在下列网格中建立平面直角坐标系如图，每个小正方形的边长均为1个单位长度．已知A（1，1）、B（3，4）和C（4，2）．
（1）在图中标出点A、B、C．
（2）将点C向下平移3个单位到D点，将点A先向左平移3个单位，再向下平移1个单位到E点，在图中标出D点和E点．
（3）求△EBD的面积S△EBD．
23．（10分）某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：
（1）该商场购进甲、乙两种矿泉水各多少箱？
（2）全部售完500箱矿泉水，该商场共获得利润多少元？
24．（10分）中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
请根据所给信息，解答下列问题：
（1）m＝ ，n＝ ；
（2）请补全频数分布直方图；
（3）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
25．（12分）我县教育局近期下发紧急文件﹣﹣“开展大课间操”活动，某校为开展好大课间活动，欲购买若干个篮球和排球，七年级一班用200元买了2个篮球和2个排球，七年级二班用320元买了3个篮球和4个排球．
（1）求每个篮球、排球的价格；
（2）如果学校购买两种球共100个，总费用不超过6620元，并且篮球数不少于排球数的3倍，那么有几种购买方案？
（3）从节约开支的角度看，你认为采用哪种方案更合算？
2020-2021学年山东省临沂市蒙阴县七年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共12小题，每小题3分，共36分）在每小题所给的四个选项中，只有一项是符合题目要求的．
1．（3分）36的平方根是（ ）
A．﹣6B．36C．±D．±6
【分析】依据平方根的定义求解即可．
【解答】解：∵（±6）2＝36，
∴36的平方根是±6．
故选：D．
2．（3分）下列说法不正确的是（ ）
A．0的立方根是0B．0的平方根是0
C．1的立方根是±1D．4的平方根是±2
【分析】依据平方根、立方根的性质解答即可．
【解答】解：0的立方根是0，故A正确，与要求不符；
0的平方根是0，故B正确，与要求不符；
1的立方根是1，故C错误，与要求相符；
4的平方根是±2，故D正确，与要求不符．
故选：C．
3．（3分）在平面直角坐标系中，点M（﹣3，2）向右平移4个单位长度，向下平移3个单位长度后的对应点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【分析】根据平移的方法结合平移中点的坐标变换规律：横坐标右移加，左移减；纵坐标上移加，下移减，可以直接算出平移后点的坐标．
【解答】解：将点P（﹣3，2）向右平移4个单位长度，再向下平移3个单位长度所得点的坐标为（1，﹣1）；
∴点（1，﹣1）在第四象限，
故选：D．
4．（3分）不等式x+5＜2的解集在数轴上表示为（ ）
A．B．
C．D．
【分析】先求出不等式的解集，再在数轴上表示出来即可．
【解答】解：移项得，x＜2﹣5，
合并同类项得，x＜﹣3，
在数轴上表示为；
故选：D．
5．（3分）若x＞y，则下列式子中错误的是（ ）
A．x+＞y+B．﹣3x＞﹣3yC．＞D．x﹣3＞y﹣3
【分析】根据不等式的性质逐个判断即可．①不等式的性质1：不等式的两边都加（或减）同一个数或式子，不等号的方向不变；②不等式的性质2：不等式的两边都乘以（或除以）同一个正数，不等号的方向不变；③不等式的性质3：不等式的两边都乘以（或除以）同一个负数，不等号的方向改变．
【解答】解：A．∵x＞y，
∴，故本选项不合题意；
B．∵x＞y，
∴﹣3x＜﹣3y，故本选项符合题意；
C．∵x＞y，
∴，故本选项不合题意；
D．∵x＞y，
∴x﹣3＞y﹣3，故本选项不合题意；
故选：B．
6．（3分）如图，在数轴上标有字母的各点中，与实数对应的点是（ ）
A．AB．BC．CD．D
【分析】先估算出的取值范围，进而可得出结论．
【解答】解：∵4＜5＜9，
∴2＜＜3．
故选：C．
7．（3分）为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图．请根据图形计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为（ ）
A．43%B．50%C．57%D．73%
【分析】用120≤x＜200范围内人数除以总人数即可．
【解答】解：总人数为10+33+40+17＝100人，
120≤x＜200范围内人数为40+17＝57人，
在120≤x＜200范围内人数占抽查学生总人数的百分比为＝57%．
故选：C．
8．（3分）如图，AB∥CD，DE⊥CE，∠1＝34°，则∠DCE的度数为（ ）
A．56°B．66°C．54°D．34°
【分析】利用平行线的性质：两直线平行，内错角相等，∠1＝∠CDE，求解．
【解答】解：∵AB∥CD，
∴∠1＝∠CDE＝34°，
∵DE⊥CE，
∴∠CED＝90°，
∴∠DCE＝90°﹣34°＝56°，
故选：A．
9．（3分）已知实数x，y满足，则x﹣y等于（ ）
A．3B．﹣3C．1D．﹣1
【分析】根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．
【解答】解：根据题意得，x﹣2＝0，y+1＝0，
解得x＝2，y＝﹣1，
所以，x﹣y＝2﹣（﹣1）＝2+1＝3．
故选：A．
10．（3分）甲仓库乙仓库共存粮450吨，现从甲仓库运出存粮的60%，从乙仓库运出存粮的40%．结果乙仓库所余的粮食比甲仓库所余的粮食多30吨．若设甲仓库原来存粮x吨，乙仓库原来存粮y吨，则有（ ）
A．
B．
C．
D．
【分析】要求甲，乙仓库原来存粮分别为多少，就要先设出未知数，找出题中的等量关系列方程求解．题中的等量关系为：从甲仓库运出存粮的60%，从乙仓库运出存粮的40%．结果乙仓库所余的粮食比甲仓库所余的粮食多30吨，甲仓库、乙仓库共存粮450吨．
【解答】解：设甲仓库原来存粮x吨，乙仓库原来存粮y吨．
根据题意得：．
故选：C．
11．（3分）若不等式组无解，则实数a的取值范围是（ ）
A．a≥﹣1B．a＜﹣1C．a≤1D．a≤﹣1
【分析】分别求出各不等式的解集，再与已知不等式组无解相比较即可得出a的取值范围．
【解答】解：，
由①得，x≥﹣a，
由②得，x＜1，
∵不等式组无解，
∴﹣a≥1，
解得：a≤﹣1．
故选：D．
12．（3分）如图1是长方形纸带，∠DEF＝10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（ ）
A．160°B．150°C．120°D．110°
【分析】由矩形的性质可知AD∥BC，由此可得出∠BFE＝∠DEF＝10°，再根据翻折的性质可知每翻折一次减少一个∠BFE的度数，由此即可算出∠CFE度数．
【解答】解：∵四边形ABCD为长方形，
∴AD∥BC，
∴∠BFE＝∠DEF＝10°．
由翻折的性质可知：图2中，∠EFC＝180°﹣∠BFE＝170°，∠BFC＝∠EFC﹣∠BFE＝160°，
∴图3中，∠CFE＝∠BFC﹣∠BFE＝150°．
故选：B．
二、填空题（每小题3分，共18分）请将答案直接写在答题卡中的横线上
13．（3分）计算：＝ ﹣2 ．
【分析】因为﹣2的立方是﹣8，所以的值为﹣2．
【解答】解：＝﹣2．
故答案为：﹣2．
14．（3分）点P在第四象限，P到x轴的距离为4，P到y轴距离为3，则点P的坐标为 （3，﹣4） ．
【分析】根据点在第四象限的特点是（+，﹣）解答．
【解答】解：∵点P在第四象限，
∴点P的横坐标为正数，纵坐标为负数，
∵点P到y轴的距离是3，点P到x轴的距离是4，
∴点P的横坐标是3，纵坐标是﹣4，
∴点P的坐标是（3，﹣4）．
15．（3分）不等式﹣3x+6＞0的正整数解有 1 ．
【分析】首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的正整数即可．
【解答】解：移项得：﹣3x＞﹣6，
系数化为1得：x＜2，
则正整数解为：1．
故答案为：1．
16．（3分）如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB＝ 70 度．
【分析】先求出∠CAB及∠ABC的度数，再根据三角形内角和是180°即可进行解答．
【解答】解：连接AB．
∵C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，
∴∠CAB+∠ABC＝180°﹣（45°+25°）＝110°，
∵三角形内角和是180°，
∴∠ACB＝180°﹣（∠CAB+∠ABC）＝180°﹣110°＝70°．
故答案为：70．
17．（3分）已知三条不同的直线a、b、c在同一平面内，下列四条命题：
①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．
其中真命题的是 ①②④ ．（填写所有真命题的序号）
【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．
【解答】解：①如果a∥b，a⊥c，那么b⊥c是真命题，故①正确；
②如果b∥a，c∥a，那么b∥c是真命题，故②正确；
③如果b⊥a，c⊥a，那么b⊥c是假命题，故③错误；
④如果b⊥a，c⊥a，那么b∥c是真命题，故④正确．
故答案为：①②④．
18．（3分）对于实数a，b，定义运算“*”：a*b＝，例如：4*2，因为4＞2，所以4*2＝42﹣4×2＝8．若x，y是二元一次方程组的解，则x*y＝ ﹣3 ．
【分析】利用加减消元法解出方程组的解，根据2＜3，用第二个表达式计算即可．
【解答】解：，
①+②得：3x＝6，
∴x＝2，
代入①得：y＝3，
∵2＜3，
∴原式＝2×3﹣32＝6﹣9＝﹣3．
故答案为：﹣3．
三．解答题（本大题共7小题，共66分）
19．（9分）解答下列各题：
（1）计算：|﹣|﹣﹣|﹣2|；
（2）求不等式组的解集．
【分析】（1）直接利用绝对值的性质以及二次根式的加减运算法则计算得出答案；
（2）分别解不等式，进而得出不等式组的解集．
【解答】解：（1）原式＝
＝﹣2﹣2+
＝﹣4+2；
（2），
由①得，x＞2，
由②得，x≤8，
所以不等式组的解集为：2＜x≤8．
20．（7分）关于x、y的方程组的解是，求|m﹣n|的值．
【分析】根据方程组的解的定义，将方程组的解代入原方程组求出m，n的值，代入即可．
【解答】解∵x、y的方程组的解是，
∴，
∴，
∴|m﹣n|＝|2﹣3|＝1．
21．（8分）如图，BCE、AFE是直线，AB∥CD，∠1＝∠2，∠3＝∠4，问AD与BE平行吗？说说你的理由．
【分析】根据平行线的性质得出∠1＝∠ACD，根据三角形外角性质得出∠3＝∠E+∠CAF，∠4＝∠ACD+∠CAF，求出∠2＝∠E，根据平行线的判定得出即可．
【解答】解：AD∥BE，
理由是：∵AB∥CD，
∴∠1＝∠ACD，
∵∠3＝∠E+∠CAF，∠4＝∠ACD+∠CAF，∠3＝∠4，
∴∠1＝∠E＝∠ACD，
∵∠1＝∠2，
∴∠2＝∠E，
∴AD∥BE．
22．（10分）在下列网格中建立平面直角坐标系如图，每个小正方形的边长均为1个单位长度．已知A（1，1）、B（3，4）和C（4，2）．
（1）在图中标出点A、B、C．
（2）将点C向下平移3个单位到D点，将点A先向左平移3个单位，再向下平移1个单位到E点，在图中标出D点和E点．
（3）求△EBD的面积S△EBD．
【分析】（1）直接利用A，B，C点的坐标在坐标系中得出各点位置；
（2）利用平移的性质得出各对应点位置；
（3）利用△EBD所在矩形面积减去周围三角形面积进而得出答案．
【解答】解：（1）如图所示：A、B、C即为所求；
（2）如图所示：点D，E即为所求；
（3）S△EBD＝5×6﹣×4×5﹣×1×5﹣×1×6＝14.5．
23．（10分）某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：
（1）该商场购进甲、乙两种矿泉水各多少箱？
（2）全部售完500箱矿泉水，该商场共获得利润多少元？
【分析】（1）设商场购进甲种矿泉水x箱，购进乙种矿泉水y箱，根据投入13800元资金购进甲、乙两种矿泉水共500箱，列出方程组解答即可；
（2）总利润＝甲的利润+乙的利润．
【解答】解：（1）设商场购进甲种矿泉水x箱，购进乙种矿泉水y箱，由题意得
，
解得：．
答：商场购进甲种矿泉水300箱，购进乙种矿泉水200箱．
（2）300×（36﹣24）+200×（48﹣33）
＝3600+3000
＝6600（元）．
答：该商场共获得利润6600元．
24．（10分）中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
请根据所给信息，解答下列问题：
（1）m＝ 70 ，n＝ 0.2 ；
（2）请补全频数分布直方图；
（3）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
【分析】（1）根据题意和统计表中的数据可以求得m、n的值；
（2）根据（1）中求得的m的值，从而可以将条形统计图补充完整；
（3）根据统计表中的数据可以估计该校参加这次比赛的3000名学生中成绩“优”等约有多少人．
【解答】解：（1）由题意可得，
m＝200×0.35＝70，n＝40÷200＝0.2，
故答案为：70，0.2；
（2）由（1）知，m＝70，
补全的频数分布直方图，如右图所示；
（3）由题意可得，
该校参加这次比赛的3000名学生中成绩“优”等约有：3000×0.25＝750（人），
答：该校参加这次比赛的3000名学生中成绩“优”等约有750人．
25．（12分）我县教育局近期下发紧急文件﹣﹣“开展大课间操”活动，某校为开展好大课间活动，欲购买若干个篮球和排球，七年级一班用200元买了2个篮球和2个排球，七年级二班用320元买了3个篮球和4个排球．
（1）求每个篮球、排球的价格；
（2）如果学校购买两种球共100个，总费用不超过6620元，并且篮球数不少于排球数的3倍，那么有几种购买方案？
（3）从节约开支的角度看，你认为采用哪种方案更合算？
【分析】（1）设每个篮球的价格为x元，每个排球的价格为y元，根据“七年级一班用200元买了2个篮球和2个排球，七年级二班用320元买了3个篮球和4个排球”，即可得出关于x，y的二元一次方程组，解之即可求出每个篮球、排球的价格；
（2）设购买排球m个，则购买篮球（100﹣m）个，根据“总费用不超过6620元，并且篮球数不少于排球数的3倍”，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为整数，即可得出购买方案的个数；
（3）利用总价＝单价×数量，可分别求出采用各方案所需费用，比较后即可得出结论．
【解答】解：（1）设每个篮球的价格为x元，每个排球的价格为y元，
依题意得：，
解得：．
答：每个篮球的价格为80元，每个排球的价格为20元．
（2）设购买排球m个，则购买篮球（100﹣m）个，
依题意得：，
解得：23≤m≤25．
又∵m为整数，
∴m可以取23，24，25，
∴共有3种购买方案．
（3）当购买23个排球时，100﹣m＝100﹣23＝77，总费用为23×20+77×80＝6620（元）；
当购买24个排球时，100﹣m＝100﹣24＝76，总费用为24×20+76×80＝6560（元）；
当购买25个排球时，100﹣m＝100﹣25＝75，总费用为25×20+75×80＝6500（元）．
∵6620＞6560＞6500，
∴购买排球25个，篮球75个时更合算．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/8/16 23:15:48；用户：节节高5；邮箱：5jiejg@xyh.cm；学号：37675298类别/单价
成本价
销售价（元/箱）
甲
24
36
乙
33
48
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
30
0.15
70≤x＜80
40
n
80≤x＜90
m
0.35
90≤x≤100
50
0.25
类别/单价
成本价
销售价（元/箱）
甲
24
36
乙
33
48
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
30
0.15
70≤x＜80
40
n
80≤x＜90
m
0.35
90≤x≤100
50
0.25