2018_2019学年广州市天河区九上期末数学试卷

这是一份2018_2019学年广州市天河区九上期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列图形是中心对称图形而不是轴对称图形的是
A. B.
C. D.

2. 下列事件是必然事件的是
A. 抛掷一枚硬币四次，有两次正面朝上
B. 打开电视频道，正在播放《今日在线》
C. 射击运动员射击一次，命中十环
D. 方程 x2−x=0 必有实数根

3. 对于二次函数 y=x−12+2 的图象，下列说法正确的是
A. 开口向下B. 对称轴是直线 x=−1
C. 顶点坐标是 1,2D. 与 x 轴有两个交点

4. 某反比例函数的图象经过点 −2,3，则该图象一定不经过点
A. 1,6B. −1,6C. 2,−3D. 3,−2

5. RtABC 中，∠C=90∘，AC=8 cm，BC=6 cm，以点 C 为圆心，5 cm 为半径的圆与直线 AB 的位置关系是
A. 相切B. 相交C. 相离D. 无法确定

6. 下列一元二次方程中，两个实数根之和为 1 的是
A. x2+x+2=0B. x2+x−2=0C. x2−x+2=0D. x2−x−2=0

7. 一种药品原价每盒 25 元，经过两次降价后每盒 16 元，设两次降价的百分率都为 x，则 x 满足等式
A. 161+2x=25B. 251−2x=16
C. 251−x2=16D. 161+x2=25

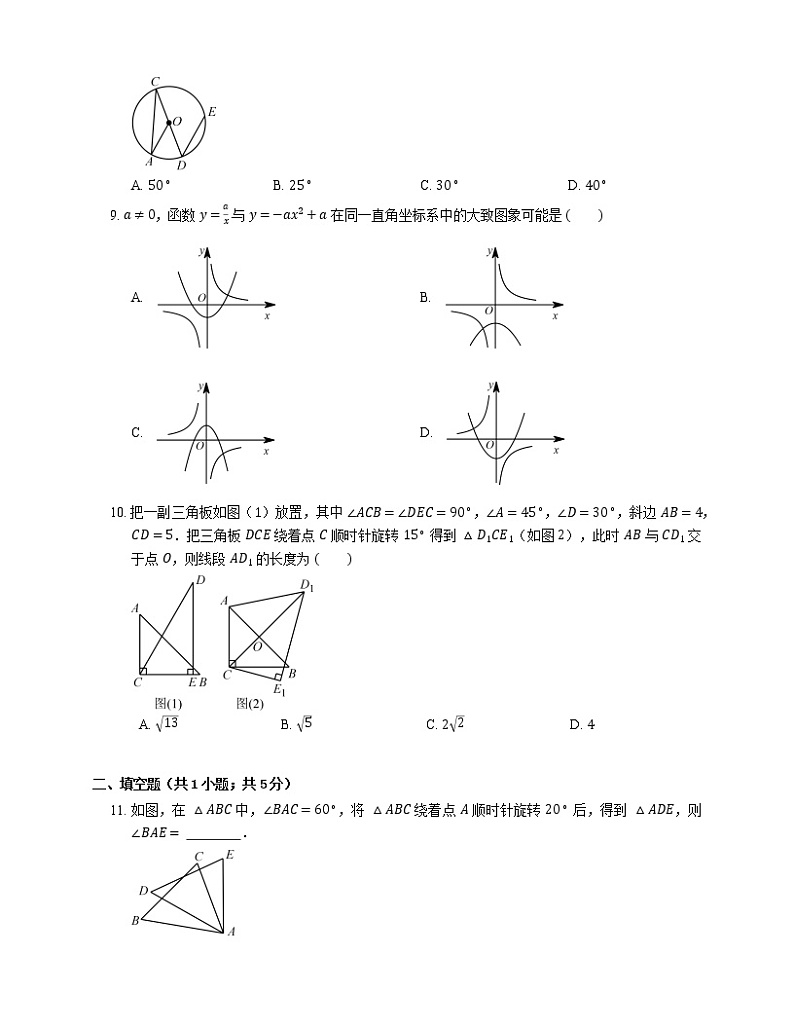
8. 如图，已知 CD 为 ⊙O 的直径，过点 D 的弦 DE 平行于半径 OA，若 ∠D=50∘，则 ∠C 的度数是
A. 50∘B. 25∘C. 30∘D. 40∘

9. a≠0，函数 y=ax 与 y=−ax2+a 在同一直角坐标系中的大致图象可能是
A. B.
C. D.

10. 把一副三角板如图（1）放置，其中 ∠ACB=∠DEC=90∘，∠A=45∘，∠D=30∘，斜边 AB=4，CD=5．把三角板 DCE 绕着点 C 顺时针旋转 15∘ 得到 △D1CE1（如图 2），此时 AB 与 CD1 交于点 O，则线段 AD1 的长度为
A. 13B. 5C. 22D. 4

二、填空题（共1小题；共5分）
11. 如图，在 △ABC 中，∠BAC=60∘，将 △ABC 绕着点 A 顺时针旋转 20∘ 后，得到 △ADE，则 ∠BAE= ．

三、解答题（共1小题；共13分）
12. 已知方程 x2+mx+3=0 的一个根是 x=1，则它的另一个根是 ．

四、填空题（共4小题；共20分）
13. 袋中装有 6 个黑球和 n 个白球，经过若干次试验，发现“若从中任摸一个球，恰好是白球的概率为 14”，则这个袋中白球大约有 个．

14. 如图，已知圆锥的母线长为 2，高所在直线与母线的夹角为 30∘，则圆锥的侧面积为 ．

15. 如图，点 P1,2 在反比例函数的图象上，当 x<1 时，y 的取值范围是 ．

16. 如图是二次函数 y=ax2+bx+c 图象的一部分，图象过点 A−3,0，对称轴为直线 x=−1，给出以下结论：
① abc<0；② b2−4ac>0；③ 4b+c<0；④若 B−52,y1 、 C−12,y2 为函数图象上的两点，则 y1>y2；⑤当 −3≤x≤1 时，y≥0．
其中正确的结论是 ．（填写代表正确结论的序号）

五、解答题（共9小题；共117分）
17. （1）解方程：x2−8x+1=0．
（2）若方程 x2−4x−5=0 的两根分别为 x1，x2，求 x12+x22 的值．

18. 如图，若等腰三角形 ABC 中，AB=AC，点 O 是底边 BC 的中点，⊙O 与腰 AB 相切于点 D，求证：AC 与 ⊙O 相切．

19. 如图，△AOB 的三个顶点都在网格的格点上，网格中的每个小正方形的边长均为一个长度单位，以点 O 为原点建立平面直角坐标系 xOy，若 △AOB 绕点 O 逆时针旋转 90∘ 后，得到 △A1OB1（点 A 和点 A1 是对应点）．
（1）在平面直角坐标系中，画出 △A1OB1，写出点 A1，点 B1 的坐标；
（2）求旋转过程中，边 OB 扫过的面积（结果保留 π）．

20. 摸球活动：在一个口袋中，有四个完全相同的小球，把它们分别标号为 1，2，3，4，随机摸取一个小球，然后放回，再随机摸出一个小球，此活动回答以下问题：
（1）求“两次取的小球标号相同”这个事件的概率；
（2）设计一个概率为 12 的事件，并说明理由．

21. 北方某水果商店从南方购进一种水果，其进货成本是每吨 0.4 万元，根据市场调查，这种水果在北方市场上的销售量为 y（吨），销售价 x（万元）之间的函数关系为 y=−x+2.6．
（1）当每吨销售价为多少万元时，销售利润为 0.96 万元?
（2）填空：当每吨销售价为 万元时，可得最大利润为 万元．

22. 如图，已知点 D 在双曲线 y=20xx>0 的图象上，以点 D 为圆心的 ⊙D 与 y 轴相切于点 C0,4，与 x 轴交于 A，B 两点．
（1）求点 D 的坐标；
（2）求点 A 和点 B 的坐标．

23. 如图，已知二次函数 y=ax2+bx+c 的图象过 A2,0，B0,−1 和 C4,5，与 x 轴的另一个交点为点 D．
（1）求该二次函数的解析式；
（2）求三角形 BDC 的面积．

24. 如图，过 A1,0 作 x 轴的垂线，交反比例函数 y=kxx>0 的图象交于点 M，已知三角形 AOM 的面积为 3．
（1）求 k 的值；
（2）说点 B 的坐标为 t,0，若以 AB 为一边的正方形 ABCD 有顶点在该反比例函数的图象上，求 t 的值．

25. 已知，抛物线 y=x2+bx+c 的顶点为点 D，且经过 A1,0；B0,2 两点，将 △OAB 绕点 A 顺时针旋转 90∘ 后，点 B 落到点 C 的位置，将该抛物线沿着对称轴上下平移，使之经过点 C，此时得到的新抛物线与 y 轴的交点为点 B1，顶点为点 D．
（1）求新抛物线的解析式；
（2）若点 N 在新抛物线上，满足 S△NBB1=2S△NDD1．
答案
第一部分
1. A
2. D【解析】A、抛掷一枚硬币，四次中有两次正面朝上是随机事件，故本选项错误；
B、打开电视频道，正在播放《今日在线》是随机事件，故本选项错误；
C、射击运动员射击一次，命中十环是随机事件，故本选项错误；
D、方程 x2−x=0 必有实数根是必然事件，故本选项正确．
3. C
4. A【解析】∵ 反比例函数的图象经过点 −2,3，
∴k=−2×3=−6，
∴ 反比例函数图象上的点 x,y 的横纵坐标的积是定值 −6，即 xy=−6，
∴ 该图象一定不经过点 1,6．
5. B
【解析】过 C 点作 CD⊥AB，垂足为点 D，
因为 ∠ACB=90∘，BC=6 cm，AC=8 cm，
由勾股定理，得 AB=BC2+AC2=10cm，
根据三角形计算面积的方法可知，12BC⋅AC=12AB⋅CD，
所以 CD=6×810=4.8<5，
所以 ⊙C 与直线 AB 相交．
6. D【解析】A．方程没有实数解，所以A选项错误；
B．两个实数根之和为 −1，所以B选项错误；
C．方程没有实数解，所以C选项错误；
D．两个实数根之和为 1，所以D选项正确．
7. C【解析】第一次降价后的价格为：25×1−x 元；
第二次降价后的价格为：25×1−x2 元；
∵ 两次降价后的价格为 16 元，
∴251−x2=16．
8. B【解析】∵OA∥DE，
∴∠AOD=∠D=50∘，
∴∠C=12∠AOD=25∘．
9. D
10. A
【解析】由题意易知：∠CAB=45∘，∠ACD=30∘．
若旋转角度为 15∘，则 ∠ACO=30∘+15∘=45∘．
所以 ∠AOC=180∘−∠ACO−∠CAO=90∘．
在等腰 Rt△ABC 中，AB=4，则 AC=BC=22．
同理可求得：AO=OC=2．
在 Rt△AOD1 中，OA=2，OD1=CD1−OC=3，
由勾股定理得：AD1=13．
第二部分
11. 80∘
【解析】∵△ABC 绕着点 A 顺时针旋转 20∘ 后得到 △ADE，
∴∠CAE=20∘，
∵∠BAC=60∘，
∴∠BAE=∠BAC+∠CAE=60∘+20∘=80∘．
第三部分
12. x=3
【解析】设方程的另一个根是 x，则 1×x=3，
解得：x=3．
第四部分
13. 2
【解析】∵ 袋中装有 6 个黑球和 n 个白球，
∴ 袋中一共有球 6+n 个，
∵ 从中任摸一个球，恰好是白球的概率为 14，
∴n6+n=14，
解得：n=2．
14. 2π
【解析】如图，
∵AO⊥BC，∠BAO=30∘，
∴OB=12AB=1，
∴ 圆锥的侧面积 =12×2π×1×2=2π．
15. y>2 或 y<0
【解析】当 x<1 时，y>2 或 y<0．
16. ②③⑤
【解析】由图象可知 a<0，b<0，c>0，
∴abc>0，故①错误．
∵ 抛物线与 x 轴有两个交点，
∴b2−4ac>0，故②正确．
∵ 抛物线的对称轴为直线 x=−1，且与 x 轴交于点 A−3,0，
∴ 抛物线与 x 轴的另一个交点为 1,0，
∴a+b+c=0，−b2a=−1，
∴b=2a，c=−3a，
∴4b+c=8a−3a=5a<0，故③正确．
∵B−52,y1 、 C−12,y2 为函数图象上的两点，
又点 C 离对称轴近，
∴y1由图象可知，当 −3≤x≤1 时，y≥0，故⑤正确．
∴ ②③⑤正确．
第五部分
17. （1） 移项可得
x2−8x=−1.
两边加 16 可得
x2−8x+16=−1+16.
配方可得
x−42=15.
两边开方可得
x−4=±15.
所以
x1=4+15,x2=4−15.
（2） 由根与系数的关系，可得 x1+x2=4，x1x2=−5，
所以 x12+x22=x1+x22−2x1x2=42−2×−5=26．
18. 如图，连接 OD，过点 O 作 OE⊥AC 于 E 点，
则 ∠OEC=90∘，
∵AB 切 ⊙O 于点 D，
∴OD⊥AB，
∴∠ODB=90∘，
∴∠ODB=∠OEC，
又 ∵ 点 O 是 BC 的中点，
∴OB=OC，
∵AB=AC，
∴∠B=∠C，
∴△OBD≌△OCEAAS，
∴OE=OD，即 OE 是 ⊙O 的半径，
∴AC 与 ⊙O 相切．
19. （1） 如图，△A1OB1 为所作：
∴ 点 A1 的坐标为 −4,1，点 B1 的坐标为 −3,3．
（2） OB=32+32=32，
∴ 旋转过程中，边 OB 扫过的面积 =90⋅π322360=92π．
20. （1） 树状图如图．
由树状图知，共有 16 种等可能结果，其中两次取的小球标号相同的有 4 种情况，则两次取的小球标号相同的概率为 416=14．
（2） 设计事件：求“两次取出的小球编号和为偶数”这个事件的概率．（答案不唯一）
由（1）中树状图知，共有 16 种等可能结果，其中两次取出的小球的编号和为偶数的情况有 8 种，所以两次取出的小球的编号和为偶数的概率为 12．
21. （1） 设销售利润为 w 万元．
w=x−0.4y=x−0.4−x+2.6=−x2+3x−1.04,
令 w=0.96，则 −x2+3x−1.04=0.96．
解得 x1=1，x2=2．
答：当每吨销售价为 1 万元或 2 万元时，销售利润为 0.96 万元．
（2） 1.5；1.21
【解析】w=−x2+3x−1.04=−x−1.52+1.21.
当 x=1.5 时，w最大=1.21 万元．
∴ 每吨销售价为 1.5 万元时，销售利润最大，最大利润是 1.21 万元．
22. （1） ∵ 以点 D 为圆心的 ⊙D 与 y 轴相切于点 C0,4，
∴ 点 D 的纵坐标为 4，
∵ 点 D 在 y=20x 图象上，
∴4=20x，
∴x=5，
∴D5,4．
（2） 过点 D 作 DE⊥AB 于点 E，连接 AD，BD．
在 Rt△AED 中，DA=5，DE=4，
∴AE=AD2−DE2=3，
∴OA=5−3=2，OB=5+3=8，
∴A2,0，B8,0．
23. （1） 把 A2,0，B0,−1 和 C4,5 三点坐标代入解析式 y=ax2+bx+c 得到：
c=−1,4a+2b+c=0,16a+4b+c=5.
解得 a=12,b=−12,c=−1.
∴ 抛物线的解析式为 y=12x2−12x−1．
（2） 如图，
对于抛物线 y=12x2−12x−1，令 y=0，得 12x2−12x−1=0，解得 x1=2，x2=−1，
∴ 另一个交点为 D 坐标为 −1,0，
∵ 直线 BC 的解析式为 y=32x−1，令 y=0，得 x=23，
设直线 BC 与 x 轴交于点 H，则 H23,0，∴S△BCD=S△DHC+S△DHB=12×53×5+12×53×1=5．
24. （1） 根据题意得 12∣k∣=3，而 k>0，
∴k=6．
（2） ∵ 四边形 ABCD 为正方形，
如图 1，
当 B 点在 A 点左侧时，AB=1−t，则 D1,1−t，所以 1⋅1−t=6，解得 t=−5；
当点 B 在点 A 的右侧，则 AB=t−1，
∴Ct,t−1，D1,t−1，
如图 2，
若 D1,t−1 在反比例函数图象上时，则 t−1=6，解得 t=7；
如图 3，
若 Ct,t−1 在反比例函数图象上时，则 t−1=6t，整理得 t2−t−6=0，解得 t1=3，t2=−2（舍去）；
综上所述，t 的值为 −5 或 3 或 7．
25. （1） 如图，
已知抛物线 y=x2+bx+c 经过 A1,0，B0,2，
∴1+b+c=0,c=2,
解得 b=−3,c=2,
抛物线的解析式为 y=x2−3x+2；
∵A1,0，B0,2，
∴OA=1，OB=2，
可得旋转后 C 点的坐标为 3,1，
当 x=3 时，由 y=x2−3x+2 得 y=2，
可知抛物线 y=x2−3x+2 过点 3,2，
∴ 将原抛物线沿 y 轴向下平移 1 个单位后过点 C．
∴ 平移后的抛物线解析式为：y2=x2−3x+1．
（2） ∵ 点 N 在 y=x2−3x+1 上，可设 N 点坐标为 x0,x02−3x0+1，
将 y=x2−3x+1 配方得 y=x−322−54，
∴ 其对称轴为直线 x=32．
① 0≤x0≤32 时，如图①，
S△NBB1=2S△NDD1，
∴12×1×x0=2×12×1×32−x0，
∵x0=1，
此时 x02−3x0+1=−1，
∴N 点的坐标为 1,−1．
②当 x0>32 时，如图②，
同理可得 12×1×x0=2×12×x0−32，
∴x0=3，
此时 x02−3x0+1=1，
∴ 点 N 的坐标为 3,1．
③当 x<0 时，由图可知，N 点不存在，
综上，点 N 的坐标为 1,−1 或 3,1．