

2018_2019学年北京市门头沟七下期末数学试卷
展开一、选择题(共8小题;共40分)
1. 人的头发粗细各异,普通头发的直径是 0.00008 米,将数字 0.00008 用科学记数法表示为
A. 8×10−6B. 8×10−5C. 0.8×10−5D. 0.8×10−6
2. 已知 x>y,下列变形正确的是
A. x−3
3. 下列各式计算正确的是
A. 2a2+a2=3a4B. a3⋅a2=a6C. a6÷a2=a3D. ab23=a3b6
4. 含 30∘ 角的直角三角板与直线 a,b 的位置关系如图所示,已知 a∥b,∠1=35∘.则 ∠ADC 的度数是
A. 55∘B. 35∘C. 65∘D. 45∘
5. 下列命题属于真命题的是
A. 同旁内角相等,两直线平行
B. 相等的角是对顶角
C. 平行于同一条直线的两条直线平行
D. 同位角相等
6. 利用图中图形面积关系可以解释的公式是
A. a+b2=a2+2ab+b2B. a−b2=a2−2ab+b2
C. a+ba−b=a2−b2D. 2a+b=2a+2b
7. 下列因式分解正确的是
A. a3−2a2−a=aa2−2aB. 4a2−8ab+4b2=2a−2b2
C. x2−4y2=x+4yx−4yD. 5x3−10x2+5x=5xx−12
8. 某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解全校同学的植树情况,学校随机抽查了一部分同学的植树情况,将调查数据整理绘制成如图所示的统计图.下面有四个推断:
①这次调查获取的样本数据的样本容量是 100;
②这次调查获取的样本数据的中位数是 6 棵;
③这次调查获取的样本数据的众数是 4 棵;
④这次调查获取的样本数据的平均数是 8 棵.
其中合理的是
A. ①②B. ①③C. ②③D. ②④
二、填空题(共8小题;共40分)
9. 3−π0= ,12−1= .
10. 如果把方程 2x−y+1=0 写成用含 x 的代数式表示 y 的形式,那么 y= .
11. 如果 ∠1 与 ∠2 互余,∠3 与 ∠4 互余,且 ∠1=∠3,∠2=55∘,那么 ∠4= 度.
12. 已知:如图 △ABC 中,点 D,E,F 分别在 AB,AC,BC 上,连接 DE,BE,EF,要使 DE∥BC,你认为应该添加的条件是 .
13. 《孙子算经》是中国古代重要的数学著作,共三卷.卷上叙述了算筹记数的纵横相间制度和筹算乘除法,卷中举例说明筹算分数算法和筹算开平方法,卷下对后世的影响最深,其中卷下记载这样一道经典的问题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”意思是:“鸡和兔关在一个笼子里,从上面看,有 35 个头;从下面看,有 94 条脚.问笼中各有多少只鸡和多少只兔?”,设有鸡 x 只,兔子 y 只,可列方程组为 .
14. 在数学课上,老师要求同学们利用一副三角板画出两条平行线.
小明的画法如下:
步骤一:运用三角板一边任意画一条直线 l;
步骤二:按如图方式摆放三角板;
步骤三:沿三角板的直角边画出直线 AB,CD;
这样,得到 AB∥CD.
小明这样画图的依据是 .
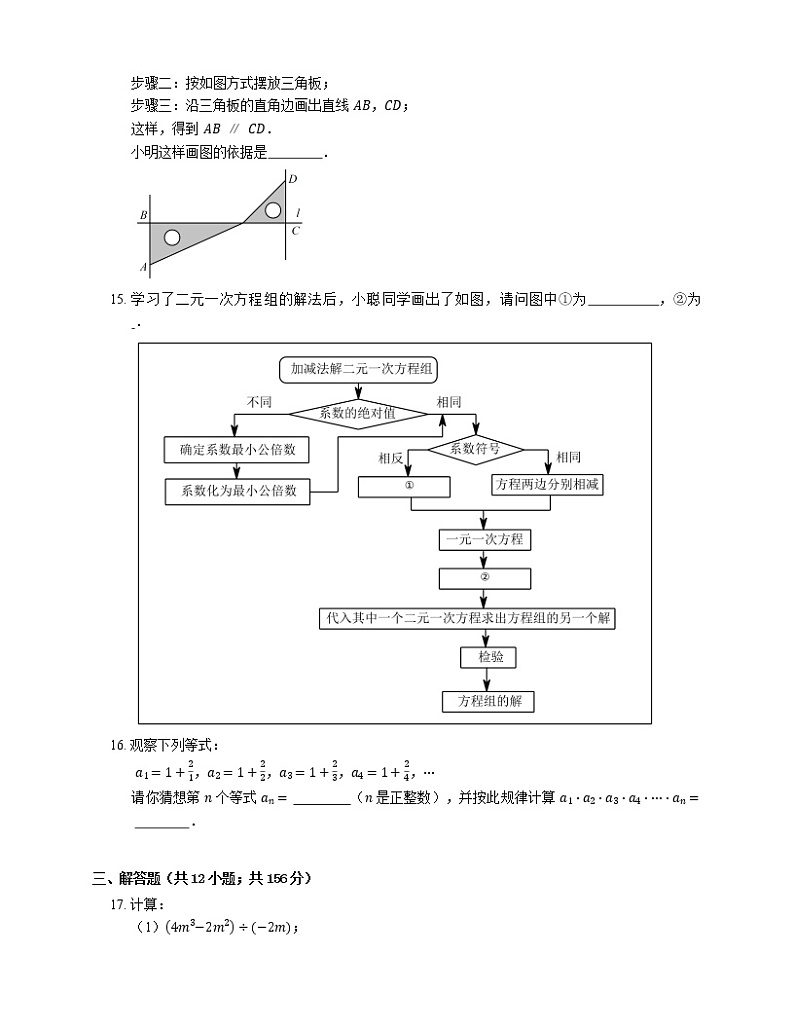
15. 学习了二元一次方程组的解法后,小聪同学画出了如图,请问图中①为 ,②为 .
16. 观察下列等式:
a1=1+21,a2=1+22,a3=1+23,a4=1+24,⋯
请你猜想第 n 个等式 an= (n 是正整数),并按此规律计算 a1⋅a2⋅a3⋅a4⋅⋯⋅an= .
三、解答题(共12小题;共156分)
17. 计算:
(1)4m3−2m2÷−2m;
(2)x+3x−2−x−42.
18. 解下列方程组:
(1)x=1−3y,3x−y=3.
(2)3x−4y=9,2x−3y=7.
19. 因式分解:
(1)2x2−8;
(2)4x2−x2+12.
20. 本学期学习了一元一次不等式的解法,下面是甲同学的解题过程:
解不等式 x−22−1≤5x+14.
解:不等式两边同时乘以 4,得:x−22×4−1≤5x+14×4, ⋯⋯①
去分母,得:2x−2−1≤5x+1, ⋯⋯②
去括号,得:2x−4−1≤5x+1, ⋯⋯③
移项,得:2x−5x≤1+1+4, ⋯⋯④
合并同类项,得:−3x≤6, ⋯⋯⑤
系数化 1,得:x≤−2. ⋯⋯⑥
不等式的解集在数轴上表示为:
上述甲同学的解题过程从第 步开始出现错误,错误的原因是 .
请帮甲同学改正错误,写出完整的解题过程,并把正确解集在数轴上表示出来.
21. 解不等式组 3x+3>4x+7,x−1≥x−73, 并写出它的所有整数解.
22. 完成下面的证明:
已知:如图,点 D,E,F 分别在线段 AB,BC,AC 上,连接 DE,EF,DM 平分 ∠ADE 交 EF 于点 M,∠1+∠2=180∘.
求证:∠B=∠BED.
证明:∵∠1+∠2=180∘(已知),
又 ∵∠1+∠BEM=180∘(平角定义),
∴∠2=∠BEM ,
∴DM∥ .
∴∠ADM=∠B ,
∠MDE=∠BED .
又 ∵DM 平分 ∠ADE(已知),
∴∠ADM=∠MDE(角平分线定义).
∴∠B=∠BED(等量代换).
23. 已知 x2−2x−1=2,求代数式 x−12+xx−4+x−3x+3 的值.
24. 已知:如图,∠1=∠2,∠B=∠C.
(1)求证 AB∥CD;
(2)若 ∠A=30∘,求 ∠D 的度数.
25. 为了丰富学生校园生活,满足学生的多元文化需求,促进学生身心健康和谐发展,学校开展了丰富多彩的社团活动.我区某中学开展的社团活动有A.动漫社团;B.轮滑社团;C.音乐社团;D.诗歌社团;E.书法社团.学生管理中心为了了解全校 500 名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全.
(1)抽样调查:学生管理中心计划选取 40 名学生进行问卷调研,下面的抽样方法中,合理的是 (填序号);
①从九年级 1 班、 2 班各随机抽取 20 名学生进行问卷调研;
②从七、八、九三个年级中随机抽取 40 名女生进行问卷调研;
③从七、八、九三个年级中随机抽取男女生各 20 名进行问卷调研.
(2)收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,A,C,E,D,B,A,B,E,C,A,D,D,B,B,C,C,A,A,E,B,C,B,D,C,A,C,C,A,C,E.
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图.
(3)分析数据、推断结论:
(1)在扇形统计图中,“B轮滑社团”所在的扇形的圆心角等于 度;
(2)请你任选A ∼ E中的一个社团项目,根据学生管理中心获得的样本数据估计全校大约有多少名同学选择这个社团项目.
26. 2018 年 4 月 23 日,第 23 个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为每个班级订购了一批新的图书.初一年级两个班订购图书情况如表:
老舍文集套四大名著套总费用元初一1班42480初一2班23520
(1)求老舍文集和四大名著每套各是多少元;
(2)学校准备再购买老舍文集和四大名著共 10 套,总费用不超过 700 元,问学校有哪几种购买方案.
27. 已知:如图,点 D 是直线 AB 上一动点,连接 CD,过点 D 作 DE∥BC 交直线 AC 于点 E.
(1)如图 1,当点 D 在线段 AB 上时,
①依题意,在图 1 中补全图形;
②若 ∠ABC=100∘,∠BCD=20∘,则 ∠ADC= 度.
(2)当点 D 在线段 AB 的延长线上时,请写出 ∠ADC,∠ABC,∠BCD 的数量关系,并证明.
(3)当点 D 在直线 AB 上时,请直接写出 ∠ADC,∠ABC,∠BCD 的数量关系,不需证明.
28. 定义:对任意一个两位数 a,如果 a 满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与 11 的商记为 fa.
例如:a=12,对调个位数字与十位数字得到新两位数 21,新两位数与原两位数的和为 21+12=33,和与 11 的商为 33÷11=3,所以 f12=3.
根据以上定义,回答下列问题:
(1)填空:①下列两位数:30,31,33 中,“迥异数”为 .
②计算:f23= ,f10m+n= .
(2)如果一个“迥异数”b 的十位数字是 k,个位数字是 2k+1,且 fb=11,请求出“迥异数”b.
(3)如果一个“迥异数”m 的十位数字是 x,个位数字是 x−4,另一个“迥异数”n 的十位数字是 x−5,个位数字是 2,且满足 fm−fn<8,请直接写出满足条件的 x 的值.
答案
第一部分
1. B
2. C
3. D
4. A
5. C
6. A
7. D
8. B
第二部分
9. 1,2
10. 2x+1
11. 55
12. 答案不唯一,例如 ∠ADE=∠ABC
13. x+y=35,2x+4y=94
14. 内错角相等,两直线平行
15. 方程两边分别相加,求解一元一次方程
16. 1+2n,n2+3n+22
第三部分
17. (1) 原式=−2m2+m.
(2) 原式=x2+x−6−x2−8x+16=x2+x−6−x2+8x−16=9x−22.
18. (1)
x=1−3y, ⋯⋯①3x−y=3. ⋯⋯②
把 ① 代入 ② 得
31−3y−y=3.
解得
y=0.
把 y=0 代入 ① 得
x=1−0=1.
所以原方程组的解为
x=1,y=0.
(2)
3x−4y=9, ⋯⋯①2x−3y=7. ⋯⋯②①×2
得
6x−8y=18. ⋯⋯③②×3
得
6x−9y=21. ⋯⋯④③−④
得
−8y+9y=18−21.
解得
y=−3.
把 y=−3 代入 ① 得
3x+12=9.
解得
x=−1.
所以原方程组的解为
x=−1,y=−3.
19. (1) 2x2−8=2x2−4=2x+2x−2.
(2) 4x2−x2+12=2x+x2+12x−x2−1=−2x+x2+1−2x+x2+1=−x+12x−12.
20. ①;利用不等式的性质时漏乘
x−22×4−4≤5x+14×4.2x−2−4≤5x+1.2x−4−4≤5x+1.2x−5x≤1+4+4.−3x≤9.x≥−3.
在数轴上表示为:
21.
3x+3>4x+7, ⋯⋯①x−1≥x−73. ⋯⋯②
由 ① 得
x<2.
由 ② 得
x≥−2.∴
原不等式组的解集是
−2≤x<2.∴
原不等式组的所有整数解为 −2,−1,0,1.
22. 同角的补角相等;BC;同位角相等,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等
23. x−12+xx−4+x−3x+3=x2−2x+1+x2−4x+x2−9=3x2−6x−8,
∵x2−2x−1=2,
∴x2−2x=3,
∴原式=3x2−6x−8=3x2−2x−8=3×3−8=1.
24. (1) ∵ ∠1=∠2,
又 ∵ ∠1=∠FMN,
∴ ∠2=∠FMN,
∴ CF∥BE,
∴ ∠C=∠BED,
又 ∵ ∠B=∠C,
∴ ∠B=∠BED,
∴ AB∥CD.
(2) ∵ AB∥CD,
∴ ∠A=∠D,
又 ∵ ∠A=30∘,
∴ ∠D=30∘.
25. (1) ③
(2) 补全表格和扇形统计图.
(3) (1)90
(2)选择音乐社团.
500×30%=150(名).
答:全校大约有 150 名同学选择音乐社团.
26. (1) 设老舍文集每套 x 元,四大名著每套 y 元.
根据题意,得:
4x+2y=480,2x+3y=520.
解得:
x=50,y=140.
答:老舍文集每套 50 元,四大名著每套 140 元.
(2) 设学校决定购买老舍文集 a 套,则购买四大名著 10−a 套.
由题意,得
50a+14010−a≤700.
解得
a≥709.
根据题意,得:a=8,9,10.
所以,该公司有以下三种方案:
方案 1:购买老舍文集 8 套,四大名著为 2 套;
方案 2:购买老舍文集 9 套,四大名著为 1 套;
方案 3:购买老舍文集 10 套,四大名著为 0 套.
27. (1) ①补全图形,如图 1;
② 120
(2) ∠ADC=∠ABC−∠BCD.
证明:如图 2.
∵DE∥BC,
∴∠ADE=∠ABC,∠CDE=∠BCD.
又 ∵∠ADC=∠ADE−∠CDE,
∴∠ADC=∠ABC−∠BCD.
(3) ∠ADC=∠ABC±∠BCD,∠ADC+∠ABC+∠BCD=180∘.
28. (1) 31;5;m+n
(2) 由题意,得 k+2k+1=11,
解得:k=3.
所以 b=38.
(3) x=6,x=8.
2018_2019学年北京市门头沟八下期末数学试卷: 这是一份2018_2019学年北京市门头沟八下期末数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018_2019学年北京市门头沟区七上期末数学试卷: 这是一份2018_2019学年北京市门头沟区七上期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018_2019学年北京市朝阳区七下期末数学试卷: 这是一份2018_2019学年北京市朝阳区七下期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












