2018_2019学年佛山市禅城区七下期末数学试卷

这是一份2018_2019学年佛山市禅城区七下期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列运算正确的是
A. a4+a5=a9B. a4⋅a2=a8
C. a3÷a3=0D. −a23=−a6

2. 下列各式中，相等关系一定成立的是
A. x+6x−6=x2−6
B. x−y2=y−x2
C. x−2x−6=x2−2x−6x−12
D. x+y2=x2+y2

3. 变量 x 与 y 之间的关系式 y=12x2−2，当自变量 x=2 时，因变量 y 的值是
A. −2B. −1C. 0D. 1

4. 下列事件，是必然事件的有
A. 打开电视，它正在播广告
B. 抛掷一枚硬币，正面朝上
C. 打雷后下雨
D. 367 人中有至少两个人的生日相同

5. 下列正确说法的个数是
①同位角相等；
②对顶角相等；
③等角的补角相等；
④两直线平行，同旁内角相等．
A. 1B. 2C. 3D. 4

6. 如图，用尺规作一个角等于已知角，其作图原理是：由 △ODC≌△OʹDʹCʹ 得 ∠AOB=∠AʹOʹBʹ，其依据的定理是
A. SSSB. SASC. ASAD. AAS

7. 如图，下列推理错误的是
A. ∵∠1=∠3，∴a∥bB. ∵∠1=∠2，∴a∥b
C. ∵∠3=∠5，∴c∥dD. ∵∠2+∠4=180∘，∴c∥d

8. 已知点 P 在直线 MN 外，点 A，B，C 均在直线 MN 上，PA=3 cm，PB=3.5 cm，PC=2 cm，则点 P 到直线 MN 的距离
A. 等于 3 cmB. 等于 2 cmC. 等于 3.5 cmD. 不大于 2 cm

9. 小明做了 6 次掷质地均匀硬币的试验，在前 5 次试验中，有 2 次正面朝上，3 次正面朝下，那么第 6 次试验，硬币正面朝上的概率是
A. 1B. 0C. 0.5D. 不稳定

10. 如图，它表示甲乙两人从同一个地点出发后的情况．根据图象判断，下列说法错误的是
A. 甲是 8 点出发的
B. 乙是 9 点出发的，到 10 点时，他大约走了 10 千米
C. 到 10 点为止，乙的速度快
D. 两人在 12 点再次相遇

二、填空题（共6小题；共30分）
11. 用科学记数法表示 0.0000123 得 ．

12. 在直角三角形中，一个锐角比另外一个锐角的 3 倍还多 10∘，则这两个角分别为 ．

13. 等腰三角形的顶角和一个底角的度数的比是 4:1，则底角的度数为 ．

14. 已知 △ABC 中，AB=2，BC=5，且 AC 的长为偶数，则 AC 的长为 ．

15. 计算：x3−2x÷12x= ．

16. 如果将 a+bn（n 为非负整数）的每一项按字母 a 的次数由大到小排列，可以得到下面的等式（1），然后将每个式子的各项系数排列成（2）：
a+b1=a+b
a+b2=a2+2ab+b2
a+b3=a3+3a2b+3ab2+b3
a+b4=a4+4a3b+6a2b2+4ab3+b4
\[ \begin{array}{ccccccccccc} & & & & 1 & & 1 & & &\\ \\& & & 1 & & 2 & & 1 & &\\ \\ & & 1 & & 3 & & 3 & & 1 &\\ \\& 1 & & 4 & & 6 & & 4 & & 1\\ \\\end{array}\]根据规律可得：a+b5=（ ）

三、解答题（共9小题；共117分）
17. 计算：2−2−−2+π−3.140．

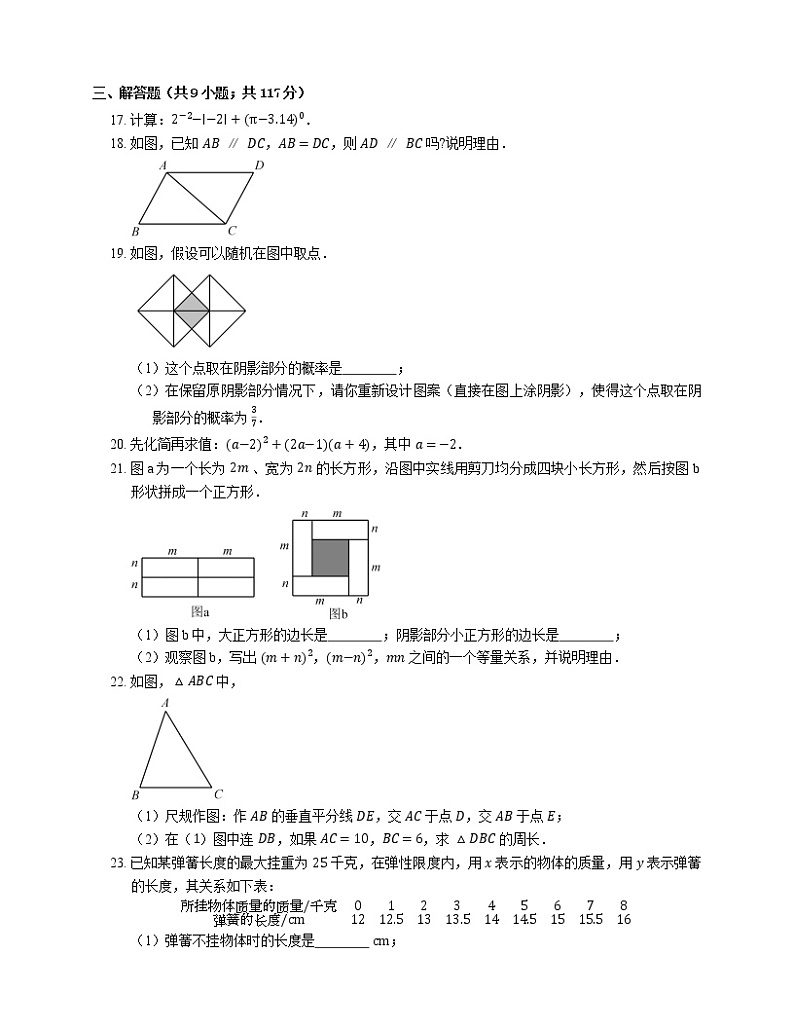
18. 如图，已知 AB∥DC，AB=DC，则 AD∥BC 吗?说明理由．

19. 如图，假设可以随机在图中取点．
（1）这个点取在阴影部分的概率是 ；
（2）在保留原阴影部分情况下，请你重新设计图案（直接在图上涂阴影），使得这个点取在阴影部分的概率为 37．

20. 先化简再求值：a−22+2a−1a+4，其中 a=−2．

21. 图a为一个长为 2m 、宽为 2n 的长方形，沿图中实线用剪刀均分成四块小长方形，然后按图b形状拼成一个正方形．
（1）图b中，大正方形的边长是 ；阴影部分小正方形的边长是 ；
（2）观察图b，写出 m+n2，m−n2，mn 之间的一个等量关系，并说明理由．

22. 如图，△ABC 中，
（1）尺规作图：作 AB 的垂直平分线 DE，交 AC 于点 D，交 AB 于点 E；
（2）在（1）图中连 DB，如果 AC=10，BC=6，求 △DBC 的周长．

23. 已知某弹簧长度的最大挂重为 25 千克，在弹性限度内，用 x 表示的物体的质量，用 y 表示弹簧的长度，其关系如下表：
所挂物体质量的质量/千克012345678弹簧的长度
（1）弹簧不挂物体时的长度是 cm；
（2）随着 x 的变化，y 的变化趋势是： ；
（3）根据表中数据的变化关系，写出 y 与 x 的关系式，并指出自变量的取值范围是 ．

24. 如图，在四边形 ABCD 中，AD∥BC，E 为 CD 的中点，连接 AE，BE，延长 AE 交 BC 的延长线于点 F．
（1）△DAE 和 △CFE 全等吗?说明理由．
（2）若 AB=BC+AD，说明 BE⊥AF．
（3）在（2）的条件下，若 EF=6，CE=5，∠D=90∘，你能否求出 E 到 AB 的距离?如果能请直接写出结果．

25. 如图，已知 △ABC 中，AB=AC=6 cm，BC=4 cm，点 D 为 AB 的中点．如果点 P 在线段 BC 上以 1 cm/s 的速度由 B 点向 C 点运动，同时，点 Q 在线段 CA 上由 C 点向 A 点运动．
（1）若点 Q 的运动速度与点 P 的运动速度相等，经过 1 秒后，△BPD 与 △CQP 是否全等，请说明理由；
（2）若点 Q 的运动速度与点 P 的运动速度不相等，当点 Q 的运动速度为多少时，能够使 △BPD 与 △CQP 全等?
（3）若点 Q 以（2）中的运动速度从点 C 出发，点 P 以原来的运动速度从点 B 同时出发，都逆时针沿 △ABC 三边运动，求经过多长时间点 P 与点 Q 第一次在 △ABC 的哪条边上相遇?
答案
第一部分
1. D【解析】A．∵a4 与 a5 不是同类项，不能合并，故错误；
B．∵a4⋅a2=a6，故错误；
C．a3÷a3=1，故错误；
D．−a23=−a6，故正确．
2. B【解析】A．∵x+6x−6=x2−36，故不成立；
B．∵x−y2=y−x2，故成立；
C．∵x−2x−6=x2−2x−6x+12，故不成立；
D．x+y2=x2+2xy+y2，故不成立．
3. C【解析】x=2 时，y=12×22−2=0．
4. D【解析】A．打开电视，它正在播广告是随机事件；
B．抛掷一枚硬币，正面朝上是随机事件；
C．打雷后下雨是随机事件；
D．∵ 一年有 365 天，
∴367 人中有至少两个人的生日相同是必然事件．
5. B
【解析】∵ 两直线平行，同位角相等，故①错误；
∵ 对顶角相等，故②正确；
∵ 等角的补角相等，故③正确；
∵ 两直线平行，同旁内角互补，故④错误．
∴ 下列正确说法的有②③．
6. A【解析】在 △OCD 与 △OʹCʹDʹ，
∵OʹCʹ=OC,OʹDʹ=OD,CʹDʹ=CD,
∴△OCD≌△OʹCʹDʹSSS，
∴∠AʹOʹBʹ=∠AOB，
显然运用的判定方法是 SSS．
7. A【解析】A．∵∠1 与 ∠3 不具有特殊位置关系，∴ 不能推出 a∥b；
B．∵∠1 与 ∠2 是一对内错角，∴ 由 ∠1=∠2 能推出 a∥b；
C．∵∠3 与 ∠5 是一对同位角，∴ 由 ∠3=∠5 能推出 c∥d；
D．∵∠2 与 ∠4 是一对同旁内角，∴ 由 ∠2+∠4=180∘ 能推出 c∥d．
8. D【解析】∵ 垂线段最短，
又 ∵ 点 P 在直线 MN 外，点 A，B，C 均在直线 MN 上，PA=3 cm，PB=3.5 cm，PC=2 cm，
∴ 点 P 到直线 MN 的距离小于或等于 2 cm，即不大于 2 cm．
9. C【解析】因为一枚质地均匀的硬币只有正反两面，所以不管抛多少次，硬币正面朝上的概率都是 12．
10. B
【解析】从图象可知：甲做变速运动，8 时到 11 时走了 20 千米，速度为每小时 203 千米，11 时到 12 时走了 20 千米，速度为每小时 20 千米；乙做的是匀速运动，9 时到 12 时走了 40 千米，速度是每小时 403 千米．
A．由图象知，甲 8 点出发，故A正确；
B．由图象知，乙 9 点出发；到 10 时他大约走了 13 千米，故B不正确；
C．到 10 时为止，甲的速度为每小时 203 千米，乙的速度是每小时 403 千米，乙的速度快，故C正确；
D．由图象知，两人最终在 12 时相遇，故D正确．
第二部分
11. 1.23×10−5
【解析】0.0000123=1.23×10−5．
12. 20∘，70∘
【解析】设其中一个锐角的度数是 x 度，则另一个锐角的度数就是 3x+10 度，
由题意得，x+3x+10=90，4x=80，x=20，
3x+10=3×20+10=70．
13. 30∘
【解析】∵ 等腰三角形的顶角和它的一个底角的度数比是 4:1，
∴ 它的底角为 180∘×14+1+1=30∘．
14. 4 或 6
【解析】∵AB=2，BC=5，
∴3 ∴ 其中的偶数有：4，6．
15. 2x2−4
【解析】原式=x3−2x×2x=x3×2x−2x×2x=2x2−4.
16. a5+5a4b+10a3b2+10a2b3+5ab4+b5
【解析】由题意每个数字等于上一行的左右两个数字之和，就可以得到 a+b5 的展开式中各项系数，从而可写出结果．
根据题目的特征可得第5行数字从左到右为 1，5，10，10，5，1，
所以 a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5．
第三部分
17. 原式=14−2+1=−34.
18. AD∥BC，理由如下：
∵AB∥DC，
∴∠BAC=∠DCA．
在 △ABC 和 △ACD 中，
AB=CD,∠BAC=∠DCA,AC=CA,
∴△ABC≌△CDASAS，
∴∠ACB=∠DAC，
∴AD∥BC．
19. （1） 17
（2） 如图所示（红色部分），答案不唯一．
20. a−22+2a−1a+4=a2−4a+4+2a2+7a−4=3a2+3a,
当 a=−2 时，
原式=3×−22+3×−2=12−6=6.
21. （1） m+n；m−n
（2） m−n2=m+n2–4mn．
理由如下：
右边=m+n2−4mn=m2+2mn+n2−4mn=m2−2mn+n2=m−n2=左边,
∴ 结论成立．
22. （1） 如图；
（2） 如图：
∵DE 是 AB 的垂直平分线，
∴AD=BD，
∴C△BCD=BD+BC+CD=AD+CD+BC=AC+BC=10+6=16．
23. （1） 12
【解析】由表格知，弹簧不挂物体时的长度是 12 cm．
（2） x 每增加 1 千克，y 增加 0.5 cm
【解析】根据表格数据可知 x 每增加 1 千克，y 增加 0.5 cm．
（3） y=0.5x+12，0≤x≤25
【解析】∵x 每增加 1 千克，y 增加 0.5 cm，
∴y=0.5x+120≤x≤25．
24. （1） △DAE≌△CFE 理由如下：
∵AD∥BC（已知），
∴∠ADC=∠ECF（两直线平行，内错角相等），
∵E 是 CD 的中点（已知），
∴DE=EC（中点的定义）．
∵ 在 △ADE 与 △FCE 中，
∠ADC=∠FCD,DE=CE,∠AED=∠FEC.
∴△ADE≌△FCEASA．
（2） 由（1）得 △ADE≌△FCE，
∴AD=CF，AE=EF（全等三角形的对应边相等），
∴E 为 AF 中点，即 BE 是 △ABF 中 AF 边上的中线，
∵AB=BC+AD，
∴AB=BC+CF=BF，
∴BE⊥AF（三线合一）．
（3） E 到 AB 的距离等于 5．
【解析】∵AD∥BC，∠D=90∘，
∴∠BCE=90∘，
∵CE=5，
∴E 到 AB 的距离等于 5．
25. （1） 全等，理由如下：
∵t=1 秒，
∴BP=CQ=1×1=1cm，
∵AB=6 cm，点 D 为 AB 的中点，
∴BD=3 cm．
又 ∵PC=BC−BP，BC=4 cm，
∴PC=4−1=3cm，
∴PC=BD．
又 ∵AB=AC，
∴∠B=∠C，
∴△BPD≌△CQP．
（2） 假设 △BPD≌△CQP，
∵vP≠vQ，
∴BP≠CQ，
又 ∵△BPD≌△CQP，∠B=∠C，
则 BP=CP=2 cm，BD=CQ=3 cm，
∴ 点 P 、点 Q 运动的时间 t=BP1=2（秒），
∴vQ=CQt=32=1.5cm/s．
（3） 设经过 x 秒后点 P 与点 Q 第一次相遇，
由题意，得 1.5x=x+2×6，解得 x=24，
∴ 点 P 共运动了 24×1=24cm．
∵4+6+6+4+4=24，
∴ 点 P 、点 Q 在 AC 边上相遇，
∴ 经过 24 秒点 P 与点 Q 第一次在边 AC 上相遇．