2018_2019学年南京市溧水县九上期末数学试卷

这是一份2018_2019学年南京市溧水县九上期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共6小题；共30分）
1. 下列函数中，y 是 x 的二次函数的是
A. y=2x−1B. y=1xC. y=1x2D. y=−x2+2x

2. 一元二次方程 x2+kx−3=0 的一个根是 x=1，则另一个根是
A. x=3B. x=−1C. x=−3D. x=−2

3. 一组数据：1，3，3，5，若添加一个数据 3，则下列统计量中发生变化的是
A. 平均数B. 中位数C. 众数D. 方差

4. 如图，正八边形 ABCDEFGH 中，∠EAG 大小为
A. 30∘B. 40∘C. 45∘D. 50∘

5. 如图，在 △ABC 中，点 D，E 分别在边 AB，AC 上，且 BD=2AD，CE=2AE，则下列结论：① △ABC∽△ADE；② DE∥BC；③ DE:BC=1:2；④ S△ABC=9S△ADE 中成立的有
A. 1 个B. 2 个C. 3 个D. 4 个

6. 如图，在平面直角坐标系 xOy 中，⊙P 与 x 轴相切于原点 O，平行于 y 轴的直线交 ⊙P 于 M，N 两点．若点 M 的坐标是 2,−1，则点 N 的坐标是
A. 2,−4B. 2,−4.5C. 2,−5D. 2,−5.5

二、填空题（共10小题；共50分）
7. 已知 ab=47，则 a−bb= ．

8. 如图，将 ∠AOB 放置在 5×5 的正方形网格中，则 tan∠AOB 的值是 ．

9. 二次函数 y=−2x−12+2 图象的顶点坐标是 ．

10. 如图，点 A，B，C 分别是 ⊙O 上的三点，已知 ∠AOB=50∘，则 ∠ACB 的大小是 ∘．

11. 一副扑克共 54 张牌（其中大王、小王各一张），洗匀后，从中任意抽取一张，抽出的牌是“王”的概率是 ．

12. 如图，圆锥的底面半径为 1 cm，高 SO 等于 22 cm，则侧面展开图扇形的圆心角为 ∘．

13. 如图，在 Rt△ABC 中，∠C=90∘，AC=4，BC=2，点 D，E，F 分别为 BC，AB，AC 上的点，若四边形 DEFC 为正方形，则它的边长为 ．

14. 如图，是二次函数 y=ax2+bx+c 的大致图象，则下列结论：① a0；③ c0 中，正确的有 ．（写上所有正确结论的序号）

15. 如图，已知图中的每个小方格都是边长为 1 的小正方形，每个小正方形的顶点称为格点．若 △ABC 与 △A1B1C1 是位似图形，且顶点都在格点上，则位似中心的坐标是 ．

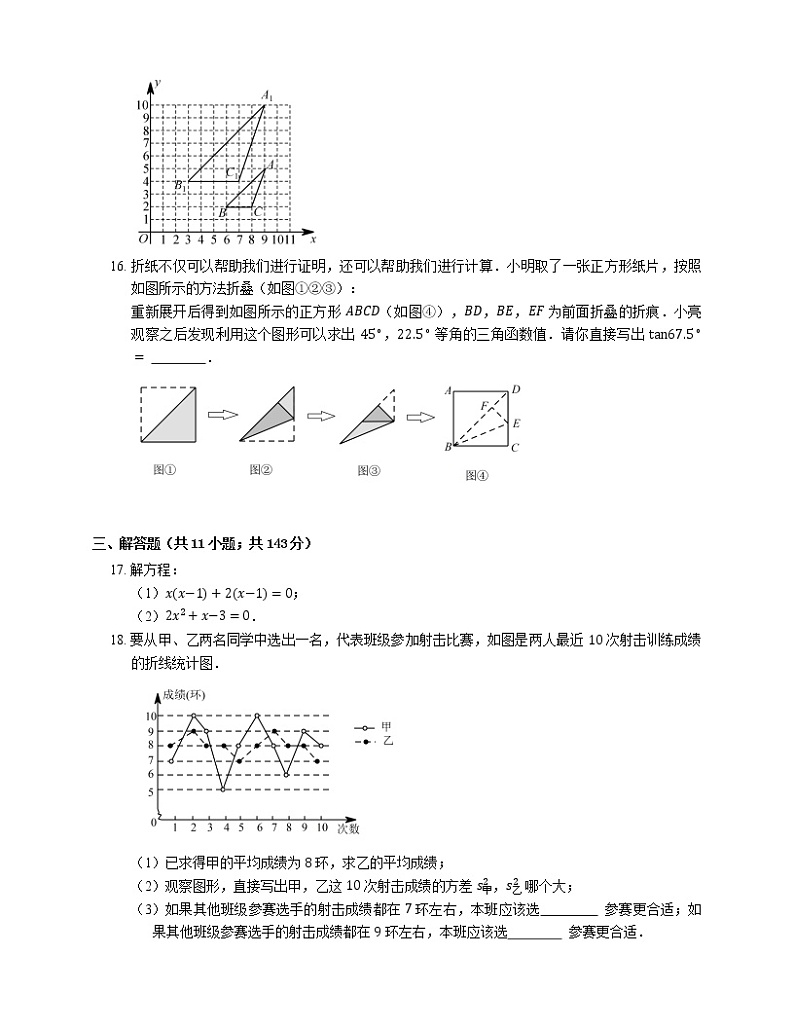
16. 折纸不仅可以帮助我们进行证明，还可以帮助我们进行计算．小明取了一张正方形纸片，按照如图所示的方法折叠（如图①②③）：
重新展开后得到如图所示的正方形 ABCD（如图④），BD，BE，EF 为前面折叠的折痕．小亮观察之后发现利用这个图形可以求出 45∘，22.5∘ 等角的三角函数值．请你直接写出 tan67.5∘= ．

三、解答题（共11小题；共143分）
17. 解方程：
（1）xx−1+2x−1=0；
（2）2x2+x−3=0．

18. 要从甲、乙两名同学中选出一名，代表班级参加射击比赛，如图是两人最近 10 次射击训练成绩的折线统计图．
（1）已求得甲的平均成绩为 8 环，求乙的平均成绩；
（2）观察图形，直接写出甲，乙这 10 次射击成绩的方差 s甲2，s乙2 哪个大；
（3）如果其他班级参赛选手的射击成绩都在 7 环左右，本班应该选 参赛更合适；如果其他班级参赛选手的射击成绩都在 9 环左右，本班应该选 参赛更合适．

19. 4 件同型号的产品中，有 1 件不合格品和 3 件合格品．
（1）从这 4 件产品中随机抽取 1 件进行检测，求抽到的是不合格品的概率；
（2）从这 4 件产品中随机抽取 2 件进行检测，求抽到的都是合格品的概率；
（3）在这 4 件产品中加入 x 件合格品后，进行如下试验：随机抽取 1 件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在 0.95，则可以推算出 x 的值大约是多少?

20. 在同一水平线 l 上的两根竹竿 AB，CD，它们在同一灯光下的影子分别为 BE，DF，如图所示：（竹竿都垂直于水平线 l）．
（1）根据灯光下的影子确定光源 S 的位置．
（2）画出影子为 GH 的竹竿 MG（用线段表示）．
（3）若在点 H 观测到光源 S 的仰角是 α，且 csα=45，GH=1.2 m，请求出竹竿 MG 的长度．

21. 如图，已知 ⊙O 的弦 AB，点 E，F 是 AB 上两点，AE=BF，OE，OF 分别交于 AB 于 C，D 两点，求证：AC=BD．

22. 如图，一堤坝的坡角 ∠ABC=60∘，坡面长度 AB=24 米（图为横截面）．为了使堤坝更加牢固，需要改变堤坝的坡面，为使得坡面的坡角 ∠ADB=45∘，则应将堤坝底端向外拓宽（BD）多少米?（结果精确到 0.1 米）（参考数据：2≈1.41，3≈1.73）

23. 如图，在平面直角坐标系 xOy 中，抛物线 y=x2−4x−5 与 x 轴交于 A，B 两点（点 A 在点 B 的左边），与 y 轴交于 C 点．
（1）求点 A，B，C 的坐标；
（2）点 x1,y1，x2,y2 在抛物线上，若 x10，所以④正确．
15. 9,0
【解析】连接 BB1，A1A，并延长，
由图可得交点坐标为 9,0．
16. 2+1
【解析】设 EC=x，
由折叠的性质可知，EF=EC=x，∠BFE=∠C=90∘，∠BDC=45∘，∠EBC=22.5∘，
∴DE=2EF=2x，∠BEC=67.5∘，
∴CD=2x+x，
由正方形的性质可知，BC=CD=2x+x，
∴tan67.5∘=tan∠BEC=BCCE=2+1．
第三部分
17. （1）
xx−1+2x−1=0.
分解因式得：
x−1x+2=0.
解得：
x1=1,x2=−2.
（2） 2x2+x−3=0，
这里 a=2，b=1，c=−3，
因为 Δ=b2−4ac=12−4×2×−3=1+24=25，
所以原方程有两个不等实数根，
所以 x=−1±254，
解得：x1=1，x2=−32．
18. （1） 乙的平均成绩是：8+9+8+8+7+8+9+8+8+7÷10=8（环）．
（2） 根据图象可知：甲的波动大于乙的波动，则 s甲2>s乙2．
（3） 乙；甲
【解析】如果其他班级参赛选手的射击成绩都在 7 环左右，本班应该选乙参赛更合适；
如果其他班级参赛选手的射击成绩都在 9 环左右，本班应该选甲参赛更合适．
19. （1） ∵4 件同型号的产品中，有 1 件不合格品，
∴P不合格品=14．
（2） 令不合格产品为甲，合格产品为乙、丙、丁，则随机抽 2 件的情况只有甲乙，甲丙，甲丁，乙丙，乙丁，丙丁，6 种情况．
合格的有 3 种情形，P抽到的都是合格品=36=12．
（3） ∵ 大量重复试验后发现，抽到合格品的频率稳定在 0.95，
∴ 抽到合格品的概率等于 0.95，
∴x+3x+4=0.95，
解得：x=16．
20. （1） 如图，点 S 即为所求，
（2） 如图，MG 即为所求．
（3） ∵csα=GHMH=45，GH=1.2，
∴MH=1.5，
在 Rt△MHG 中，∠MGH=90∘，
则 MG2=MH2−GH2=0.81，
则 MG=0.9 m，
答：竹杆 MG 的长度为 0.9 m．
21. 如图，连接 OA，OB，
∵ OA=OB，
∴ ∠A=∠B，
∵ AE=BF，
∴ ∠AOC=∠BOD，
在 △AOC 和 △BOD 中，
∠A=∠B,OA=OB,∠AOC=∠BOD.
∴ △AOC≌△BODASA，
∴ AC=BD．
22. 过点 A 作 AE⊥BC，垂足为点 E．
∵AB=24，∠ABC=60∘，
∴AE=AB⋅sin60∘=123，
BE=AB⋅cs60∘=12 米，
∵AE=123，∠ADB=45∘，
∴DE=123，
∴BD=123−12=123−1≈8.8 米．
答：应将堤坝底端向外拓宽（BD）8.8 米．
23. （1） 令 y=0，解得 x1=−1，x2=5，
所以 A−1,0，B5,0，
令 x=0，得 y=−5，
所以 C0,−5．
（2） >
【解析】如图，由抛物线开口向上，且对称轴为直线 x=2，
因为当 x1