初中数学青岛版九年级上册2.1 锐角三角比课时练习

这是一份初中数学青岛版九年级上册2.1 锐角三角比课时练习，共6页。试卷主要包含了1《锐角三角比》课时练习等内容，欢迎下载使用。

一、选择题
1.在Rt△ABC中，∠C=90°，AC=3，AB=4，那么csA的值是（ ）
A. B. C. D.
2.在Rt△ABC中，∠ABC=90°、tanA=，则sinA的值为（ ）
A. B. C. D.
3.把锐角△ABC各边都扩大2倍得△A′B′C′,那么∠A、∠A′余弦值关系是（ ）
A.csA=csA′ B.csA=2csA′ C.2csA=csA′ D.不确定的
4.在Rt△ABC中，∠C=90°，BC=1，那么AB的长为( )
A.sinA B.csA C. D.
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D．若AC=，BC=2,则sin∠ACD的值为（ ）

A. B. C. D.
6.如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,则tanA的值为（ ）

A.0.6 B.0.8 D.
7.如图，已知△ABC的三个顶点均在格点上，则csA的值为（ ）

A. B. C. D.
8.在Rt△ABC中，∠C=90°，若tanA=，则sinA=（ ）
A. B. C. D.
9.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为（ ）
A.1 B.0.6 C.
10.在Rt△ABC中,∠C=90°,AB=13,AC=12,则csA=( )
A. B. C. D.
二、填空题
11.如图,若点A的坐标为，则sin∠1= ．
12.如图,菱形ABCD的边长为10cm,DE⊥AB,sinA=，则这个菱形的面积= cm2．
13.如图，∠BAC位于6×6的方格纸中，其中A，B，C均为格点，则tan∠BAC= ．
14.已知在△ABC中，AB=AC=4，BC=6，那么csB=____________.
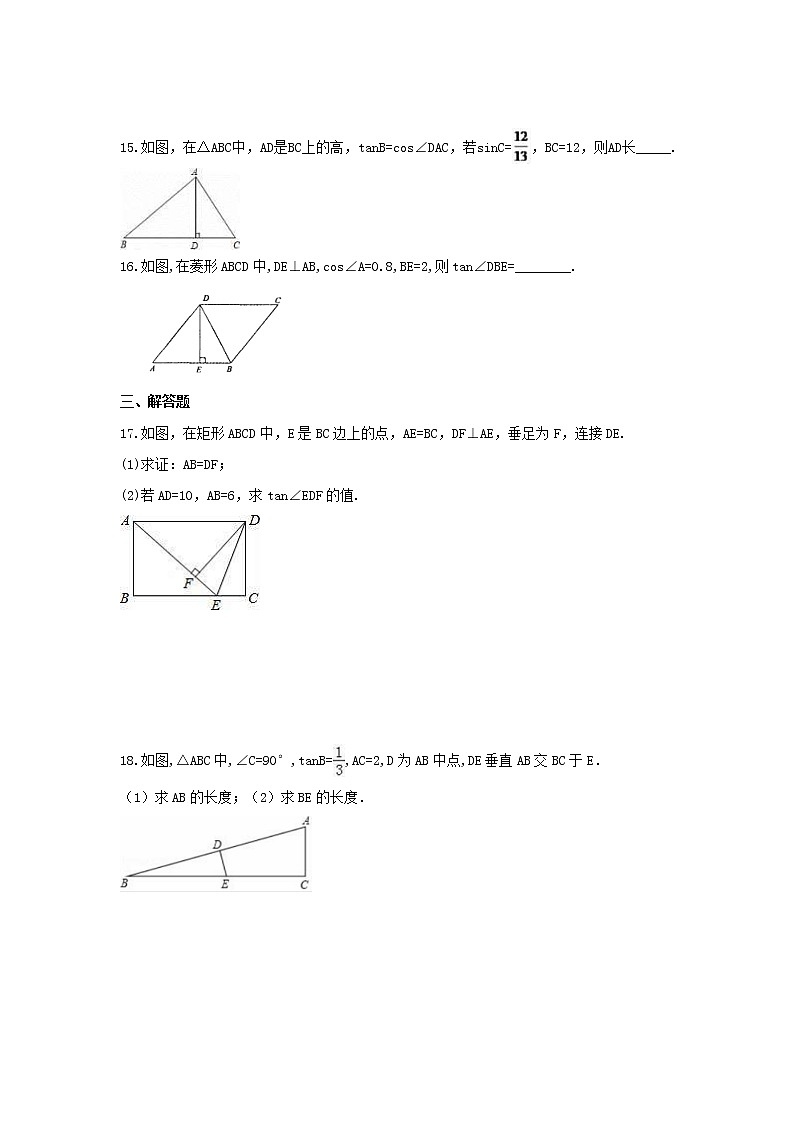
15.如图，在△ABC中，AD是BC上的高，tanB=cs∠DAC，若sinC=，BC=12，则AD长_____.

16.如图,在菱形ABCD中,DE⊥AB,cs∠A=0.8,BE=2,则tan∠DBE=________.

三、解答题
17.如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE.
(1)求证：AB=DF；
(2)若AD=10，AB=6，求tan∠EDF的值.
18.如图,△ABC中,∠C=90°,tanB=,AC=2,D为AB中点,DE垂直AB交BC于E．
（1）求AB的长度；（2）求BE的长度．
19.如图,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值．

20.如图，在△ABC中，CD⊥AB，垂足为D．若AB=12，CD=6，tanA=，求sinB+csB的值．

参考答案
1.B
2.A
3.A
4.D
5.A
6.D
7.D
8.D
9.D
10.C
11.答案为：．
12.菱形的面积=DE•AB=6×10=60（cm2）．
13.答案为：1.5．
14.答案为：0.75；
15.答案为8.
16.答案为：3
17. (1)证明：在矩形ABCD中，BC=AD，AD∥BC，∠B=90°，
∴∠DAF=∠AEB.
∵DF⊥AE，AE=BC，
∴∠AFD=90°，AE=AD.
∴△ABE≌△DFA；
∴AB=DF；
(2)解：由(1)知△ABE≌△DFA.∴AB=DF=6.
在Rt△ADF中，AF=，
∴EF=AE﹣AF=AD﹣AF=2.∴tan∠EDF==.
18.解：（1）∵∠C=90°，tanB=，AC=2，
∴BC=2AC=4，∴AB===2；
（2）∵D为AB中点，∴BD=AB=，
∵DE垂直AB交BC于E，tanB=，∴DE=BD=，
∴BE===．
19.提示：sin A＝，cs A＝，tan A=.
20.解：在Rt△ACD中，∵∠ADC=90°，
∴tanA===，∴AD=4，∴BD=AB﹣AD=12﹣4=8．
在Rt△BCD中，∵∠BDC=90°，BD=8，CD=6，∴BC==10，
∴sinB==，csB==，
∴sinB+csB=+=．故答案为：