初中数学华师大版九年级下册1. 圆的基本元素教学课件ppt

这是一份初中数学华师大版九年级下册1. 圆的基本元素教学课件ppt，共24页。PPT课件主要包含了学习目标，情景引入，圆的旋转定义，有关概念，知识精讲，半径相同圆心不同，圆心相同半径不同，确定一个圆的要素，满足什么条件的，有间隙吗等内容，欢迎下载使用。
认识圆，理解圆的本质属性.
认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，并了解它们之间的区别和联系.
初步了解点与圆的位置关系.
观察下列生活中的图片，找一找你所熟悉的图形.
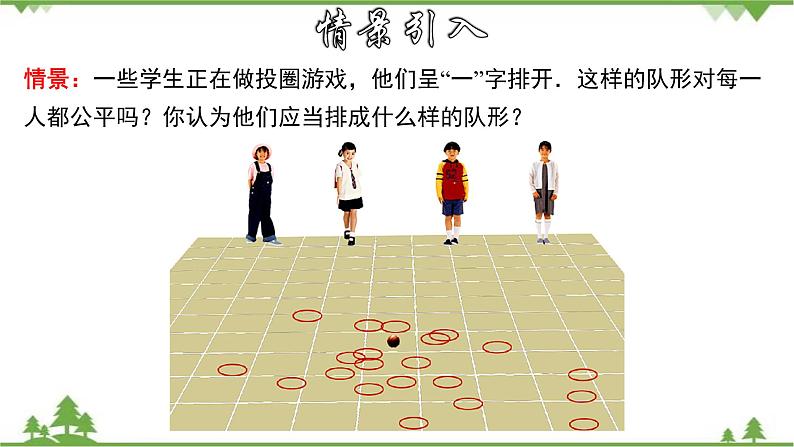
情景：一些学生正在做投圈游戏，他们呈“一”字排开．这样的队形对每一人都公平吗？你认为他们应当排成什么样的队形？
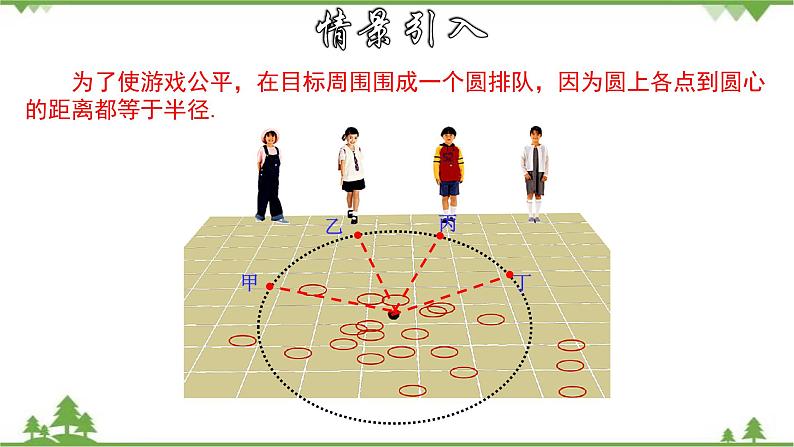
为了使游戏公平，在目标周围围成一个圆排队，因为圆上各点到圆心的距离都等于半径.
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点所形成的图形叫做圆．以点O为圆心的圆，记作“⊙O”，读作“圆O”.
固定的端点O叫做圆心，线段OA叫做半径，一般用r表示．
问题 观察画圆的过程，你能说出圆是如何画出来的吗？
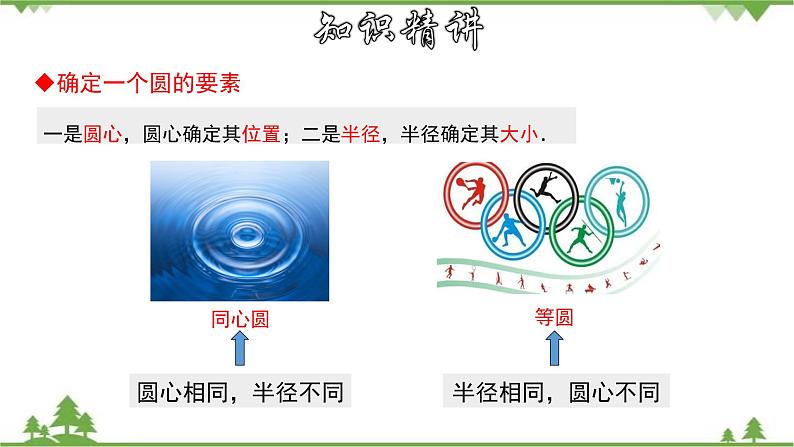
一是圆心，圆心确定其位置；二是半径，半径确定其大小．
圆可以看成到定点距离等于定长的所有点组成的.
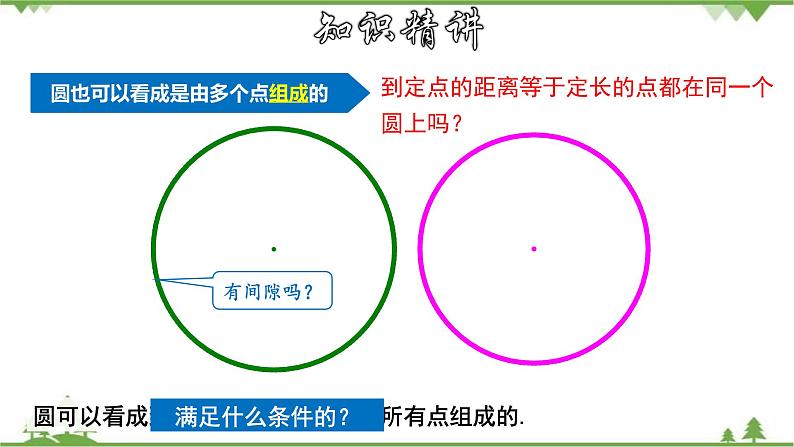
圆也可以看成是由多个点组成的
到定点的距离等于定长的点都在同一个圆上吗？
（1）圆上各点到定点（圆心O）的距离都等于________．（2）到定点的距离等于定长的点都在 ．
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合．
想一想：从画圆的过程可以看出什么呢？
例1 矩形ABCD的对角线AC、BD相交于O.求证：A、B、C、D在以O为圆心的同一圆上.
证明：∵四边形ABCD是矩形，
∴AO=OC，OB=OD.
又∵AC=BD，∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心，以OA为半径的圆上.
连接圆上任意两点的线段（如图中的AC）叫做弦.
经过圆心的弦（如图中的AB）叫做直径．
1.根据圆的定义，“圆”指的是“圆周”，而不是“圆面”．2.直径是圆中最长的弦.
连接OC,在△AOC中，根据三角形三边关系有AO+OC>AC,而AB=2OA,AO=OC,所以AB>AC.
探索：圆中最长的弦是什么？为什么？
【发现】直径是最长的弦
圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
能够重合的两个圆叫做等圆.
容易看出： 等圆是两个半径相等的圆.
在同圆或等圆中，能够互相重合的弧叫做等弧.
结论：等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图，如果AB和CD的拉直长度都是10cm，平移并调整小圆的位置，是否能使这两条弧完全重合？
想一想：长度相等的弧是等弧吗？
例2 如图.(1)请写出以点A为端点的优弧及劣弧;(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
（3）请任选一条弦，写出这条弦所对的弧.
例3 如图，MN是半圆O的直径，正方形ABCD的顶点A、D在半圆上，顶点B、C在直径MN上，求证：OB=OC.
连OA,OD即可，同圆的半径相等.
算一算：设在例3中，⊙O的半径为10，则正方形ABCD的边长为 .
变式：如图，在扇形MON中， ，半径MO=NO=10，,正方形ABCD的顶点B、C、D在半径上，顶点A在圆弧上，求正方形ABCD的边长.
设OC=x,则AB=BC=DC=OC=x
1.填空：（1）______是圆中最长的弦，它是______的2倍．（2）图中有 条直径， 条非直径的弦，圆中以A为一个端点的优弧有 条，劣弧有 条．
2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .
3.判断下列说法的正误，并说明理由或举反例.
(3)过圆心的线段是直径；
(4)过圆心的直线是直径；
(5)半圆是最长的弧；
(6)直径是最长的弦；
(7)长度相等的弧是等弧.