初中苏科版第3章 代数式综合与测试随堂练习题

这是一份初中苏科版第3章 代数式综合与测试随堂练习题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

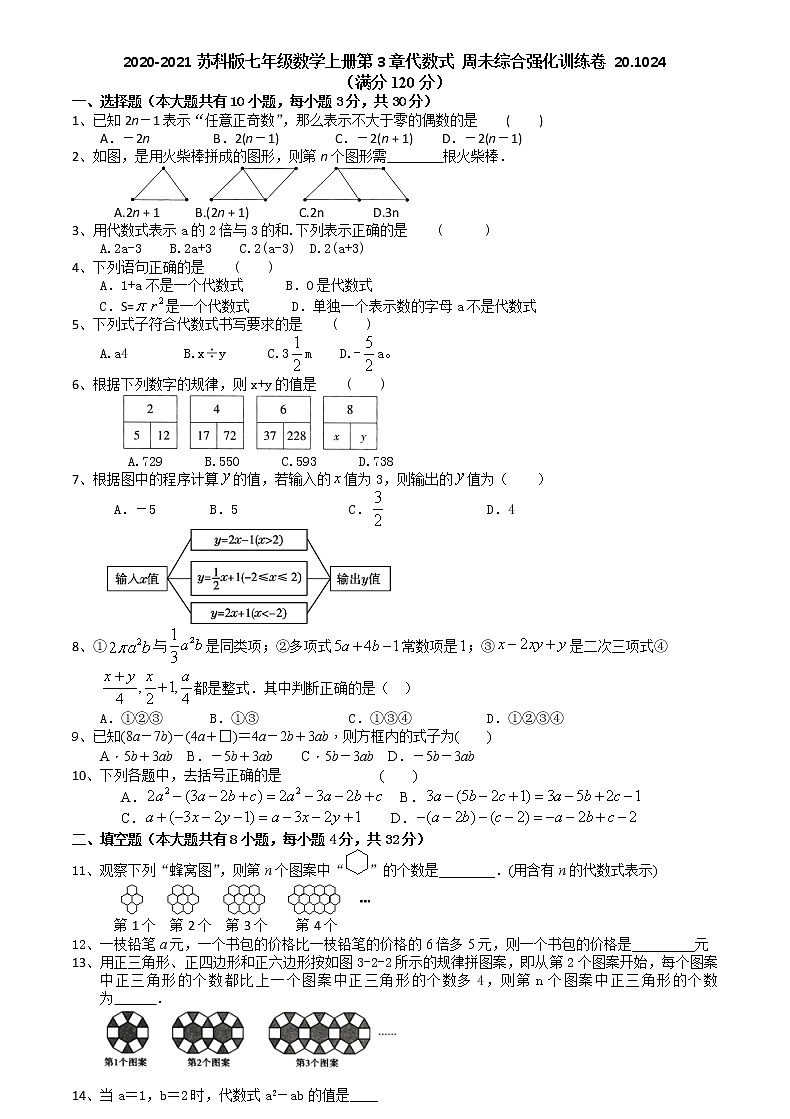
2020-2021苏科版七年级数学上册第3章代数式 周未综合强化训练卷 20.1024
（满分120分）
一、选择题（本大题共有10小题，每小题3分，共30分）
1、已知2n－1表示“任意正奇数”，那么表示不大于零的偶数的是 ( )
A．－2n B．2(n－1) C．－2(n + 1) D．－2(n－1)
2、如图，是用火柴棒拼成的图形，则第n个图形需 根火柴棒．

A.2n + 1 B.(2n + 1) C.2n D.3n
3、用代数式表示a的2倍与3的和.下列表示正确的是 ( )
A.2a-3 B.2a+3 C.2(a-3) D.2(a+3)
4、下列语句正确的是 ( )
A．1+a不是一个代数式 B．0是代数式
C．S=是一个代数式 D．单独一个表示数的字母a不是代数式
5、下列式子符合代数式书写要求的是 ( )
A.a4 B.x÷y C.3m D.-a。
6、根据下列数字的规律，则x+y的值是 ( )

A.729 B.550 C.593 D.738
7、根据图中的程序计算的值，若输入的值为3，则输出的值为（ ）
A．－5 B．5 C． D．4

8、①与是同类项；②多项式常数项是；③是二次三项式④都是整式．其中判断正确的是（ ）
A．①②③ B．①③ C．①③④ D．①②③④
9、已知(8a－7b)－(4a＋□)＝4a－2b＋3ab，则方框内的式子为(　　)
A．5b＋3ab B．－5b＋3ab C．5b－3ab D．－5b－3ab
10、下列各题中，去括号正确的是 ( )
A． B．
C． D．
二、填空题（本大题共有8小题，每小题4分，共32分）
11、观察下列“蜂窝图”，则第n个图案中“”的个数是________．(用含有n的代数式表示)

第1个 第2个 第3个 第4个
12、一枝铅笔a元，一个书包的价格比一枝铅笔的价格的6倍多5元，则一个书包的价格是_________元
13、用正三角形、正四边形和正六边形按如图3-2-2所示的规律拼图案，即从第2个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4，则第n个图案中正三角形的个数为 ．


14、当a＝1，b＝2时，代数式a2－ab的值是____
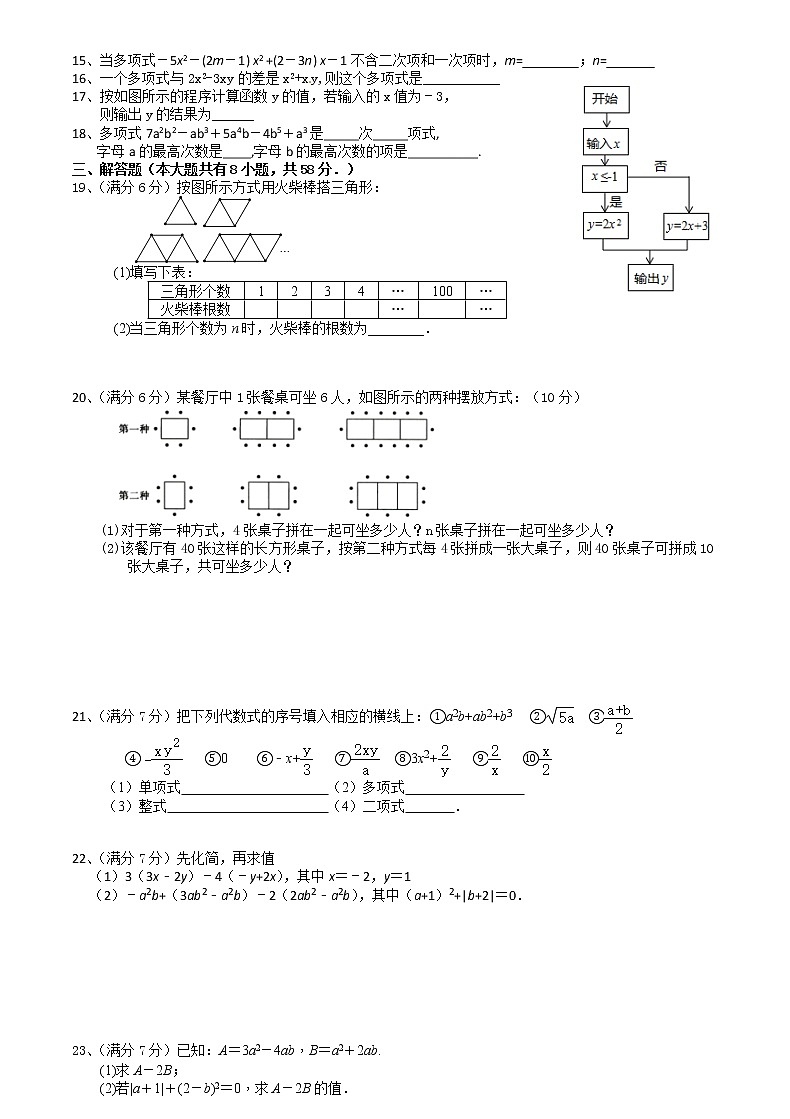
15、当多项式－5x2－(2m－1) x2 +(2－3n) x－1不含二次项和一次项时，m= ；n=
16、一个多项式与2x2-3xy的差是x2+xy,则这个多项式是___________
17、按如图所示的程序计算函数y的值，若输入的x值为﹣3，
则输出y的结果为______
18、多项式7a2b2－ab3＋5a4b－4b5＋a3是_____次_____项式,
字母a的最高次数是____,字母b的最高次数的项是__________.
三、解答题（本大题共有8小题，共58分．）
19、（满分6分）按图所示方式用火柴棒搭三角形：

(1)填写下表：
三角形个数
1
2
3
4
…
100
…
火柴棒根数




…

…
(2)当三角形个数为n时，火柴棒的根数为________．



20、（满分6分）某餐厅中1张餐桌可坐6人，如图所示的两种摆放方式：（10分）

(1)对于第一种方式，4张桌子拼在一起可坐多少人？n张桌子拼在一起可坐多少人？
(2)该餐厅有40张这样的长方形桌子，按第二种方式每4张拼成一张大桌子，则40张桌子可拼成10张大桌子，共可坐多少人？







21、（满分7分）把下列代数式的序号填入相应的横线上：①a2b+ab2+b3 ② ③
④ ⑤0 ⑥﹣x+ ⑦ ⑧3x2+ ⑨ ⑩
（1）单项式　 　 （2）多项式　 　
（3）整式　 　 （4）二项式　 　．


22、（满分7分）先化简，再求值
（1）3（3x﹣2y）﹣4（﹣y+2x），其中x＝﹣2，y＝1
（2）﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中（a+1）2+|b+2|＝0．








23、（满分7分）已知：A＝3a2－4ab，B＝a2＋2ab.
(1)求A－2B；
(2)若|a＋1|＋(2－b)2＝0，求A－2B的值．









24、（满分7分）在市南区某住房小区建设中，为了提高业主的宜居环境，某小区因地制宜规划修建一个广场（图中阴影部分）．
（1）用含m、n的代数式表示该广场的周长C；
（2）用含m、n的代数式表示该广场的面积S；
（3）若m、n满足（m﹣6）2+|n﹣8|＝0，求出该广场的周长和面积．



25、（满分9分）某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元，厂方在开展促销活动期间，向客户提供了两种优惠方案：
方案①：买一套西装送一条领带； 方案②：西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x(x>20)条．
(1)若该客户按方案①购买，需付款_____________元(用含x 的代数式表示)；若该客户按方案②购买，需付款________________元(用含x的代数式表示)．
(2)若x＝30，通过计算说明此时按哪种方案购买较为合算．











26、（满分9分）已知多项式(2x2＋ax－y＋6)－(2bx2－3x＋5y－1)．
(1)若多项式的值与字母x的取值无关，求a，b的值；
(2)在(1)的条件下，先化简多项式3(a2－ab＋b2)－(3a2＋ab＋b2)，再求它的值．












2020-2021苏科版七年级数学上册第3章代数式 周未综合强化训练卷（答案）20.10.24
（满分120分）
一、选择题（本大题共有10小题，每小题3分，共30分）
1、已知2n－1表示“任意正奇数”，那么表示不大于零的偶数的是 ( D )
A．－2n B．2(n－1) C．－2(n + 1) D．－2(n－1)
2、如图，是用火柴棒拼成的图形，则第n个图形需 B 根火柴棒．

A.2n + 1 B.(2n + 1) C.2n D.3n
3、用代数式表示a的2倍与3的和.下列表示正确的是 ( B )
A.2a-3 B.2a+3 C.2(a-3) D.2(a+3)
4、下列语句正确的是 ( B )
A．1+a不是一个代数式 B．0是代数式
C．S=是一个代数式 D．单独一个表示数的字母a不是代数式
5、下列式子符合代数式书写要求的是 ( D )
A.a4 B.x÷y C.3m D.-a。
6、根据下列数字的规律，则x+y的值是 ( C )

A.729 B.550 C.593 D.738
解析：∵5= +1，12= 5×2+2；17= 4+1，72= 17×4+4；37= 6+1，228= 37x6+6，
∴x=8+1=65，y=65×8+8=528，x+y= 65+528= 593.故选C．
7、根据图中的程序计算的值，若输入的值为3，则输出的值为（ B ）
A．－5 B．5 C． D．4

8、①与是同类项；②多项式常数项是；③是二次三项式④都是整式．其中判断正确的是（C ）
A．①②③ B．①③ C．①③④ D．①②③④
9、已知(8a－7b)－(4a＋□)＝4a－2b＋3ab，则方框内的式子为(　　)
A．5b＋3ab B．－5b＋3ab C．5b－3ab D．－5b－3ab
[解析] 4a＋□＝(8a－7b)－(4a－2b＋3ab)＝8a－7b－4a＋2b－3ab＝4a－5b－3ab.
故□＝－5b－3ab. D　
10、下列各题中，去括号正确的是 ( B )
A． B．
C． D．
二、填空题（本大题共有8小题，每小题4分，共32分）
11、观察下列“蜂窝图”，则第n个图案中“”的个数是__3n＋1______．(用含有n的代数式表示)

第1个 第2个 第3个 第4个
12、一枝铅笔a元，一个书包的价格比一枝铅笔的价格的6倍多5元，则一个书包的价格是__(6a＋5)__元
13、用正三角形、正四边形和正六边形按如图3-2-2所示的规律拼图案，即从第2个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4，则第n个图案中正三角形的个数为 ．

解析：第1个图案中正三角形的个数为6=2+4；第2个图案中正三角形的个数为2+4+4= 2+2×4；
第3个图案中正三角形的个数为2+2×4+4=2+3×4；……；
第n个图案中正三角形的个数为2+（n-1）×4+4= 2+4n= 4n+2.
14、当a＝1，b＝2时，代数式a2－ab的值是__－1 ___
15、当多项式－5x2－(2m－1) x2 +(2－3n) x－1不含二次项和一次项时，m= m=－2 ；n= n=
16、一个多项式与2x2-3xy的差是x2+xy,则这个多项式是_____3x2-2xy ______
17、按如图所示的程序计算函数y的值，若输入的x值为﹣3，
则输出y的结果为___18 ___
18、多项式7a2b2－ab3＋5a4b－4b5＋a3是_____次_____项式,
字母a的最高次数是____,字母b的最高次数的项是__________.
答案：五,五,4,－4b2

三、解答题（本大题共有8小题，共58分．）
19、（满分6分）按图所示方式用火柴棒搭三角形：

(1)填写下表：
三角形个数
1
2
3
4
…
100
…
火柴棒根数




…

…
(2)当三角形个数为n时，火柴棒的根数为________．

解：(1)填写表格如下：

三角形个数
1
2
3
4
…
100
…
火柴棒根数
3
5
7
9
…
201
…
(2)当三角形个数为n时，火柴棒的根数为2n＋1.

20、（满分6分）某餐厅中1张餐桌可坐6人，如图所示的两种摆放方式：（10分）

(1)对于第一种方式，4张桌子拼在一起可坐多少人？n张桌子拼在一起可坐多少人？
(2)该餐厅有40张这样的长方形桌子，按第二种方式每4张拼成一张大桌子，则40张桌子可拼成10张大桌子，共可坐多少人？
解析(1)一张桌子可坐6人，每增加一张桌子可多坐4人，所以4张桌子拼在一起可以坐18人，n张桌子拼在一起可坐6+4(n-1)=(4n+2)人．
(2)一张桌子可坐6人，每增加一张桌子可多坐2人，所以4张桌子拼成的大桌子面以坐12人，所以10张大桌子共可坐10x12= 120(人)．

21、（满分7分）把下列代数式的序号填入相应的横线上：①a2b+ab2+b3 ② ③
④ ⑤0 ⑥﹣x+ ⑦ ⑧3x2+ ⑨ ⑩
（1）单项式　 　 （2）多项式　 　
（3）整式　 　 （4）二项式　 　．
解：（1）单项式 ④⑤⑩ （2）多项式 ①③⑥
（3）整式 ①③④⑤⑥⑩ （4）二项式 ③⑥．


22、（满分7分）先化简，再求值
（1）3（3x﹣2y）﹣4（﹣y+2x），其中x＝﹣2，y＝1
（2）﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中（a+1）2+|b+2|＝0．
【解析】解：（1）原式＝9x﹣6y+4y﹣8x＝x﹣2y，
当x＝﹣2，y＝1时，原式＝﹣2﹣2＝﹣4；
（2）原式＝﹣a2b+3ab2﹣a2b﹣4ab2+2a2b＝﹣ab2 ，
∵（a+1）2+|b+2|＝0，∴a＝﹣1，b＝﹣2，
则原式＝4．

23、（满分7分）已知：A＝3a2－4ab，B＝a2＋2ab.
(1)求A－2B；
(2)若|a＋1|＋(2－b)2＝0，求A－2B的值．
解：(1)A－2B＝(3a2－4ab)－2(a2＋2ab)＝3a2－4ab－2a2－4ab＝a2－8ab.
(2)因为|a＋1|＋(2－b)2＝0，得a＝－1，b＝2.
所以A－2B＝a2－8ab＝(－1)2－8×(－1)×2＝1＋16＝17.

24、（满分7分）在市南区某住房小区建设中，为了提高业主的宜居环境，某小区因地制宜规划修建一个广场（图中阴影部分）．
（1）用含m、n的代数式表示该广场的周长C；
（2）用含m、n的代数式表示该广场的面积S；
（3）若m、n满足（m﹣6）2+|n﹣8|＝0，求出该广场的周长和面积．

解：（1）C＝6m+4n；
（2）S＝2m×2n﹣m（2n﹣n﹣0.5n）＝4mn﹣0.5mn ＝3.5mn；
（3）由题意得m﹣6＝0，n﹣8＝0， ∴m＝6，n＝8，
代入，可得原式＝3.5×6×8＝168．

25、（满分9分）某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元，厂方在开展促销活动期间，向客户提供了两种优惠方案：
方案①：买一套西装送一条领带； 方案②：西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x(x>20)条．
(1)若该客户按方案①购买，需付款_____________元(用含x 的代数式表示)；若该客户按方案②购买，需付款________________元(用含x的代数式表示)．
(2)若x＝30，通过计算说明此时按哪种方案购买较为合算．
解：(1)(40x＋3200)， (36x＋3600)
(2)当x＝30时，40x＋3200＝40×30＋3200＝4400，即方案①需付款4400元；
36x＋3600＝36×30＋3600＝4680， 即方案②需付款4680元．
因为4400＜4680，所以此时按方案①购买较为合算．

26、（满分9分）已知多项式(2x2＋ax－y＋6)－(2bx2－3x＋5y－1)．
(1)若多项式的值与字母x的取值无关，求a，b的值；
(2)在(1)的条件下，先化简多项式3(a2－ab＋b2)－(3a2＋ab＋b2)，再求它的值．
解：(1)原式＝2x2＋ax－y＋6－2bx2＋3x－5y＋1＝(2－2b)x2＋(a＋3)x－6y＋7，
由结果与x的取值无关，可知a＋3＝0，2－2b＝0，
解得a＝－3，b＝1.
(2)原式＝3a2－3ab＋3b2－3a2－ab－b2＝－4ab＋2b2.
当a＝－3，b＝1时，原式＝－4×(－3)×1＋2×12＝12＋2＝14.