初中数学人教版九年级上册22.1.1 二次函数教案设计

这是一份初中数学人教版九年级上册22.1.1 二次函数教案设计，共3页。
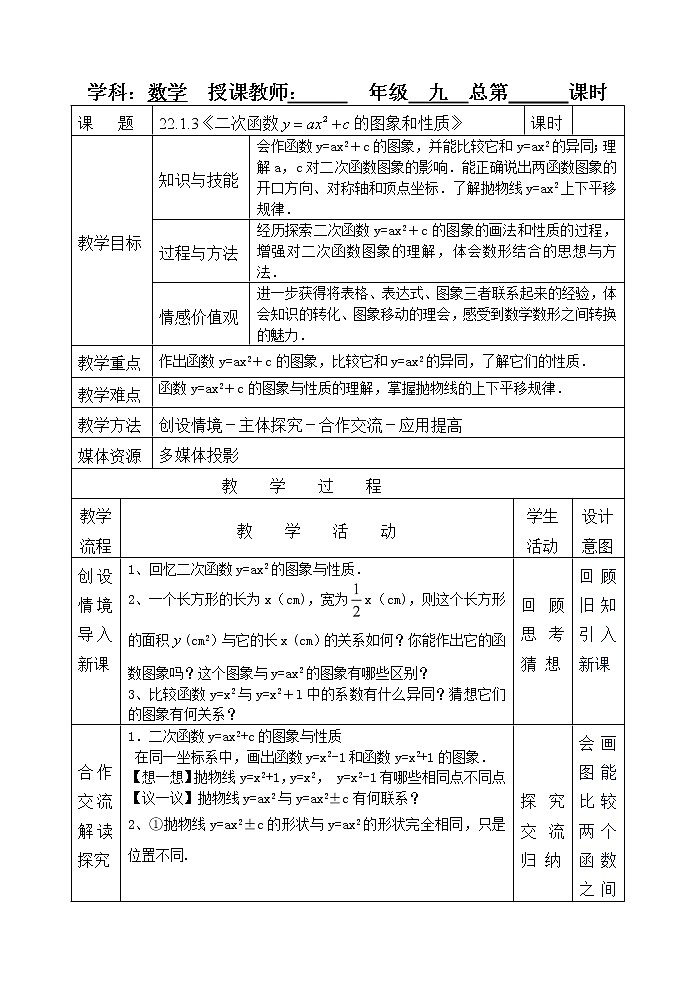
课 题
22.1.3《二次函数的图象和性质》
课时
教学目标
知识与技能
会作函数y=ax2＋c的图象，并能比较它和y=ax2的异同；理解a，c对二次函数图象的影响．能正确说出两函数图象的开口方向、对称轴和顶点坐标．了解抛物线y=ax2上下平移规律．
过程与方法
经历探索二次函数y=ax2＋c的图象的画法和性质的过程，增强对二次函数图象的理解，体会数形结合的思想与方法．
情感价值观
进一步获得将表格、表达式、图象三者联系起来的经验，体会知识的转化、图象移动的理会，感受到数学数形之间转换的魅力．
教学重点
作出函数y=ax2＋c的图象，比较它和y=ax2的异同，了解它们的性质．
教学难点
函数y=ax2＋c的图象与性质的理解，掌握抛物线的上下平移规律．
教学方法
创设情境－主体探究－合作交流－应用提高
媒体资源
多媒体投影
教 学 过 程
教学流程
教 学 活 动
学生活动
设计意图
创设情境 导入新课
1、回忆二次函数y=ax2的图象与性质．
2、一个长方形的长为x（cm)，宽为x（cm)，则这个长方形的面积(cm2）与它的长x (cm）的关系如何？你能作出它的函数图象吗？这个图象与y=ax2的图象有哪些区别？
3、比较函数y=x2与y=x2＋l中的系数有什么异同？猜想它们的图象有何关系？
回顾思考猜 想
回顾旧知引入新课
合作交流 解读探究
1．二次函数y=ax2+c的图象与性质
在同一坐标系中，画出函数y=x2-1和函数y=x2+1的图象．
【想一想】抛物线y=x2+1，y=x2， y=x2-1有哪些相同点不同点
【议一议】抛物线y=ax2与y=ax2±c有何联系？
2、①抛物线y=ax2±c的形状与y=ax2的形状完全相同，只是位置不同.
②抛物线y=ax2y=ax2+c. y=ax2y=ax2-c
探究交流归 纳
会画图能比较两个函数之间关系
巩固知识
1、在同一坐标系中画：、、的图象；并指出相同点不同点。
2、P33页：练习题。
动手解答
巩固新知
应用迁移 巩固提高
1、函数y=ax2+c的图象特征与性质的运用
抛物线y=ax2+c与y=-5x2的形状大小，开口方向都相同，且顶点坐标是(0,3),则其表达式为 y=-5x2+3 ，它是由抛物线y=-5x2向 上 平移 3 个单位得到的.
2、求二次函数的解析式
（1）若抛物线y=ax2+c经过点（-1，2），（0，4），求该抛物线的解析式
（2）已知抛物线y=ax2+c向下平移2个单位后，所得抛物线为y=-3x2+2.试求a、c的值
讨论分析解答
灵活应用新知
课堂小结
1、本节所学知识是函数y=ax2+c的图象与性质以及抛物线y=ax2上下平移规律.
2、所学的思想方法图象法、数形结合的思想.
作业布置
1、P41页：习题22.1：第5（1）
2、补充练习：
（1）.抛物线y=-2x2-5的开口方向 向下 ，对称轴是 y 轴 ，顶点坐标 （0，-5）.
（2）. 抛物线y=ax2+c与y=3x2的形状相同，且其顶点坐标为（0，1），则其表达式为 y=3x2+1或y=-3x2+1.
（3）. 抛物线y=-+7向 下 平移 10 个单位后得到抛物线y=--3
（4）. 下列各组抛物线中能够互相平移而彼此得到对方的是（ D ）
A.y=2x2与y=3x2 B. y=+2与y=2x2+
C.y=2x2与y=x2+2 D.y=x2+2与y=-x2-2，
教学反思
灵活应用函数y=ax2+c的图象与性质以及抛物线y=ax2上下平移规律复习解决问题.