2018_2019学年天津市南开区九上期末考试数学试卷

这是一份2018_2019学年天津市南开区九上期末考试数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列事件中是不可能事件的是
A. 每天早晨太阳从东方升起B. 公鸡下蛋
C. 下雨时打雷D. 体育运动中肌肉拉伤

2. 下列图标中，既是轴对称图形，又是中心对称图形的是
A. B.
C. D.

3. 若关于 x 的一元二次方程 x2+4x+2k=0 无实数根，则 k 值可以是
A. 3B. 2C. 0D. −5

4. 如果点 −1,y1，B1,y2，C2,y3 是反比例函数 y=1x 图象上的三个点，则下列结论正确的是
A. y1>y3>y2B. y3>y2>y1C. y2>y1>y3D. y3>y1>y2

5. 如图，在平面直角坐标系 xOy 中，以原点为位似中心，线段 AB 与线段 AʹBʹ 是位似图形，若 A−1,2，B−1,0，Aʹ−2,4，则 Bʹ 的坐标为
A. 2,4B. 1,0C. −2,2D. −2,0

6. 如图，点 A，B，C 在 ⊙O 上，∠ABC=29∘，过点 C 作 ⊙O 的切线交 OA 的延长线于点 D，则 ∠D 的大小为
A. 29∘B. 32∘C. 42∘D. 58∘

7. 一个扇形的圆心角是 120∘，面积为 3π cm2，那么这个扇形的半径是
A. 1 cmB. 3 cmC. 6 cmD. 9 cm

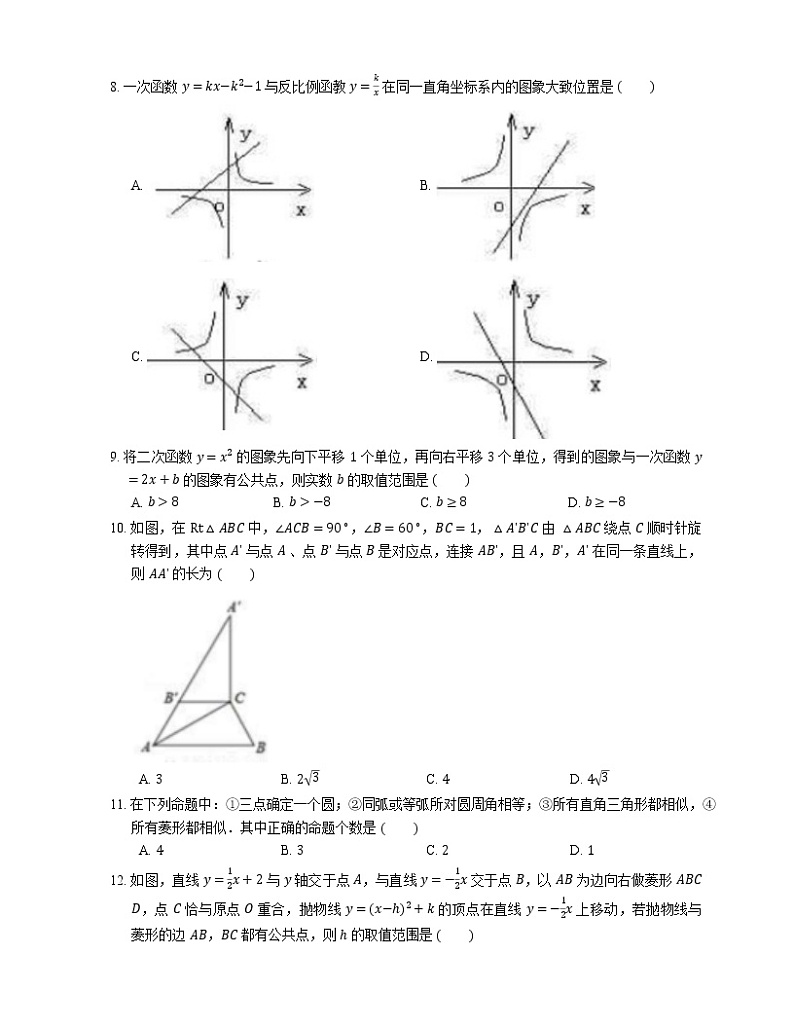
8. 一次函数 y=kx−k2−1 与反比例函教 y=kx 在同一直角坐标系内的图象大致位置是
A. B.
C. D.

9. 将二次函数 y=x2 的图象先向下平移 1 个单位，再向右平移 3 个单位，得到的图象与一次函数 y=2x+b 的图象有公共点，则实数 b 的取值范围是
A. b>8B. b>−8C. b≥8D. b≥−8

10. 如图，在 Rt△ABC 中，∠ACB=90∘，∠B=60∘，BC=1，△AʹBʹC 由 △ABC 绕点 C 顺时针旋转得到，其中点 Aʹ 与点 A 、点 Bʹ 与点 B 是对应点，连接 ABʹ，且 A，Bʹ，Aʹ 在同一条直线上，则 AAʹ 的长为
A. 3B. 23C. 4D. 43

11. 在下列命题中：①三点确定一个圆；②同弧或等弧所对圆周角相等；③所有直角三角形都相似，④所有菱形都相似．其中正确的命题个数是
A. 4B. 3C. 2D. 1

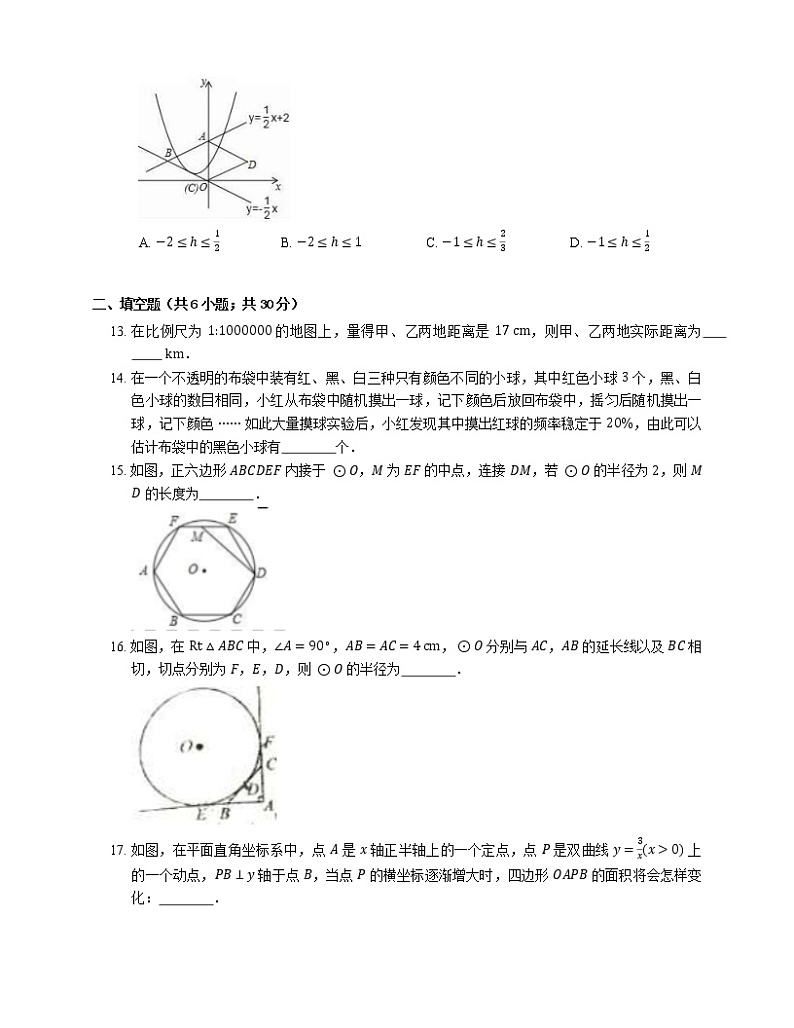
12. 如图，直线 y=12x+2 与 y 轴交于点 A，与直线 y=−12x 交于点 B，以 AB 为边向右做菱形 ABCD，点 C 恰与原点 O 重合，抛物线 y=x−h2+k 的顶点在直线 y=−12x 上移动，若抛物线与菱形的边 AB，BC 都有公共点，则 h 的取值范围是
A. −2≤h≤12B. −2≤h≤1C. −1≤h≤23D. −1≤h≤12

二、填空题（共6小题；共30分）
13. 在比例尺为 1:1000000 的地图上，量得甲、乙两地距离是 17 cm，则甲、乙两地实际距离为 km．

14. 在一个不透明的布袋中装有红、黑、白三种只有颜色不同的小球，其中红色小球 3 个，黑、白色小球的数目相同，小红从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后随机摸出一球，记下颜色 ⋯⋯ 如此大量摸球实验后，小红发现其中摸出红球的频率稳定于 20%，由此可以估计布袋中的黑色小球有 个．

15. 如图，正六边形 ABCDEF 内接于 ⊙O，M 为 EF 的中点，连接 DM，若 ⊙O 的半径为 2，则 MD 的长度为 ．

16. 如图，在 Rt△ABC 中，∠A=90∘，AB=AC=4 cm，⊙O 分别与 AC，AB 的延长线以及 BC 相切，切点分别为 F，E，D，则 ⊙O 的半径为 ．

17. 如图，在平面直角坐标系中，点 A 是 x 轴正半轴上的一个定点，点 P 是双曲线 y=3xx>0 上的一个动点，PB⊥y 轴于点 B，当点 P 的横坐标逐渐增大时，四边形 OAPB 的面积将会怎样变化： ．

18. 如图，在正方形 ABCD 中，△BPC 是等边三角形，BP，CP 的延长线分别交 AD 于点 E，F，连接 BD，DP，BD 与 CF 相交于点 H，给出下列结论：
① BB=2AE；
② △DFP∽△BPH；
③ △PFD∽△PDB；
④ S△BPDS正方形ABCD=3−14．
其中正确的是 （只需填写序号）．

三、解答题（共7小题；共91分）
19. 某校高一年级今年计划招四个班的新生，并采取随机摇号的方法分班．小明和小红既是该校的高一新生，又是好朋友，求小明和小红分在同一个班的概率（列出表格或画出树形图）．

20. 如图，一次函数 y=x+m 的图象与反比例函数 y=kx 的图象交于 A，B 两点，且与 x 轴交于点 C，点 A 的坐标为 2,1．
（1）求 m 及 k 的值；
（2）求点 C 的坐标，并结合图象写出当 0
21. 如图，已知左、右并排的两棵树高分别是 AB=8 m，CD=12 m，两树的根部的距离 BD=5 m，小明眼睛离地面的高度 EF 为 1.6 m，他沿着正对这两棵树的一条水平直路从左向右前进，当他与左边较低的树的距离小于多少时，就不能看到右边较高的树的顶端点 C?

22. 如图 1，在 △ABC 中，点 D 在边 BC 上，∠ABC:∠ACB:∠ADB=1:2:3，⊙O 是 △ABD 的外接圆．
（1）求证：AC 是 ⊙O 的切线；
（2）当 BD 是 ⊙O 的直径时（如图 2），求 ∠CAD 的度数．

23. 进入冬季，我市多次出现雾霾天气，商场根据市民健康需要，代理销售一种防尘口罩，进货价为 20 元/包，经市场调研发现：销售单价为 30 元/包时，每周可售出 100 包，每涨价 1 元，就少售出 5 包，若供货厂家规定市场价不得低于 30 元/包，且商场每周要完成不少于 150 包的销售任务．
（1）试确定周销售量 y（包）与售价 x（元/包）之间的函数关系式；
（2）试确定商场每周销售这种防尘口罩所获得的利润 w（元）与售价 x（元/包）之间的函数关系式，并直接写出售价 x 的范围；
（3）当售价 x（元/包）定为多少元时，商场每周销售这种防尘口罩所获得的利润 w（元）最大?最大利润是多少?

24. 如图 1，在平面直角坐标系，O 为坐标原点，将 △AOB 绕点 O 顺时针旋转得 △AʹOBʹ，点 A−1,0．
（1）当旋转角为 60∘ 时，点 Aʹ 恰好落在 AB 边上，则 B 点的坐标为 ．
（2）在（1）的条件下，设 △ABʹO 的面积为 S1，△BAʹO 的面积为 S2，S1 与 S2 有何关系?为什么?
（3）若将 △AOB 绕点 O 顺时针旋转到如图 2 所示的位置，S1 与 S2 的关系发生变化了吗?证明你的判断．

25. 在平面直角坐标系 xOy 中，抛物线 y=−x2+mx+n 与 x 轴交于点 A，B（A 在 B 的左侧）．
（1）抛物线的对称轴为直线 x=−3，AB=4．求抛物线的表达式．
（2）平移（1）中的抛物线，使平移后的抛物线经过点 O，且与 x 正半轴交于点 C，记平移后的抛物线顶点为 P，若 △OCP 是等腰直角三角形，求点 P 的坐标．
（3）当 m=4 时，抛物线上有两点 Mx1,y1 和 Nx2,y2，若 x1<2，x2>2，x1+x2>4，试判断 y1 与 y2 的大小，并说明理由．
答案
第一部分
1. B
2. A
3. A
4. A
5. D
6. B
7. B
8. C
9. D
10. A
11. D
12. A
第二部分
13. 170
14. 6
15. 7
16. 4+22
17. 变小
18. ①②④
第三部分
19.
∴ 小明和小红分在同一个班的概率为 416=14．
20. （1） ∵ A2,1 在 y=x+m 上，
∴ 1=2+m，
∴ m=−1．
∵ A2,1 在 y=kx 上，
∴ 1=k2，
∴ k=2；
（2） 由图象可知，当 021. 过 E 作 EC⊥CD 于 G，交 AB 于 H，
∵EFDC，HBDG 都是矩形，EF=16，AB=8，CD=12，BD=5，
∴AH=6.4，CG=10.4，HG=5，EH=FB，
∵AB∥CD，
∴EHEG=AHCG，
∴EHEH+5=6.410.4，
解得：EH=8，
∴FB=8（米）．
答：当他与左边较低的树的距离小于 8 米时，就不能看到右边最高树的顶端 C．
22. （1） 连接 AO，延长 AO 交 ⊙O 于点 E，则 AE 为 ⊙O 的直径，连接 DE，如图所示，
∵∠ABC:∠ACB:∠ADB=1:2:3，∠ADB=∠ACB+∠CAD，
∴∠ABC=∠CAD，
∵AE 为 ⊙O 的直径，
∴∠ADE=90∘，
∴∠EAD=90∘−∠AED，
∵∠AED=∠ABD，
∴∠AED=∠ABC=∠CAD，
∴∠EAD=90∘−∠CAD，
即 ∠EAD+∠CAD=90∘，
∴EA⊥AC，
∴AC 是 ⊙O 的切线．
（2） ∵BD 是 ⊙O 的直径，
∴∠BAD=90∘，
∴∠ABC+∠ADB=90∘，
∵∠ABC:∠ACB:∠ADB=1:2:3，
∴4∠ABC=90∘，
∴∠ABC=22.5∘，
由（1）知，∠ABC=∠CAD，
∴∠CAD=22.5∘．
23. （1） y=200−5x−30=200−5x+150=350−5x.
∴y=−5x+35030≤x≤40．
（2） 30≤x≤40．
【解析】w=x−20−5x+350=−5x−20x−70=−5x2−90x+1400=−5x2+450x−700030≤x≤40.
（3） w=−5x−452+3125，
∵30≤x≤40，
∴ 当 x=40 时，w 有最大值，
此时 w=40−20−5×40+350，
w=20×150，
w=3000．
答：当售价为 40 元/包时，商场获得利润最大，最大为 3000 元．
24. （1） 0,3
（2） ∵ 旋转，
∴OA=OAʹ，∠AOAʹ=60∘，
∴OA=OAʹ=AAʹ=1，∠BAO=60∘．
∴∠ABO=30∘．
∴AB=2．
∵AAʹ=1，
∴BAʹ=1．
设 BO 与 AAʹ 交于 D，
在 Rt△BAʹD 中，AʹD=12，∠BAʹD=60∘，
∴∠OAʹB=60∘．
∴AʹBʹ∥AO．
∴yBʹ=32．
∴S△ABʹO=12AO⋅∣yBʹ∣=12×1×32=34，
S△BAʹO=12⋅BO⋅AʹD=12⋅3×12=34．
∴S1=S△ABʹO=S△BAʹO=S2．
（3） S1=S2．
做 AʹM⊥BO 于 M，AN⊥BʹO 于 N．
∵∠AON+∠NOB=90∘，∠AʹOM+∠NOB=90∘，
∴∠AON=∠AʹOM．
在 △AON 与 △AʹOM 中，∠AON=∠AʹOM,∠OMAʹ=∠ONA=90∘,OA=OAʹ,
∴△AON≌△AʹOM．
∴AN=AʹM．
∵ 旋转，
∴OB=OBʹ．
∴S1=12⋅OBʹ⋅AN=12⋅OB⋅AM=S2．
25. （1） ∵ 对称轴为 x=−3，AB=4，
∴ A−5,0，B−1,0，
∴y=−x+5x+1，
y=−x2+6x+5，
y=−x2−6x−5．
（2） ∵ 平移后与 x 轴正半轴交于 C，
∴ 设平移后的解析式为 y=−x2+bxb>0，
∴ y=−x−b22+b24，
∴ Pb2,b24，
∵ △OCP 为等腰直角三角形，
∴ b2=b24，
解得：b=0 或 b=2，
∵ b>0，
∴ b=2，
∴ P1,1．
（3） 当 m=4 时，抛物线 y=−x2+4x+n．
∴ 对称轴为 x=2，
∵ x1<2，x2>2，
∴ M，N 分别在对称轴两侧，
∵ x1+x2>4，
∴ x1−2>2−x2，
∴ 2−x1 ∴ M 比 N 距离对称轴近．
∵ y=−x2+4x+n 开口向下，
∴ 距离对称轴越近，出数值越大．
∴ y1>y2．