2018_2019学年广东省佛山市三水区八下期末数学试卷

这是一份2018_2019学年广东省佛山市三水区八下期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 下列交通标志既是中心对称图形又是轴对称图形的是
A. B.
C. D.

2. 下列各数中，能使不等式 x−3>0 成立的是
A. −3B. 5C. 3D. 2

3. 下列多项式中，不能运用公式进行分解因式的是
A. a2+b2B. x2−9C. m2−n2D. x2+2xy+y2

4. 下列分式中，是最简分式的是
A. 4xyx2B. 42x−6C. 3x+3D. x−yx2−y2

5. 已知一个多边形的内角和是 540∘，则这个多边形是
A. 四边形B. 五边形C. 六边形D. 七边形

6. 已知 aA. a+2b2D. −2a>−2b

7. 下列命题是真命题的是
A. 平行四边形对角线相等
B. 直角三角形两锐角互补
C. 不等式 −2x−1<0 的解是 x<−12
D. 多边形的外角和为 360∘

8. 化简 x2−y2x2+xy 的结果为
A. −yxB. −yC. x+yxD. x−yx

9. 如图，将 △ABC 绕点 A 逆时针旋转 110∘，得到 △ADE，若点 D 落在线段 BC 的延长线上，则 ∠B 大小为
A. 30∘B. 35∘C. 40∘D. 45∘

10. 如图在直角 △ABC 中，∠BAC=90∘，AB=8，AC=6，DE 是 AB 边的垂直平分线，垂足为 D，交边 BC 于点 E，连接 AE，则 △ACE 的周长为
A. 16B. 15C. 14D. 13

二、填空题（共6小题；共30分）
11. 分解因式：1−x2= ．

12. 在平行四边形 ABCD 中，∠A+∠C=200∘，则 ∠A= ．

13. 若 ab=−2，a+b=1，则代数式 a2b+ab2 的值等于 ．

14. 等边三角形中，两条中线所夹的锐角的度数为 ．

15. 对分式 12x，14y，18xy2 进行通分时，最简公分母是 ．

16. 如图，平行四边形 ABCD 的面积为 32，对角线 BD 绕着它的中点 O 按顺时针方向旋转一定角度后，其所在直线分别交 BC，AD 于点 E，F，若 AF=3DF，则图中阴影部分的面积等于 ．

三、解答题（共9小题；共117分）
17. 分解因式：3a2b−12ab+12b．

18. 解不等式组 x−3x−2≤4, ⋯⋯①2x−13>x−56. ⋯⋯②

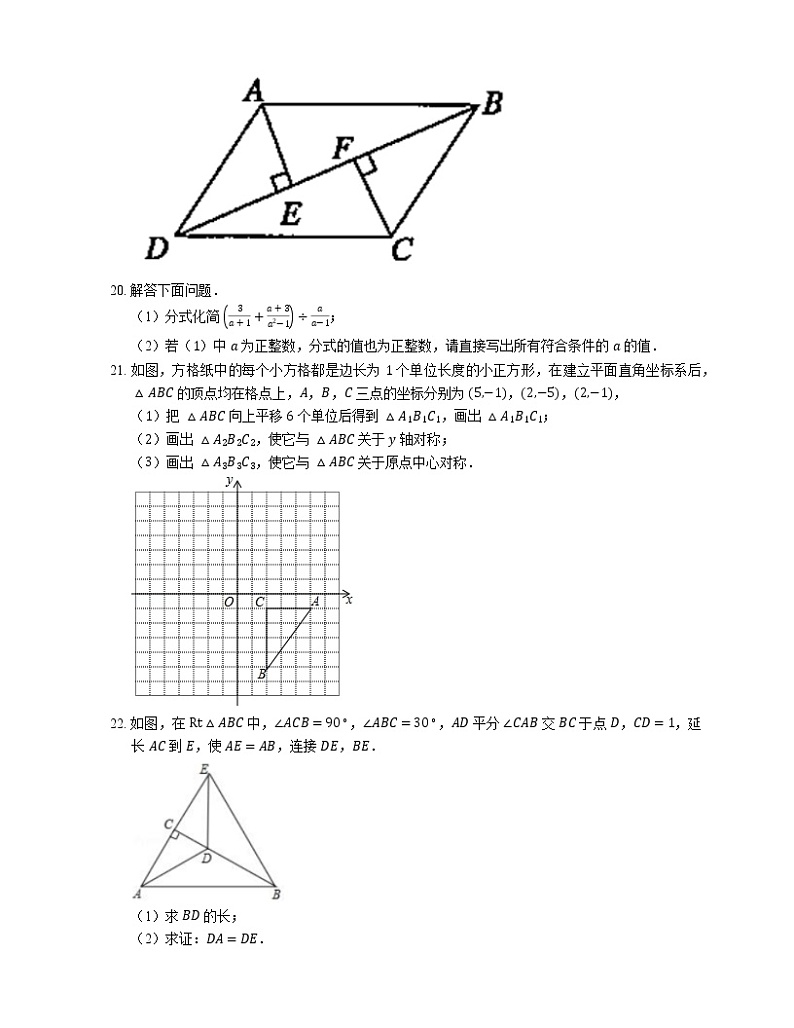
19. 已知（如图），在四边形 ABCD 中，AB=CD，过 A 作 AE⊥BD 交 BD 于点 E，过 C 作 CF⊥BD 交 BD 于 F，且 AE=CF．求证：四边形 ABCD 是平行四边形．

20. 解答下面问题．
（1）分式化简 3a+1+a+3a2−1÷aa−1；
（2）若（1）中 a 为正整数，分式的值也为正整数，请直接写出所有符合条件的 a 的值．

21. 如图，方格纸中的每个小方格都是边长为 1 个单位长度的小正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上，A，B，C 三点的坐标分别为 5,−1，2,−5，2,−1，
（1）把 △ABC 向上平移 6 个单位后得到 △A1B1C1，画出 △A1B1C1；
（2）画出 △A2B2C2，使它与 △ABC 关于 y 轴对称；
（3）画出 △A3B3C3，使它与 △ABC 关于原点中心对称．

22. 如图，在 Rt△ABC 中，∠ACB=90∘，∠ABC=30∘，AD 平分 ∠CAB 交 BC 于点 D，CD=1，延长 AC 到 E，使 AE=AB，连接 DE，BE．
（1）求 BD 的长；
（2）求证：DA=DE．

23. 根据《佛山-环西拓规划方案》，三水区域内改造提升的道路约 37 公里，届时，沿线将串联起狮山、乐平、三水新城、水都基地、白坭等城镇节点，在这项工程中，有一段 4000 米的路段由甲、乙两个工程队负责完成．已知甲工程队每天完成的工作量是乙工程队每天完成的工作量的 2 倍，且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用 20 天．求甲、乙两个工程队平均每天各完成多少米?

24. 如图，在 △ABC 中，AB=AC，点 D，E 分别是边 AB，AC 的中点，连接 DE，BE，点 F，G，H 分别为 BE，DE，BC 的中点．
（1）求证：FG=FH；
（2）若 ∠A=90∘，求证：FG⊥FH；
（3）若 ∠A=80∘，求 ∠GFH 的度数．

25. 如图所示，在平行四边形 ABCD 中，AD∥BC，过 B 作 BE⊥AD 交 AD 于点 E，AB=13 cm，BC=21 cm，AE=5 cm．动点 P 从点 C 出发，在线段 CB 上以每秒 1 cm 的速度向点 B 运动，动点 Q 同时从点 A 出发，在线段 AD 上以每秒 2 cm 的速度向点 D 运动，当其中一个动点到达端点时另一个动点也随之停止运动，设运动的时间为 t（秒）．
（1）当 t 为何值时，四边形 PCDQ 是平行四边形?
（2）当 t 为何值时，△QDP 的面积为 60 cm2?
（3）当 t 为何值时，PD=PQ?
答案
第一部分
1. C【解析】A、不是轴对称图形，也不是中心对称图形，故此选项错误；
B、不是轴对称图形，也不是中心对称图形，故此选项错误；
C、是轴对称图形，也是中心对称图形，故此选项正确；
D、不是轴对称图形，也不是中心对称图形，故此选项错误；
故选：C．
2. B【解析】不等式 x−3>0 的解集为：x>3．
3. A【解析】A、原式不能运用公式分解，错误；
B、 原式=x+3x−3；
C、 原式=m+nm−n；
D、 原式=x+y2，
故选：A．
4. C【解析】A、 4xyx2=4yx，不是最简分式；
B、 42x−6=2x−3，不是最简分式；
C、 3x+3，是最简分式；
D、 x−yx2−y2=x−yx+yx−y=1x+y，不是最简分式；
故选：C．
5. B
【解析】根据多边形的内角和可得：n−2180∘=540∘，
解得：n=5，则这个多边形是五边形．
6. C【解析】A、将 aB、将 aC、将 aD、将 a−2b，此不等式成立；
故选：C．
7. D【解析】平行四边形对角线不一定相等，A是假命题；
直角三角形两锐角互余，B是假命题；
不等式 −2x−1<0 的解是 x>−12，C是假命题；
多边形的外角和为 360∘，D是真命题．
8. D【解析】x2−y2x2+xy=x+yx−yxx+y=x−yx．
9. B【解析】∵△ABC 绕点 A 逆时针旋转 110∘，得到 △ADE，
∴AB=AD，∠BAD=110∘，
由三角形内角和 ∠B=180∘−∠BAD2=180∘−110∘2=35∘．
故选：B．
10. A
【解析】连接 AE．
∵ 在 Rt△ABC 中，∠BAC=90∘，AB=8，AC=6，
∴BC=AB2+AC2=10，
∵DE 是 AB 边的垂直平分线，
∴AE=BE，
∴△ACE 的周长为：AE+EC+AC=BE+CE+AC=BC+AC=10+6=16．
第二部分
11. 1+x1−x
【解析】1−x2=1+x1−x．
12. 100∘
【解析】因为四边形 ABCD 是平行四边形，
所以 ∠A=∠C，AB∥CD，
所以 ∠A+∠D=180∘，
又因为 ∠A+∠C=200∘，
所以 ∠A=100∘．
13. −2
【解析】∵ab=−2，a+b=1，
∴a2b+ab2=aba+b=−2×1=−2.
14. 60∘
【解析】如图．
∵ 等边三角形 ABC，AD，BE 分别是中线，
∴AD，BE 分别是角平分线，
∴∠1=∠2=12∠ABC=30∘，
∴∠3=∠1+∠2=60∘．
15. 8xy2
【解析】最简公分母是 8xy2．
16. 4
【解析】设 DF=a，则 AF=3a，AD=4a．
设 BC 和 AD 之间的距离为 h，
∵ 四边形 BACD 是平行四边形，
∴AD∥BE，AD=BC=4a，BO=OD，
∵BE∥AD，
∴△BEO∽△DFO，
∴BEDF=BODO=11，
∴BE=DF=a，
∵ 平行四边形 ABCD 的面积为 32，
∴4a×h=32，
∴ah=8，
∴ 阴影部分的面积
S=S△BEO+S△DFO=12×BE+DF12h=12×a+a×12h=12ah=4.
第三部分
17. 原式=3ba2−4a+4=3ba−22.
18. 解不等式 ①，得：
x≥1.
解不等式 ②，得：
x<32.
所以不等式组的解集为
1≤x<32.
19. ∵AE⊥BD，CF⊥BD，
∴∠AEB=∠CFD=90∘，
在 Rt△ABE 和 Rt△CDF 中，AB=CD,AE=CF,
∴Rt△ABE≌Rt△CDFHL，
∴∠ABE=∠CDF，
∴AB∥CD，
∵AB=CD，
∴ 四边形 ABCD 是平行四边形．
20. （1） 原式=4aa2−1⋅a−1a=4a+1.
（2） 由题意可知：a+1=1或2或4，
且 a+1≠0，a2−1≠0，a≠0，
所以 a=3．
21. （1）如图所示：△A1B1C1，即为所求；
（2）如图所示：△A2B2C2，即为所求；
（3）如图所示：△A3B3C3，即为所求．
22. （1） ∵ 在 Rt△ABC 中，∠ACB=90∘，∠ABC=30∘，AD 平分 ∠CAB，
∴∠CAB=60∘=2×∠CAD，
∴∠CAD=∠DAB=30∘，
∴∠DAB=∠DBA=30∘，
∴BD=DA=2CD=2．
（2） ∵AE=AB，在 Rt△ABC 中，∠ACB=90∘，∠B=30∘，
∴∠EAB=60∘，
∴△ABE 是等边三角形，
∵BC⊥AE，
∴AC=CE，
∵∠ACD=∠DCE=90∘，CD=CD，
∴Rt△DCA≌Rt△DCESAS，
∴DA=DE．
23. 设乙工程队平均每天完成 x 米，则甲工程队平均每天完成 2x 米，
根据题意得：
4000x−40002x=20.
解得：
x=100.
经检验，x=100 是原分式方程的解，且符合题意，
∴2x=200．
答：甲工程队平均每天完成 200 米，乙工程队平均每天完成 100 米．
24. （1） ∵AB=AC，点 D，E 分别是边 AB，AC 的中点，
∴BD=EC．
∵ 点 F，G，H 分别为 BE，DE，BC 的中点，
∴FG∥BD，GF=12BD；FH∥EC，FH=12EC．
∴FG=FH．
（2） 由（1），FG∥BD，
又 ∵∠A=90∘，
∴FG⊥AC．
∵FH∥EC，
∴FG⊥FH．
（3） 延长 FG 交 AC 于点 K．
∵FG∥BD，∠A=80∘，
∴∠FKC=∠A=80∘．
∵FH∥EC，
∴∠GFH=180∘−∠FKC=100∘．
25. （1） 由题意得，CP=t，AQ=2t，
所以 QD=21−2t，
因为 AD∥BC，
所以当 DQ=PC 时，四边形 PCDQ 是平行四边形，
则 21−2t=t，
解得，t=7，
所以当 t=7 时，四边形 PCDQ 是平行四边形．
（2） 在 Rt△ABE 中，BE=AB2−AE2=12，
由题意得，12×21−2t×12=60，
解得，t=112，
所以当 t=112 时，△QDP 的面积为 60 cm2．
（3） 作 PH⊥DQ 于 H，DG⊥BC 于 G，
则四边形 HPGD 为矩形，
所以 PG=HD，
由题意得，CG=AE=5，
所以 PG=t−5，
当 PD=PQ，PH⊥DQ 时，DH=12DQ，即 t−5=1221−2t，
解得，t=314，
则当 t=314 时，PD=PQ．