2018_2019学年天津市南开区七下期末数学试卷

这是一份2018_2019学年天津市南开区七下期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列调查中，适合采用全面调查（普查）方式的是
A. 了解天津市中小学学生课外阅读情况
B. 了解天津市空气质量情况
C. 了解天津市居民的环保意识情况
D. 了解七年级一班同学的视力情况

2. 916 的平方根是 ±34，用式子表示正确的是
A. ±916=34B. ±916=±34C. 916=34D. 916=±34

3. 已知 aA. a+m>b+mB. a−m>b−mC. −2a>−2bD. a2>b2

4. 关于“10”，下列说法不正确的是
A. 它是数轴上唯一一个距离原点 10 个单位长度的点表示的数
B. 它是一个无理数
C. 若 a<10D. 它可以表示面积为 10 的正方形的边长

5. 不等式组 4x+3>1,2x−8≤16−4x 的最小整数解是
A. 0B. −1C. 1D. 2

6. 在 △ABC 中，∠C=30∘，∠A 与 ∠B 的度数比是 1:2，则 ∠B 的度数
A. 30∘B. 50∘C. 100∘D. 120∘

7. 若点 Pa,b 在第四象限，则点 P 到 x 轴的距离是
A. aB. −aC. bD. −b

8. 如图，AB∥CD∥EF，则下列各式中正确的是
A. ∠1=180∘−∠3B. ∠1=∠3−∠2
C. ∠2+∠3=180∘−∠1D. ∠2+∠3=180∘+∠1

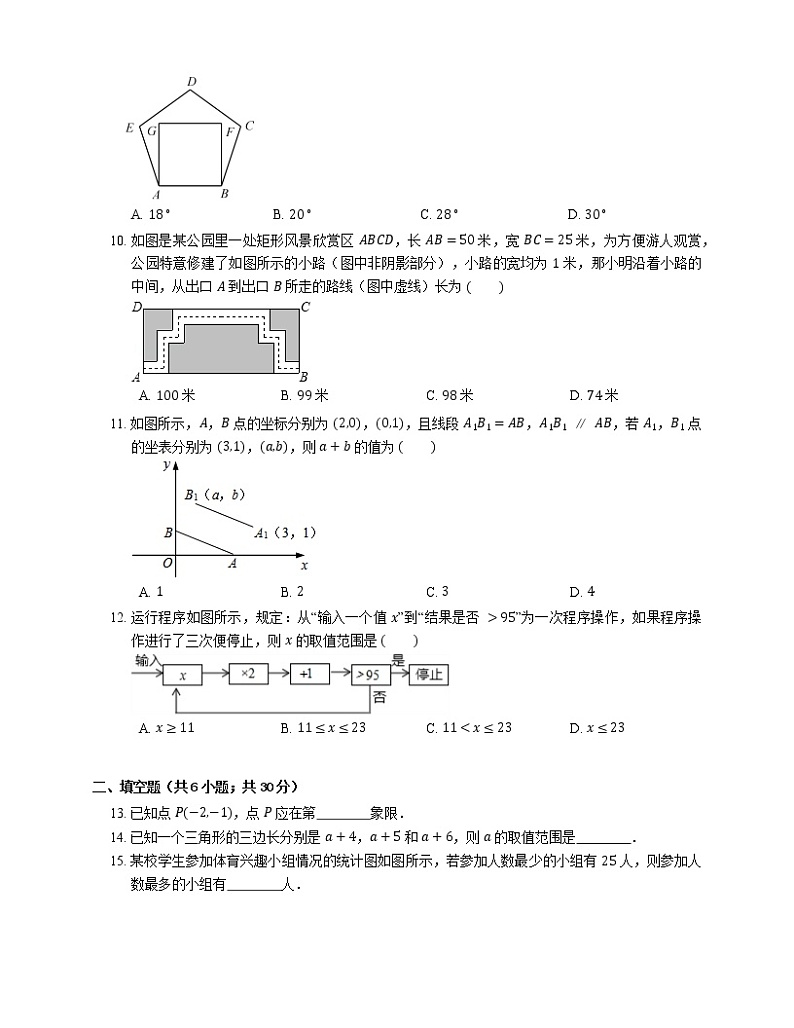
9. 把边长相等的正五边形 ABCDE 和正方形 ABFG 按照如图所示的方式叠合在一起，则 ∠EAG 的度数是
A. 18∘B. 20∘C. 28∘D. 30∘

10. 如图是某公园里一处矩形风景欣赏区 ABCD，长 AB=50 米，宽 BC=25 米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为 1 米，那小明沿着小路的中间，从出口 A 到出口 B 所走的路线（图中虚线）长为
A. 100 米B. 99 米C. 98 米D. 74 米

11. 如图所示，A，B 点的坐标分别为 2,0，0,1，且线段 A1B1=AB，A1B1∥AB，若 A1，B1 点的坐表分别为 3,1，a,b，则 a+b 的值为
A. 1B. 2C. 3D. 4

12. 运行程序如图所示，规定：从“输入一个值 x”到“结果是否 >95”为一次程序操作，如果程序操作进行了三次便停止，则 x 的取值范围是
A. x≥11B. 11≤x≤23C. 11
二、填空题（共6小题；共30分）
13. 已知点 P−2,−1，点 P 应在第 象限．

14. 已知一个三角形的三边长分别是 a+4，a+5 和 a+6，则 a 的取值范围是 ．

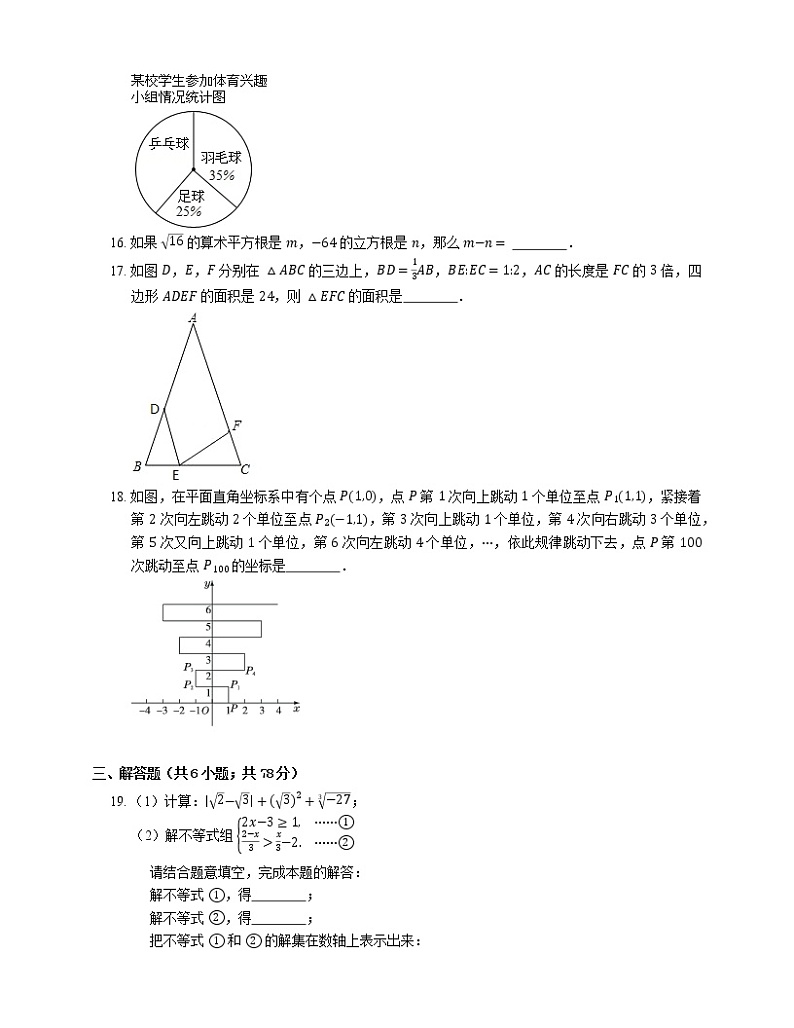
15. 某校学生参加体育兴趣小组情况的统计图如图所示，若参加人数最少的小组有 25 人，则参加人数最多的小组有 人．

16. 如果 16 的算术平方根是 m，−64 的立方根是 n，那么 m−n= ．

17. 如图 D，E，F 分别在 △ABC 的三边上，BD=13AB，BE:EC=1:2，AC 的长度是 FC 的 3 倍，四边形 ADEF 的面积是 24，则 △EFC 的面积是 ．

18. 如图，在平面直角坐标系中有个点 P1,0，点 P 第 1 次向上跳动 1 个单位至点 P11,1，紧接着第 2 次向左跳动 2 个单位至点 P2−1,1，第 3 次向上跳动 1 个单位，第 4 次向右跳动 3 个单位，第 5 次又向上跳动 1 个单位，第 6 次向左跳动 4 个单位，⋯，依此规律跳动下去，点 P 第 100 次跳动至点 P100 的坐标是 ．

三、解答题（共6小题；共78分）
19. （1）计算：2−3+32+3−27；
（2）解不等式组 2x−3≥1,⋯⋯①2−x3>x3−2.⋯⋯②
请结合题意填空，完成本题的解答：
解不等式 ①，得 ；
解不等式 ②，得 ；
把不等式 ① 和 ② 的解集在数轴上表示出来：
∴ 原不等式组的解集为 ．

20. 某校 1200 名学生参加了一场“安全知识”问答竞赛活动，为了解笔试情况，随机抽查了部分学生的得分情况，整理并制作了如图所示的图表（部分未完成），请根据图表提供的信息，解答下列问题：
分数段频数频率60≤x<70300.170≤x<8090n80≤x<90m0.490≤x<100600.2
（1）本次调查的样本容量为 ．
（2）在表中，m= ，n= ．
（3）补全频数分布直方图；
（4）如果比赛成绩 80 分以上（含 80 分）为优秀，本次竞赛中笔试成绩为优秀的大约有多少名学生?

21. 已知：如图，B，C，E 三点在同一直线上，A，F，E 三点在同一直线上，∠1=∠2=∠E，∠3=∠4．求证：AB∥CD．

22. （1）如图①，△ABC 是锐角三角形，高 BD，CE 相交于点 H，求出 ∠BHC 与 ∠A 的数量关系；
（2）如图②，△ABC 是钝角三角形，∠A>90∘，高 BD，CE 所在的直线相交于点 H，把图②补充完整，并说明 ∠BHC 与 ∠A 的数量关系与（1）中的结论是否一致．

23. 某学校为了庆祝校园艺术节，准备购买一批盆花布置校园．已知 1 盆A种花和 2 盆B种花一共需 13 元，2 盆A种花和 1 盆B种花一共需 11 元．
（1）求 1 盆A种花和 1 盒B种花的售价各是多少元?
（2）学校准备购进这两种盆花共 100 盆，并且A种盆花的数量不超过B种盆花数量的 2 倍，请求出A种盆花的数量最多是多少?

24. 如图，在长方形 OABC 中，O 为平面直角坐标系的原点，点 A 的坐标为 a,0，点 C 的坐标为 0,b，且 a，b 满足 a−4+∣b−6∣=0，点 B 在第一象限内，点 P 从原点出发，以每秒 2 个单位长度的速度沿着 O−C−B−A−O 的线路移动．
（1）点 B 的坐标为 ；当点 P 移动 3.5 秒时，点 P 的坐标为 ．
（2）在移动过程中，当点 P 到 x 轴的距离为 4 个单位长度时，求点 P 移动的时间．
答案
第一部分
1. D【解析】A．了解天津市中小学学生课外阅读情况适合抽样调查；
B．了解天津市空气质量情况适合抽样调查；
C．了解天津市居民的环保意识情况适合抽样调查；
D．了解七年级一班同学的视力情况适合普查．
2. B【解析】916 的平方根是 ±34，用式子表示正确的是 ±916=±34．
3. C【解析】A. a+mB. a−mC. −2a>−2b，正确；
D. a24. A【解析】A. ±10 它是数轴上离原点 10 个单位长度的点表示的数，题干的说法错误，符合题意；
B. 10 是一个无理数，题干的说法正确，不符合题意；
C.因为 3<10<3+1，a<10D. 10 表示面积为 10 的正方形的边长，题干的说法正确，不符合题意．
5. A
【解析】不等式组整理得：x>12,x≤4,
解得：−12则不等式组的最小整数解是 0．
6. C【解析】∵∠A 与 ∠B 的度数比是 1:2，
∴ 可以假设 ∠A=x，∠B=2x，
由题意：3x+30=180，
∴x=50，
∴∠B=100∘．
7. D【解析】∵ 点 Pa,b 在第四象限，
∴b<0，
∴ 点 P 到 x 轴的距离是 ∣b∣=−b．
8. D【解析】由图形可知，∠2+∠3−∠1=180∘，
所以 ∠2+∠3=180∘+∠1．
9. A【解析】∠EAG=180∘−360∘÷5−90∘=18∘．
10. C
【解析】根据已知可以得出此图形可以分为横向与纵向分析，横向距离等于 AB，纵向距离等于 AD−1×2，
所以长 AB=50 米，宽 BC=25 米，路线为 50+25−1×2=98 米．
11. C【解析】∵ 点 A2,0 平移后的对应点 A1 的坐标为 3,1，
∴ 平移的方式为向右平移 1 个单位，向上平移 1 个单位，
则点 B0,1 平移后的对应点 B1 的坐标为 1,2，
即 a=1，b=2，
∴a+b=3．
12. C【解析】有题意得：
2x+1≤95, ⋯⋯①22x+1+1≤95, ⋯⋯②222x+1+1+1>95, ⋯⋯③
解不等式 ① 得
x≤47.
解不等式 ② 得
x≤23.
解不等式 ③ 得
x＞11.
所以，x 的取值范围是 11第二部分
13. 三
【解析】∵ 点 P−2,−1，
∴ 点 P 应在第三象限．
14. a>−3
【解析】∵ 三角形的三边长分别为 a+4，a+5 和 a+6，
∴a+5−a−415. 40
【解析】参加兴趣小组的总人数 25÷25%=100（人），
参加乒乓球小组的人数 100×1−25%−35%=40（人）．
16. 6
【解析】∵16=4，4 的算术平方根是 2，
∴m=2．
∵−64 的立方根是 −4，
∴n=−4．
∴m−n=2−−4=2+4=6．
17. 8
【解析】连接 AE，
设 △BDE 的面积为 a，△EFC 的面积为 b，
BD=13AB，BE:EC=1:2，AC 的长度是 FC 的 3 倍，
∴△ADE 的面积为 2a，△AEF 的面积为 2b，
∵ 四边形 ADEF 的面积是 24，即 2a+2b=24，
∴△ABC 的面积为 a+b+24，BD=13AB，BE:EC=1:2，
∴BDAB=BEBC=13，
∵∠B=∠B，△BDE∽△BAC，S△BDES△BAC=132，
即 9a=a+b+24，
∴2a+2b=24,9a=a+b+24,
解得：a=4，b=8，
∴△EFC 的面积是 8．
18. 26,50
【解析】由图可知：以奇数开头的相邻两个坐标的纵坐标是相同的，所以第 100 次跳动后，纵坐标为 100÷2=50．
其中 4 的倍数的跳动得到的点都在 y 轴的右侧，那么第 100 次跳动得到的点也在 y 轴右侧．
P1 横坐标为 1，P4 横坐标为 2，P8 横坐标为 3，依此类推可得到：Pn 的横坐标为 n÷4+1（n 是 4 的倍数）．
故点 P100 的横坐标为 100÷4+1=26，纵坐标为 100÷2=50．
故点 P 第 100 次跳动至点 P100 的坐标是 26,50．
第三部分
19. （1） 原式=3−2+3+−3=3−2+3−3=3−2.
（2） x≥2；x<4；；2≤x<4
20. （1） 300
【解析】本次调查的样本容量为 30÷0.1=300．
（2） 120；0.3
【解析】m=300×0.4=120，n=90÷300=0.3．
（3） 补全直方图如图：
（4） 本次竞赛中笔试成绩为优秀的学生大约有 1200×0.4+0.2=720 人．
21. ∵∠2=∠E，
∴AD∥BC（内错角相等，两直线平行），
∴∠3=∠DAC（两直线平行，内错角相等），
∵∠3=∠4，
∴∠4=∠DAC，
∵∠1=∠2，
∴∠1+∠CAF=∠2+∠CAF，即 ∠BAF=∠DAC，
∴∠4=∠BAC，
∴AB∥CD（同位角相等，两直线平行）．
22. （1） 结论：∠BHC+∠A=180∘．
理由：∵ 高 BD，CE 相交于点 H，
∴∠AEH=∠ADH=90∘，
在四边形 AEHD 中，
∵∠AEH+∠ADH+∠A+∠EHD=360∘，
∴∠EHD+∠A=180∘，
∵∠BHC=∠EHD，
∴∠BHC+∠A=180∘．
（2） 图形如图 2 所示，结论不变，∠BHC+∠BAC=180∘．
理由：在四边形 ADHE 中，
∵∠AEH+∠ADH+∠DAE+∠EHD=360∘，
∴∠EHD+∠DAE=180∘，
∵∠BAC=∠DAE，
∴∠BHC+∠BAC=180∘．
23. （1） 1 盆A种花的售价为 x 元，1 盆B种花的售价是 y 元，
根据题意可得：
x+2y=13,2x+y=11,
解得：
x=3,y=5.
答：1 盆A种花的售价为 3 元，1 盆B种花的售价是 5 元．
（2） 设购进A种花 m 盆，
依据题意可得：
m≤2100−m,
解得：
m≤6623,
而 m 为正整数，
所以 m最多=66，
答：A种盆花最多购进 66 盆．
24. （1） 4,6；1,6
【解析】a，b 满足 a−4+∣b−6∣=0，
∴a−4=0，b−6=0，
解得 a=4，b=6，
∴ 点 B 的坐标是 4,6，
∵ 点 P 从原点出发，以每秒 2 个单位长度的速度沿着 O−C−B−A−O 的线路移动，
∴2×3.5=7，
∵OA=4，OC=6，
∴ 当点 P 移动 4 秒时，在线段 CB 上，离点 C 的距离是：7−6=1，
即当点 P 移动 4 秒时，此时点 P 在线段 CB 上，离点 C 的距离是 2 个单位长度，点 P 的坐标是 1,6．
（2） 由题意可得，在移动过程中，当点 P 到 x 轴的距离为 4 个单位长度时，存在两种情况，
第一种情况，当点 P 在 OC 上时，
点 P 移动的时间是：4÷2=2 秒，
第二种情况，当点 P 在 BA 上时，
点 P 移动的时间是：6+4+2÷2=6 秒，
故在移动过程中，当点 P 到 x 轴的距离为 4 个单位长度时，点 P 移动的时间是 2 秒或 6 秒．