初中数学鲁教版 (五四制)七年级上册5 一次函数的应用课文配套ppt课件

这是一份初中数学鲁教版 (五四制)七年级上册5 一次函数的应用课文配套ppt课件，共48页。PPT课件主要包含了旧知回顾，实际应用，课堂小结，深入探究，随堂练习，干旱造成的灾情，想一想，天后水库将干涸，110升，应用与延伸1等内容，欢迎下载使用。

1.由一次函数的图象可确定k和b的符号；2.由一次函数的图象可估计函数的变化趋势；3.可直接观察出：x与y的对应值；4.由一次函数的图象与y轴的交点的坐标可确定b值，从而由待定系数法确定一次函数的图象的解析式。
一次函数图象可获得哪些信息？
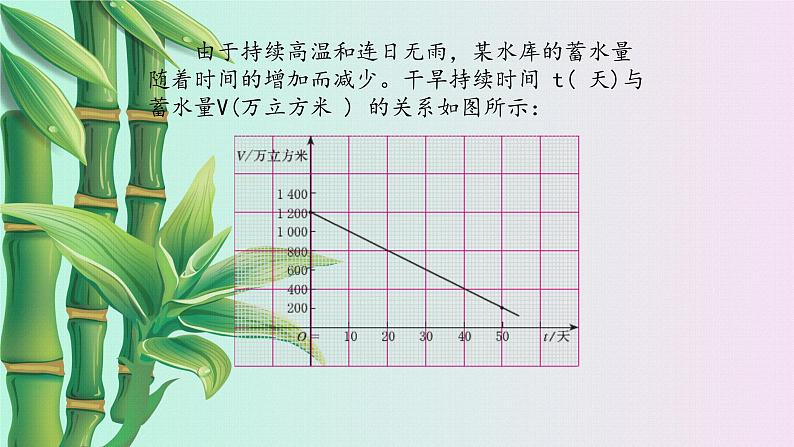
由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少。干旱持续时间 t( 天)与蓄水量V(万立方米 ) 的关系如图所示：
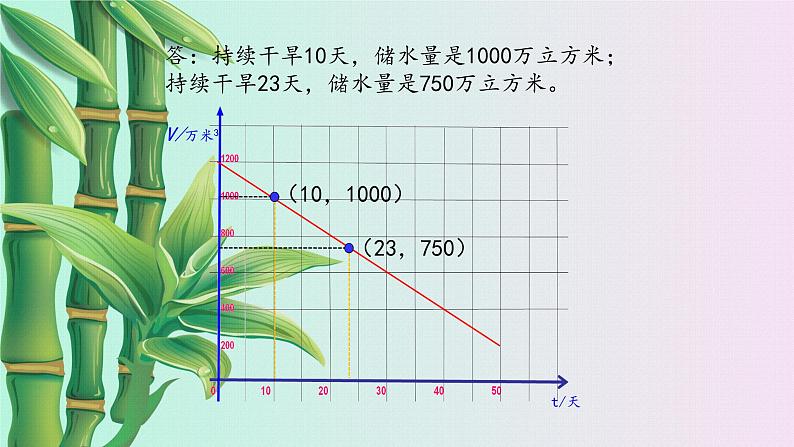
(2)干旱持续10天，蓄水量为多少？连续干旱23天呢？
分析：干旱10天求蓄水量就是已知自变量t=10求对应的因变量的值——数
体现在图象上就是找一个点，使点的横坐标是10，对应在图象上找到此点纵坐标的值（10，V）——形
(1)水库干旱前的蓄水量是多少？
分析：即t=0时的蓄水量，也就是1200万立方米。
答：持续干旱10天，储水量是1000万立方米；持续干旱23天，储水量是750万立方米。
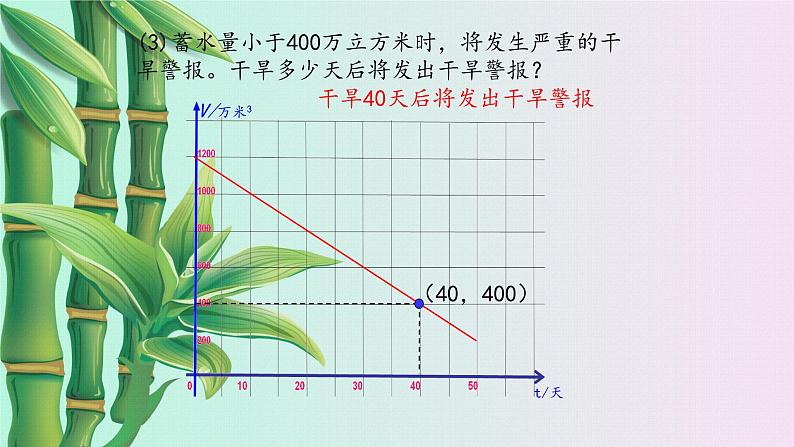
(3)蓄水量小于400万立方米时，将发生严重的干旱警报。干旱多少天后将发出干旱警报？
干旱40天后将发出干旱警报
(4)按照这个规律，预计干旱持续多少天水库将干涸？
合作探究：还能用其它方法解答本题吗？
（1）设v=kt+1200
（2）将t=10，V=1000代入V=kt+1200中求得 k=-20 V=-20t+1200
（3）再代入各组t或 V的值，得出对应的V与t的值
例1 某种摩托车的油箱加满油后，油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示：
(1)油箱最多可储油多少升？(2)一箱汽油可供摩托车行驶多少千米？ (3)摩托车每行驶100千米消耗多少升汽油？ (4)油箱中的剩余油量小于1升时将自动报警。行驶多少千米后，摩托车将自动报警？
(2)当y=0时，x=500，因此一箱汽油可供摩托车行驶500千米。
(3)x从100增加到200时，y从8减少到6，减少了2，因此摩托车每行驶100千米消耗2升汽油。
(4)当y=1时，x=450，因此行驶了450千米后，摩托车将自动报警。
总结：如何解答实际情景函数图象的信息？
1.理解横纵坐标分别表示的的实际意义
3.利用数形结合的思想： 将数转化为形 由形定数
2.分析已知（看已知的是自变量还是因变量），通过做x轴或y轴的垂线，在图象上找到对应的点，由点的横坐标或者纵坐标的值读出要求的值
上题中摩托车行至加油站加完油后，摩托车油箱的剩余油量y（升）和摩托车行驶路程x（千米）之间的关系变为图1：
试问：⑴加油站在多少千米处？加油多少升？
图1为加油后的图象
理由：由图象上观察的：400千米处设加油站，到700米处油用完，说明所加油最多可供行驶300千米。
（2）若乙地与加油站之间还有250千米，要到达乙地所加的油是否够用？
若加油之后变为图2呢的情况？观察图象变化，你看出了些什么？设想一下此时又发生了什么情况？
一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系？
1.从“数”的方面看，当一次函数y=0.5x+1的因变量的值为0时，相应的自变量的值即为方程0.5x+1=0的解。
2.从“形”的方面看，函数y=0.5x+1与x轴交点的横坐标，即为方程0.5x+1=0的解。
通过这节课的学习，你有什么收获？
1.通过一次函数的图象获取相关的信息；
3.初步体会方程与函数的关系，增强识图能力，应用能力。
2.①数形结合，函数与方程的思想 ②利用函数图象解决简单的实际问题
习题6.7 1，3
例1.如图，l1反映了某公司产品的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：
（1）当销售量为2吨时，销售收入＝　　　　元，　　 销售成本＝　　　　元；
⑵当销售量为6吨时，销售收入＝　　　　元， 销售成本＝　　　　元；
⑶当销售量为　　时，销售收入等于销售成本；
（4）当销售量　　　　时，该公司赢利　　 当销售量　　　　时，该公司亏损；
（5）l1对应的函数表达式是　　　　　　　　，　　 l2对应的函数表达式是　　　　　　　　。
y=500x+2000
例2.我边防局接到情报，近海处有一可疑船只A正向公海方向行驶。边防局迅速派出快艇B追赶（如下图）
下图中l1 ，l2分别表示两船相对于海岸的距离s（海里）与追赶时间t（分）之间的关系。
根据图象回答下列问题：
（1）哪条线表示B到海岸的距离与追赶时间之间的关系？
解：观察图象，得当t＝0时，B距海岸0海里，即S＝0，故l1表示B到海岸的距离与追赶时间之间的关系；
（2）A，B哪个速度快？
从0增加到10时，l2的纵坐标增加了2，而l1的纵坐标增加了5，即10分内，A行驶了2海里，B行驶了5海里，所以B的速度快。
（3）15 min内B能否追上A？
　　　　　可以看出，当t＝15时，l1上对应点在l2上对应点的下方，
这表明，15 min时B尚未追上A。
　　如图l1，l2相交于点P。
（4）如果一直追下去，那么B能否追上A？
因此，如果一直追下去，那么B一定能追上A。
（5）当A逃到离海岸12海里的公海时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？
从图中可以看出，l1与l2交点P的纵坐标小于12 ，
这说明在A逃入公海前，我边防快艇B能够追上A。
从图中可以看出，l1与l2交点P的纵坐标小于12，这说明在A逃入公海前，我边防快艇B能够追上A。
想一想你能用其他方法解决上述问题吗？
观察甲、乙两图，解答下列问题1.填空：两图中的 (____)图比较符合传统寓言故事《龟兔赛跑》中所描述的情节。
4.请你根据另一幅图表，充分发挥你的想象，自编一则新的“龟兔赛跑”的寓言故事，要求如下：（1）用简洁明快的语言概括大意，不能超过200字；（2）图表中能确定的数值，在故事叙述中不得少于3个，且要分别涉及时间、路和速度这三个量。
5.如图，lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系。（1）B出发时与A相距多少千米？（2）走了一段路后，自行车发生故障，进行修理，所用的时间是多少小时？（3）B出发后经过多少小时与A相遇？
（4）若B的自行车不发生故障，保持出发时的速度前进，那么经过多少时间与A相遇？相遇点离B的出发点多远？你能用哪些方法解决这个问题？在图中表示出这个相遇点C。
6.甲、乙两班参加植树活动，乙班先植树30棵，然后甲班才开始与乙班一起植树。设甲班植树的总量为y甲（棵），乙班植树的总量为y乙（棵），两班一起植树所用的时间（从甲班开始植树时计时）为x（时）， y甲、 y乙与 x之间的部分函数图象如图所示。
（1）当0≤x≤6时，分别求y甲、 y乙与x之间的函数关系式。（2）如果甲、乙两班均保持前6个小时的工作效率，通过计算说明，当x=8时，甲、乙两班植树的总量之和能否超过260棵。
（3）如果6个小时后，甲班保持前6个小时的工作效率，乙班通过增加人数，提高了工作效率，这样继续植树2小时，活动结束。当x=8时，两班之间植树的总量相差20棵，求乙班增加人数后平均每小时植树多少棵。
在运用一次函数解决实际问题时，首先判断问题中的两个变量之间是不是一次函数关系，当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果。
谈本节课你有什么收获？