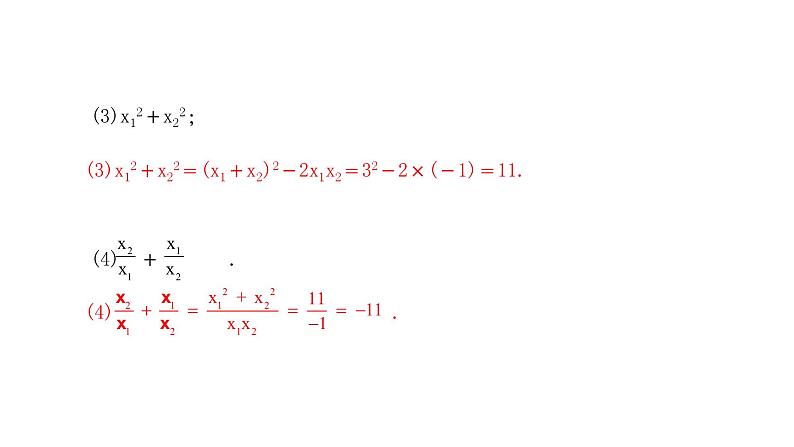
数学21.2.4 一元二次方程的根与系数的关系教学ppt课件

这是一份数学21.2.4 一元二次方程的根与系数的关系教学ppt课件，共17页。

知识点一　利用根与系数的关系求含方程两根的代数式的值
1.一元二次方程x2－2x＝0的两根分别为x1，x2，则x1x2的值为(　　)A.－2 B.1 C.2 D.02.方程2x2＋6x－1＝0的两根为x1，x2，则x1＋x2等于(　　)A.－6 B.6 C.－3 D.33.方程4x2＝5x－1的两根为x1，x2，则x1x2－x1－x2的值是(　　)A.1 B.－1 C. D.－
4.(课本P16练习改编)已知x1，x2是一元二次方程x2－3x－1＝0的两根，不解方程求下列各式的值：
(1) ＋ ； (2)(x1－1)(x2－1)；
(2)(x1－1)(x2－1)＝x1x2－(x1＋x2)＋1＝－1－3＋1＝－3.
(3)x12＋x22； (4) ＋ .
(3)x12＋x22＝(x1＋x2)2－2x1x2＝32－2×(－1)＝11.
知识点二　利用根与系数的关系求方程的根或字母的值
5.若关于x的方程2x2－ax＋2b＝0的两根和为4，积为－3，则a，b分别为(　)A.a＝－8，b＝－6 B.a＝4，b＝－3 C.a＝3，b＝8 D.a＝8，b＝－36.若关于x的一元二次方程x2－2x＋m＝0有一个根为x＝－1，则另外一个根为(　　)A.1 B.－3 C.3 D.4
8.已知x1，x2是关于x的方程x2＋bx－3＝0的两根，且满足x1＋x2－3x1x2＝5，那么b的值为(　　)
A.4 B.－4 C.3 D.－3
7.如果1是方程2x2＋bx－4＝0的一个根，那么方程的另一个根是(　　)A.－2 B.2 C.－1 D.1
9.已知关于x的方程x2－2x＋m＝0有两个不相等的实数根x1，x2.
(1)求实数m的取值范围；(2)若x1－x2＝2，求实数m的值.
解：(1)由题意，得Δ＝(－2)2－4×1×m＝4－4m＞0，解得m＜1.
易错点　利用根与系数的关系时，忽视前提条件Δ≥0
10.若关于x的方程x2＋(a－1)x＋a2＝0的两根互为倒数，则a的值为(　　)A.1或－1 B.1C.－1 D.011.关于x的一元二次方程x2＋2mx＋m2＋m＝0的两个实数根的平方和为12，则m的值为(　　)A.m＝－2 B.m＝3 C.m＝3或m＝－2 D.m＝－3或m＝2
12.已知x1，x2是关于x的方程x2－ax－2＝0的两根，下列结论一定正确的是 (　　)
A.x1＋x2＞0 B.x1x2＞0C.x1＜0，x2＜0 D.x1－x2≠013.甲、乙两同学解方程x2＋px＋q＝0，甲看错了一次项，得根2和7，乙看错了常数项，得根1和－10，则原方程为(　　)A.x2－9x＋14＝0 B.x2＋9x－14＝0C.x2－9x＋10＝0 D.x2＋9x＋14＝014.设a，b是方程x2＋2x－20＝0的两个实数根，则a2＋3a＋b的值为________.
考查角度一　根与系数的关系与根的判别式、不等式结合
15.关于x的一元二次方程x2＋2x＋k＋1＝0的实数根是x1和x2.(1)求k的取值范围；(2)如果x1＋x2－x1x2<－1，且k为整数，求k的值.
解：(1)由题意，得Δ＝4－4(k＋1)≥0，解得k≤0.
(2)由根与系数的关系，得x1＋x2＝－2，x1x2＝k＋1，∴－2－(k＋1)<－1，解得k>－2.又∵k≤0，且k为整数，∴k的值为－1或0.
考查角度二　代数式变形后利用根与系数的关系求值
16.已知关于x的一元二次方程x2＋(2m＋1)x＋m2－1＝0有两个不相等的实数根(1)求m的最小整数值；(2)若方程的两个实数根为x1，x2，且(x1－x2)2＋m2＝17，求m的值.
拔尖角度一　利用根与系数的关系构造方程
17.有些数学问题虽然表面与一元二次方程无关，但是我们能够通过构造一元二次方程，并利用一元二次方程的有关知识对其解决.下面介绍两种基本构造方法：方法1：利用根的定义构造.例如，若实数m，n满足m2－m－1＝0，n2－n－1＝0，且m≠n，则可将m，n看作是方程x2－x－1＝0的两个不相等的实数根.方法2：利用韦达定理逆向构造.例如，若实数a，b满足a＋b＝3，ab＝2，则可以将a，b看作是方程x2－3x＋2＝0的两个实数根.
根据上述材料解决下面问题：(1)已知实数m，n满足3m2－m－1＝0，3n2－n－1＝0，且m≠n，则m＋n＝__________，mn＝__________；(2)已知实数a，b，c满足a＋b＝c－5，ab＝ ，且c＜5，求c的最大值.