

2019年上海市徐汇区中考二模数学试卷(期中)
展开一、选择题(共6小题;共30分)
1. 在下列各式中,运算结果为 x2 的是
A. x4−x2B. x4⋅x−2C. x6÷x3D. x−12
2. 下列函数中,图象在第一象限满足 y 的值随 x 的值增大而减少的是
A. y=2xB. y=1xC. y=2x−3D. y=−x2
3. 关于 x 的方程 x2−mx−1=0 根的情况是
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 没有实数根D. 不能确定
4. 今年 3 月 12 日,学校开展植树活动,植树小组 16 名同学的树苗种植情况如表:
植树数棵35678人数25162
那么这 16 名同学植树棵树的众数和中位数分别是
A. 5 和 6B. 5 和 6.5C. 7 和 6D. 7 和 6.5
5. 下列说法,不正确的是
A. AB−AC=CB
B. 如果 ∣AB∣=∣CD∣,那么 AB=CD
C. a+b=b+a
D. 若非零向量 a=k⋅bk≠0,则 a∥b
6. 在四边形 ABCD 中,AB∥CD,AB=AD,添加下列条件不能推得四边形 ABCD 为菱形的是
A. AB=CDB. AD∥BCC. BC=CDD. AB=BC
二、填空题(共12小题;共60分)
7. 112 的倒数是 .
8. 2018 年 1 月,“墨子号”量子卫星实现了距离达 7600000 米的洲际量子密钥分发,数字 7600000 用科学记数法表示为 .
9. 在实数范围内分解因式 x3−4x 的结果为 .
10. 不等式组 x−2≥3,5−x>−2 的解集是 .
11. 方程 4−3x=x 的解是 .
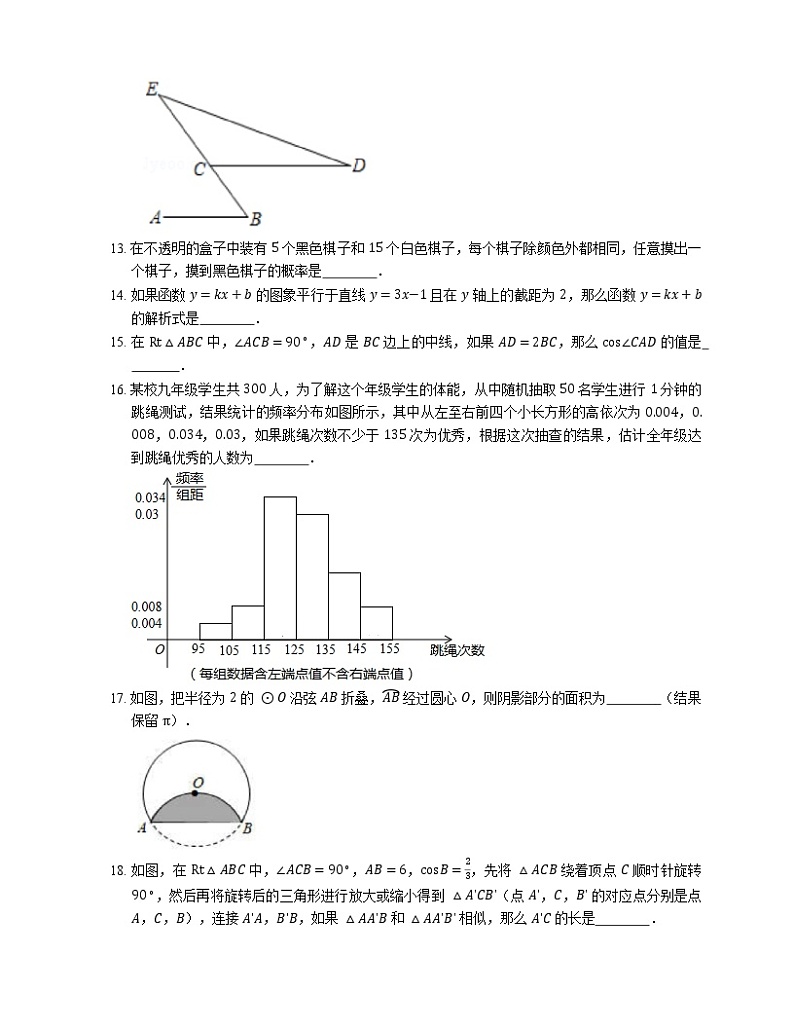
12. 如图,AB∥CD,若 ∠E=34∘,∠D=20∘,则 ∠B 的度数为 .
13. 在不透明的盒子中装有 5 个黑色棋子和 15 个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是 .
14. 如果函数 y=kx+b 的图象平行于直线 y=3x−1 且在 y 轴上的截距为 2,那么函数 y=kx+b 的解析式是 .
15. 在 Rt△ABC 中,∠ACB=90∘,AD 是 BC 边上的中线,如果 AD=2BC,那么 cs∠CAD 的值是 .
16. 某校九年级学生共 300 人,为了解这个年级学生的体能,从中随机抽取 50 名学生进行 1 分钟的跳绳测试,结果统计的频率分布如图所示,其中从左至右前四个小长方形的高依次为 0.004,0.008,0.034,0.03,如果跳绳次数不少于 135 次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为 .
17. 如图,把半径为 2 的 ⊙O 沿弦 AB 折叠,AB 经过圆心 O,则阴影部分的面积为 (结果保留 π).
18. 如图,在 Rt△ABC 中,∠ACB=90∘,AB=6,csB=23,先将 △ACB 绕着顶点 C 顺时针旋转 90∘,然后再将旋转后的三角形进行放大或缩小得到 △AʹCBʹ(点 Aʹ,C,Bʹ 的对应点分别是点 A,C,B),连接 AʹA,BʹB,如果 △AAʹB 和 △AAʹBʹ 相似,那么 AʹC 的长是 .
三、解答题(共7小题;共91分)
19. 计算:8+3−1−1+2−3−−32.
20. 解方程组:x2−xy−2y2=0,x2+2xy+y2=1.
21. 如图,已知 ⊙O 的弦 AB 长为 8,延长 AB 至 C,且 BC=12AB,tanC=12.求:
(1)⊙O 的半径;
(2)点 C 到直线 AO 的距离.
22. 某市植物园于 2019 年 3 月 −5 月举办花展,按照往年的规律推算,自 4 月下旬起游客量每天将增加 1000 人,游客量预计将在 5 月 1 日达到最高峰,并持续到 5 月 4 日,随后游客量每天有所减少,已知 4 月 24 日为第一天起,每天的游客量 y(人)与时间 x(天)的函数图象如图所示,结合图象提供的信息,解答下列问题:
(1)已知该植物园门票 15 元/张,若每位游客在园内每天平均消费 35 元,试求 5 月 1 日 −5 月 4 日,所有游客消费总额约为多少元?
(2)当 x≥11 时,求 y 关于 x 的函数解析式.
23. 如图,已知梯形 ABCD 中,AD∥BC,AB=AC,E 是边 BC 上的点,且 ∠AED=∠CAD,DE 交 AC 于点 F.
(1)求证:△ABE∽△DAF;
(2)当 AC⋅FC=AE⋅EC 时,求证:AD=BE.
24. 如图,在平面直角坐标系 xOy 中,抛物线 y=−14x2+bx+c 与直线 y=12x−3 分别交 x 轴、 y 轴上的 B,C 两点,设该抛物线与 x 轴的另一个交点为点 A,顶点为点 D,连接 CD 交 x 轴于点 E.
(1)求该抛物线的表达式及点 D 的坐标;
(2)求 ∠DCB 的正切值;
(3)如果点 F 在 y 轴上,且 ∠FBC=∠DBA+∠DCB,求点 F 的坐标.
25. 如图,△ABC 中,AC=BC=10,csC=35,点 P 是 AC 边上一动点(不与点 A,C 重合),以 PA 长为半径的 ⊙P 与边 AB 的另一个交点为 D,过点 D 作 DE⊥CB 于点 E.
(1)当 ⊙P 与边 BC 相切时,求 ⊙P 的半径.
(2)连接 BP 交 DE 于点 F,设 AP 的长为 x,PF 的长为 y,求 y 关于 x 的函数解析式,并直接写出 x 的取值范围.
(3)在(2)的条件下,当以 PE 长为直径的 ⊙Q 与 ⊙P 相交于 AC 边上的点 G 时,求相交所得的公共弦的长.
答案
第一部分
1. B【解析】x4 与 x2 不是同类项,不能合并,A选项错误;
x4⋅x−2=x2,B选项正确;
x6÷x3=x3,C选项错误;
x−12=x−2,D选项错误.
2. B【解析】A.y=2x 图象在第一象限满足 y 的值随 x 的值增大而增大,故此选项错误;
B.y=1x 图象在第一象限满足 y 的值随 x 的值增大而减小,故此选项正确;
C.y=2x−3 图象在第一象限满足 y 的值随 x 的值增大而增大,故此选项错误;
D.y=−x2 图象在第四象限满足 y 的值随 x 的值增大而减小,故此选项错误.
3. A【解析】Δ=−m2−4×1×−1=m2+4,
∵m2≥0,
∴m2+4>0,即 Δ>0,
∴ 方程有两个不相等的实数根.
4. D【解析】∵ 植树数为 3 的有 1 人,植树数为 5 的有 5 人,植树数为 6 的有 1 人,植树数为 7 的有 6 人,植树数为 8 的有 2 人,
∴ 出现次数最多的数据是 7,
∴ 众数为 7;
∵ 一共有 16 名同学,
∴ 因此其中位数应是第 8 和第 9 名数据的平均数,
∴ 中位数为 6+7÷2=6.5,故中位数为:6.5.
5. B
【解析】A、正确.∵AB=AC+CB,∴AB−AC=CB.不符合题意.
B、错误.模相等的向量不一定相等,符合题意.
C、正确.向量的解法返回加法交换律.不符合题意.
D、正确.根据平行向量的判定得出结论.不符合题意.
6. D【解析】A选项:若 AB=CD,
∵AB∥CD,
∴ 四边形 ABCD 是平行四边形,
当 AB=AD 可判定四边形 ABCD 是菱形;
B选项:当 AD∥BC 时,又 AB∥CD,
∴ 四边形 ABCD 是平行四边形,
当 AB=AD 可判定四边形 ABCD 是菱形;
C选项:当 BC=CD 时,△ABC≌△ACDSAS,
∴∠A=∠C.
∵AB∥CD,
∴∠C+∠ABC=180∘.
∴∠A+∠ABC=180∘.
∴AD∥BC.
又 AB∥CD,
∴ 四边形 ABCD 是平行四边形,
当 AB=AD 可判定四边形 ABCD 是菱形;
D选项只能说明四边形的三条边相等,所以不能判定是菱形.
第二部分
7. 23
【解析】112 的倒数是 1112=23.
8. 7.6×106
【解析】7600000=7.6×106.
9. xx+2x−2
【解析】x3−4x=xx2−4=xx+2x−2.
10. 5≤x<7
【解析】不等式组 x−2≥3, ⋯⋯①5−x>−2. ⋯⋯②
解 ① 式得 x≥5,
解 ② 式得 x<7.
故该不等式的解集为:5≤x<7.
11. x=1
【解析】原方程变形为 4−3x=x2,
整理得 x2+3x−4=0,
∴x+4x−1=0,
∴x+4=0 或 x−1=0,
∴x1=−4(舍去),x2=1.
12. 54∘
【解析】如图,
∵∠E=34∘,∠D=20∘,
∴∠BCD=∠D+∠E=20∘+34∘=54∘,
∵AB∥CD,
∴∠B=∠BCD=54∘.
13. 14
【解析】任意摸出一个棋子,摸到黑色棋子的概率 =55+15=14.
14. y=3x+2
【解析】∵ 函数 y=kx+b 的图象平行于直线 y=3x−1 且在 y 轴上的截距为 2,
∴k=3,b=2,
∴ 函数 y=kx+b 的解析式为 y=3x+2.
15. 154
【解析】设 CD=a,
∵AD 是 BC 边上的中线,
∴BC=2CD=2a,
∴AD=2BC=4a,
由勾股定理得,AC=AD2−CD2=15a,
∴cs∠CAD=ACAD=15a4a=154.
16. 72 人
【解析】∵ 从左至右前四个小长方形的高依次为 0.004,0.008,0.034,0.03,
∴ 从左至右前四个小组的频率为:0.04,0.08,0.34,0.3;
∴ 跳绳次数不少于 135 次的频率为 1−0.04−0.08−0.34−0.3=0.24,
∴ 全年级达到跳绳优秀的人数为 300×0.24=72 人.
17. 4π3−3
【解析】过 O 作 OD⊥AB 于 D,交劣弧 AB 于 E,如图:
∵ 把半径为 2 的 ⊙O 沿弦 AB 折叠,AB 经过圆心 O,
∴OD=DE=1,OA=2,
∵ 在 Rt△ODA 中,sinA=ODOA=12,
∴∠A=30∘,
∴∠AOE=60∘,
同理 ∠BOE=60∘,
∴∠AOB=60∘+60∘=120∘,
在 Rt△ODA 中,由勾股定理得:AD=OA2−OD2=22−12=3,
∵OD⊥AB,OD 过 O,
∴AB=2AD=23,
∴ 阴影部分的面积 S=S扇形AOB−S△AOB=120π×22360−12×23×1=4π3−3.
18. 35−5
【解析】由题意当点 Aʹ 在线段 BC 上且 AAʹ 平分 ∠BAC 时,△AAʹB 和 △AAʹBʹ 相似,作 AʹH⊥AB 于 H.
在 Rt△ABC 中,
∵csB=BCAB=23,AB=6,
∴BC=4,AC=62−42=25,
∵∠AʹAH=∠AʹAC,∠AHAʹ=∠ACAʹ=90∘,AAʹ=AAʹ,
∴△AAʹH≌△AAʹCAAS,
∴AʹC=AʹH,AC=AH=25,
设 AʹC=AʹH=x,
在 Rt△AʹBH 中,4−x2=x2+6−252,
∴x=35−5,
∴AʹC=35−5.
第三部分
19. 原式=22+13−1+3−2−3=22+3+12+3−2−3=323+2−52.
20.
x2−xy−2y2=0, ⋯⋯①x2+2xy+y2=1. ⋯⋯②
由 ① 得
x+yx−2y=0.
所以
x+y=0或x−2y=0.
由 ② 得
x+y2=1.
所以
x+y=1或x+y=−1.
所以原方程组化为 x+y=0,x+y=1 或 x+y=0,x+y=−1 或 x−2y=0,x+y=1 或 x−2y=0,x+y=−1,
所以原方程组的解为 x1=23,y1=13, x2=−23,y2=−13.
21. (1) 过 O 作 OD⊥AB 于 D,则 ∠ODC=90∘,
∵OD 过 O,
∴AD=BD,
∵AB=8,
∴AD=BD=4,
∵BC=12AB,
∴BC=4,
∴DC=4+4=8,
∵tanC=12=ODCD,
∴OD=4,
在 Rt△ODA 中,由勾股定理得:OA=OD2+AD2=42+42=42,
即 ⊙O 的半径是 42.
(2) 过 C 作 CE⊥AO 于 E,
则 S△AOC=12×AC×OD=12×AO×CE,
即 12×12×4=12×42×CE,
解得:CE=62,即点 C 到直线 AO 的距离是 62.
22. (1) 根据题意,得 5 月 1 日到 5 月 4 日每天的游客量均为:33000+7×1000=40000(人),
∴ 所有游客消费总额为:15+35×40000×4=8000000(元),
答:5 月 1 日到 5 月 4 日所有游客消费总额为 8000000 元.
(2) 设函数解析式为 y=kx+b,
把 11,40000 和 18,34400 都代入,得 40000=11x+b,34400=18x+b,
解得 k=−800,b=48800,
∴ 函数的解析式为:y=−800x+48800.
23. (1) ∵AD∥BC,
∴∠DAC=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAF=∠B,
∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠AED=∠CAD=∠ACB,
∴∠DEC=∠BAE,
∵AD∥BC,
∴∠DEC=∠ADF,
∴∠BAE=∠ADF,
∴△ABE∽△DAF.
(2) ∵AC⋅FC=AE⋅EC,AC=AB,
∴AB⋅FC=AE⋅EC,
∴ABEC=AEFC,
∵∠B=∠FCE,∠BAE=∠FEC,
∴△BAE∽△CEF,
∴ABEC=AEEF,
∴AEFC=AEEF,
∴FC=EF,
∴∠FEC=∠FCE,
∵∠FCE=∠B,
∴∠B=∠FEC,
∴AB∥DE,
∵AD∥BE,
∴ 四边形 ADEB 是平行四边形,
∴AD=BE.
24. (1) y=12x−3,令 y=0,则 x=6,令 x=0,则 y=−3,
则点 B,C 的坐标分别为 6,0,0,−3,则 c=−3,
将点 B 坐标代入抛物线 y=−14x2+bx−3 得:0=−14×36−6b−3,解得:b=2,
故抛物线的表达式为:y=−14x2+2x−3,令 y=0,则 x=6或−2,
即点 A2,0,则点 D4,1.
(2) 过点 E 作 EH⊥BC 交于点 H,
C,D 的坐标分别为:0,−3,4,1,
直线 CD 的表达式为:y=x−3,则点 E3,0,
tan∠OBC=OCOB=36=12,则 sin∠OBC=15,
则 EH=EB⋅sin∠OBC=35,
CE=32,则 CH=95,
则 tan∠DCB=EHCH=13.
(3) 点 A,B,C,D,E 的坐标分别为 2,0,6,0,0,−3,4,1,3,0,则 BC=35,
∵OE=OC,
∴∠AEC=45∘,tan∠DBE=16−4=12,
故:∠DBE=∠OBC,
则 ∠FBC=∠DBA+∠DCB=∠AEC=45∘,
①当点 F 在 y 轴负半轴时,过点 F 作 FG⊥BG 交 BC 的延长线与点 G,
则 ∠GFC=∠OBC=α,
设:GF=2m,则 CG=CGtanα=m,
∵∠CBF=45∘,
∴BG=GF,即:35+m=2m,解得:m=35,
CF=GF2+CG2=5m=15,
故点 F0,−18;
② 当点 F 在 y 轴正半轴时,同理可得:点 F0,2;
故:点 F 坐标为 0,2 或 0,−18.
25. (1) 设 ⊙P 与边 BC 相切的切点为 H,圆的半径为 R,连接 HP,
则 HP⊥BC,csC=35,则 sinC=45,
sinC=HPCP=R10−R=45,解得:R=409.
(2) 在 △ABC 中,AC=BC=10,csC=35,
设 AP=PD=x,∠A=∠ABC=β,
过点 B 作 BH⊥AC,
则 BH=ACsinC=8,
同理可得:CH=6,HA=4,AB=45,则:tan∠CAB=2,
BP=82+x−42=x2−8x+80,
DA=255x,则 BD=45−255x,
如图所示,PA=PD,
∴∠PAD=∠CAB=∠CBA=β,tanβ=2,
则 csβ=15,sinβ=25,
EB=BDcsβ=45−255x×15=4−25x,
∴PD∥BE,
∴EBPD=BFPF,即:4−25xx=x2−8x+80−yy,
整理得:y=5x3x+20x2−8x+800
∵ 点 Q 时弧 GD 的中点,
∴DG⊥EP,
∵AG 是圆 P 的直径,
∴∠GDA=90∘,
∴EP∥BD,
由(2)知,PD∥BC,
∴ 四边形 PDBE 为平行四边形,
∴DP=BE,即:x=4−25x,
解得:x=207,
GD=2GPsin∠GPE=2xsinβ=1657,
即:相交所得的公共弦的长为 1657.
2023年上海市徐汇区中考数学二模试卷(含解析): 这是一份2023年上海市徐汇区中考数学二模试卷(含解析),共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年上海市徐汇区中考数学二模试卷(含解析): 这是一份2022年上海市徐汇区中考数学二模试卷(含解析),共24页。试卷主要包含了14)0+13+2+−2.,【答案】B,【答案】C,【答案】,【答案】x=7,【答案】1,【答案】254等内容,欢迎下载使用。
2022年上海市徐汇区中考二模数学试卷: 这是一份2022年上海市徐汇区中考二模数学试卷,文件包含2022徐汇二模试题docx、答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。












