2020-2021年江苏省东台市八年级上学期数学第一次月考试卷 (1)

这是一份2020-2021年江苏省东台市八年级上学期数学第一次月考试卷 (1)，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
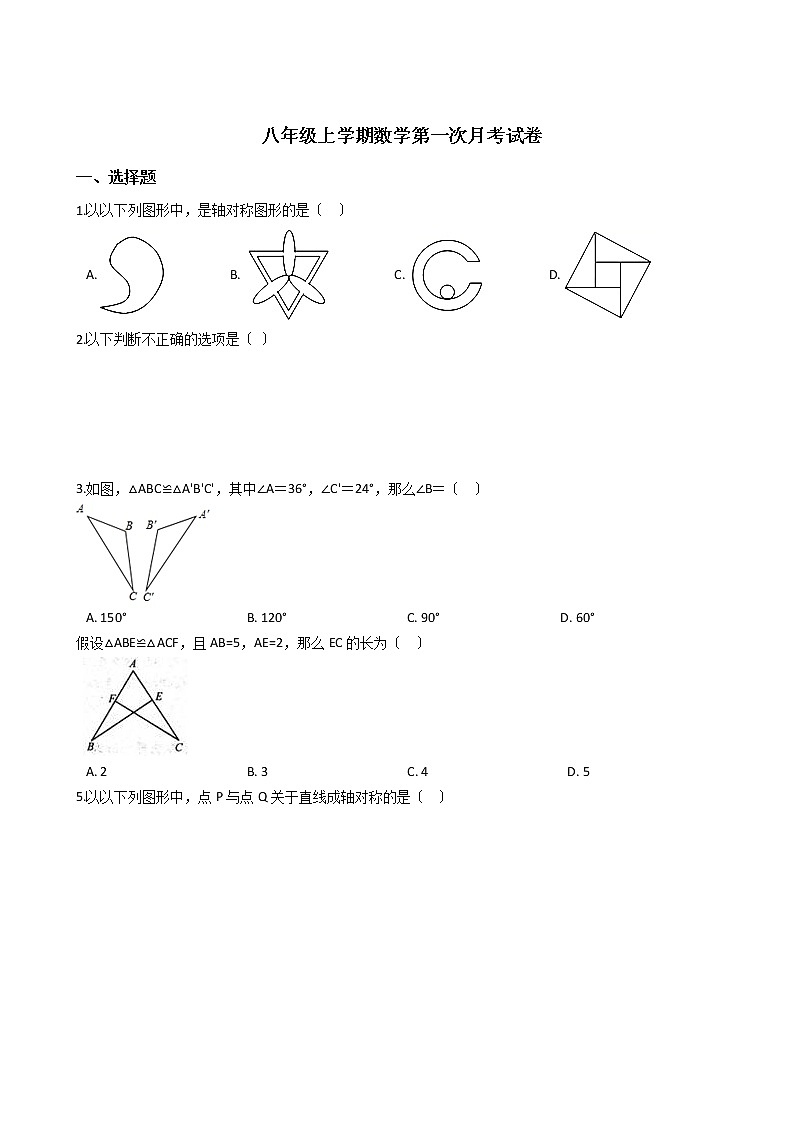
  八年级上学期数学第一次月考试卷一、选择题1.以以下列图形中，是轴对称图形的是〔   〕            A.                    B.                    C.                    D. 2.以下判断不正确的选项是〔 〕 


 3.如图，△ABC≌△A'B'C'，其中∠A＝36°，∠C'＝24°，那么∠B＝〔   〕  A. 150°                                     B. 120°                                     C. 90°                                     D. 60°假设△ABE≌△ACF，且AB=5，AE=2，那么EC的长为〔   〕   A. 2                                           B. 3                                           C. 4                                           D. 55.以以下列图形中，点P与点Q关于直线成轴对称的是〔   〕            A.                                       B. 
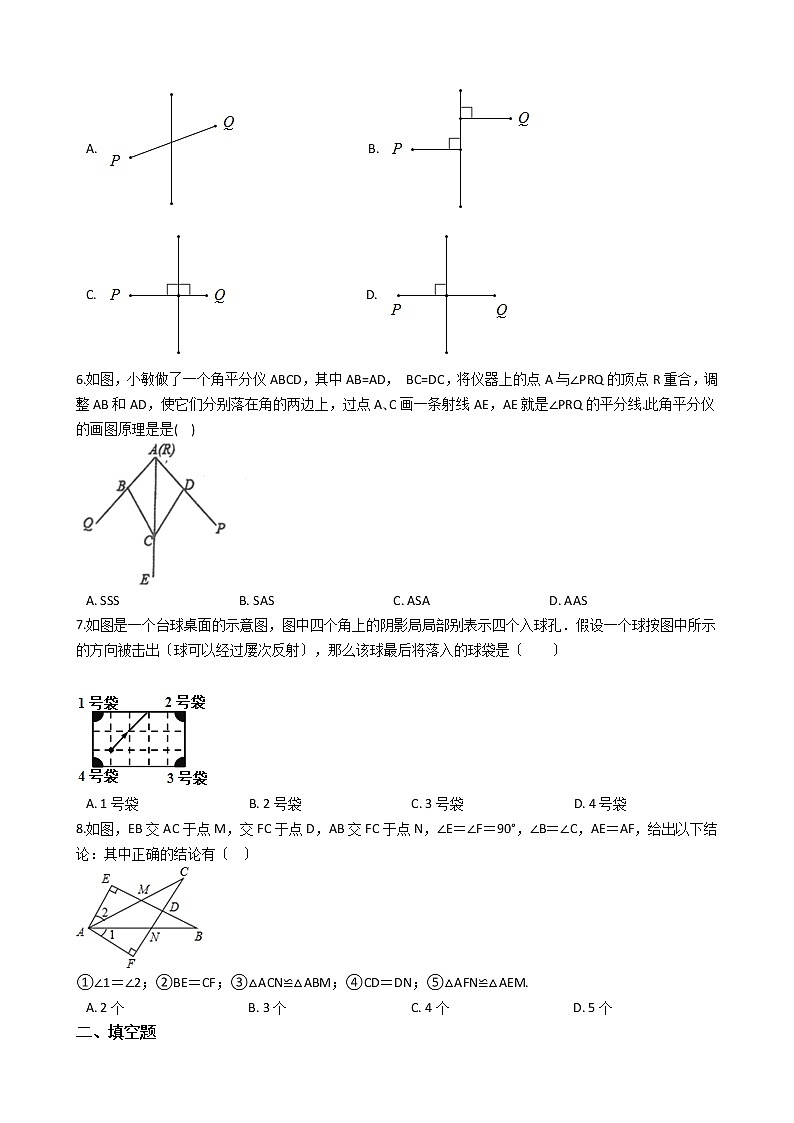
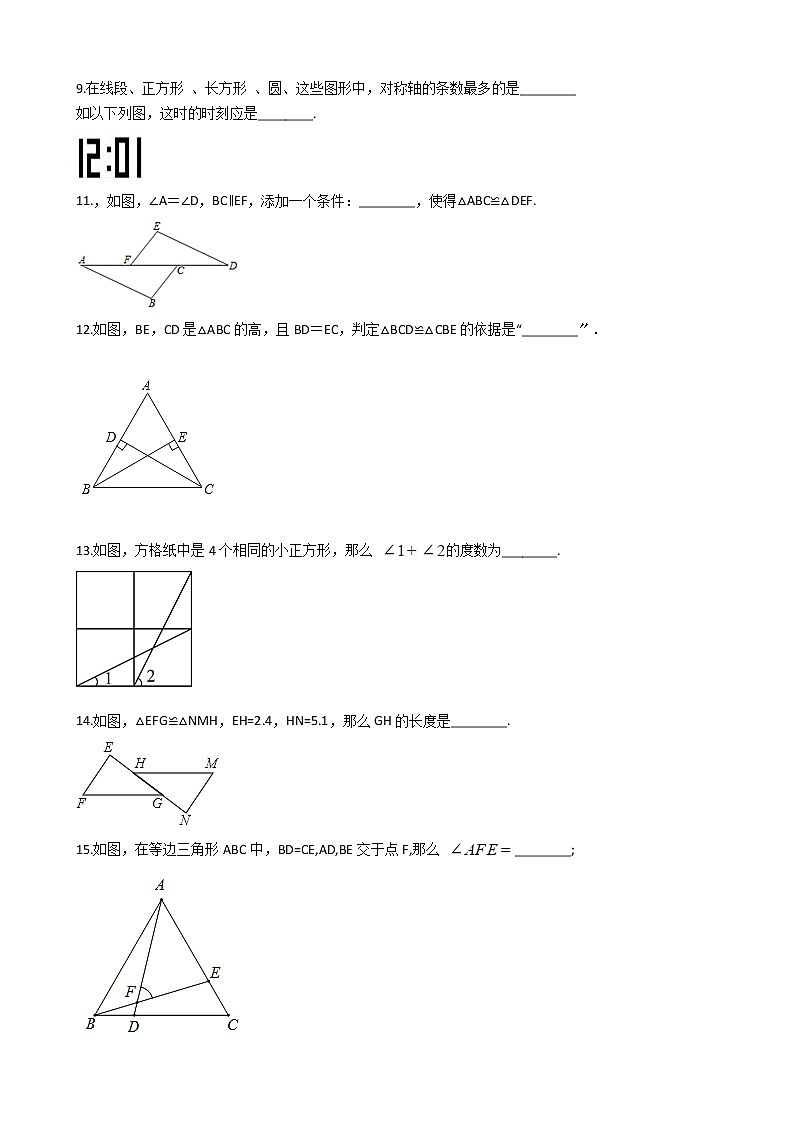
C.                                         D. 6.如图，小敏做了一个角平分仪ABCD，其中AB=AD， BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A､C画一条射线AE，AE就是∠PRQ的平分线.此角平分仪的画图原理是是(    )  A. SSS                                     B. SAS                                     C. ASA                                     D. AAS7.如图是一个台球桌面的示意图，图中四个角上的阴影局局部别表示四个入球孔．假设一个球按图中所示的方向被击出〔球可以经过屡次反射〕，那么该球最后将落入的球袋是〔　　〕 A. 1号袋                                  B. 2号袋                                  C. 3号袋                                  D. 4号袋8.如图，EB交AC于点M，交FC于点D，AB交FC于点N，∠E＝∠F＝90°，∠B＝∠C，AE＝AF，给出以下结论：其中正确的结论有〔   〕  ①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN；⑤△AFN≌△AEM.A. 2个                                       B. 3个                                       C. 4个                                       D. 5个二、填空题9.在线段、正方形 、长方形 、圆、这些图形中，对称轴的条数最多的是________    如以下列图，这时的时刻应是________.  11.，如图，∠A＝∠D，BC∥EF，添加一个条件：________，使得△ABC≌△DEF.  12.如图，BE，CD是△ABC的高，且BD＝EC，判定△BCD≌△CBE的依据是“________〞．  13.如图，方格纸中是4个相同的小正方形，那么 的度数为________.  14.如图，△EFG≌△NMH，EH=2.4，HN=5.1，那么GH的长度是________.  15.如图，在等边三角形ABC中，BD=CE,AD,BE交于点F,那么 ________;  16.如图，Rt△ABC中，∠ACB＝90°，∠A＝50°，将其折叠，使点A落在边CB上A′处，折痕为CD  ， 那么∠A′DB的度数为________．  17.如图，有一个直角三角形ABC，∠C＝90°，AC ，BC ，线段PQ AB，点Q在过点A且垂直于AC的射线AX上来回运动，点P从C点出发，沿射线CA以 的速度运动，问P点运动________  秒时 t ，才能使 ABC≌ QPA全等.  18.如图，在四边形ABCD中，给出了以下三个论断：①对角线AC平分∠BAD；②CD＝BC；③∠D＋∠B＝180°.在上述三个论断中，假设以其中两个论断作为条件，另外一个论断作为结论，那么可以得出________个正确的命题.  三、解答题19.如图，两个三角形成轴对称，画出对称轴.  20.直线MN和同侧两点AB，在MN上找一点P，使得PA+PB最小.   21.如图，AD∥BC，点E是CD 的中点，BE的延长线与AD的延长线交于点F.那么△BCE和△FDE全等吗?为什么?  22.如图，△ABF≌△CDE.  〔1〕假设∠B＝30°，∠DCF＝40°，求∠EFC的度数；    〔2〕假设BD=10，EF=2，求BF的长.    23.如图， ， ， .
 求证：〔1〕；    〔2〕.    24.如图，在 中，D是 的中点， ，垂足分别是 .  求证：AD平分 .25.如图四边形ABCD中，AB=AD=BC，点E在边BC上，∠EAD+∠BAC=90°，AE=5，AC=6，请求出△AED的面积. 
答案解析局部一、选择题1.【解析】【解答】解：A、不是轴对称图形，故本选项不符合题意； B、是轴对称图形，故本选项符合题意；C、不是轴对称图形，故本选项不符合题意；D、不是轴对称图形，故本选项不符合题意.故答案为：B. 【分析】在平面内，如果一个图形沿一条直线折叠，直线两旁的局部能够完全重合，那么这个图形叫做轴对称图形；根据定义并结合图形即可判断求解.2.【解析】【解答】A、两个形状相同的图形大小不一定相等，故本项错误；根据能够完全重合的两个图形叫做全等形，可得：B、能够完全重合的两个三角形全等正确，故本项错误；
C、全等图形的形状和大小都相同正确，故本项错误；
D、根据全等三角形的性质可得：全等三角形的对应角相等，故本选项正确；
应选：A．【分析】根据能够完全重合的两个图形叫做全等形，结合各项说法作出判断即可．此题考查了全等形的概念和三角形全等的性质：1、能够完全重合的两个图形叫做全等形，2、全等三角形的对应边相等；全等三角形的对应角相等；全等图形的形状和大小都相同，做题时要细心体会．3.【解析】【解答】解： △ABC≌△A'B'C' 又 故答案为：B.【分析】根据三角形全等，对应角相等，再通过三角形内角和定理，即可求出答案.4.【解析】【解答】解： ∵△ABE≌△ACF，
∴AC=AB=5，
∴EC=AC-AE=5-2=3.
故答案为：B. 【分析】根据全等三角形对应边相等得AC的长，结合AE=2，从而求出EC的长.5.【解析】【解答】解：点P和点Q关于直线成轴对称，那么直线和线段PQ的位置关系是：直线垂直平分PQ. 故答案为：D.【分析】点P与点Q关于直线成轴对称，根据轴对称的性质，有直线垂直平分PQ.6.【解析】【解答】在 和 ∴ 〔SSS〕∴ 故答案为：A.【分析】由用边边边可证△ABC≌△ADC，根据全等三角形的对应角相等可求解.7.【解析】【解答】如以下列图， 该球最后落入2号袋． 应选B．【分析】根据网格结构利用轴对称的性质作出球的运动路线，即可进行判断．8.【解析】【解答】∵∠E＝∠F＝90°，∠B＝∠C，AE＝AF， ∴△ABE≌△ACF〔AAS〕，∴BE＝CF，AF＝AE，故②正确，∠BAE＝∠CAF，∠BAE−∠BAC＝∠CAF−∠BAC，∴∠1＝∠2，故①正确，∵△ABE≌△ACF，∴AB＝AC，又∠BAC＝∠CAB，∠B＝∠C△ACN≌△ABM〔ASA〕，故③正确，CD＝DN不能证明成立，故④错误∵∠1＝∠2，∠F＝∠E，AF＝AE，∴△AFN≌△AEM〔ASA〕，故⑤正确，故答案为：C.【分析】①正确.可以证明△ABE≌△ACF可得结论.②正确，利用全等三角形的性质可得结论.③正确，根据ASA证明三角形全等即可.④错误，本结论无法证明.⑤正确.根据ASA证明三角形全等即可.二、填空题9.【解析】【解答】解：线段有1条对称轴； 正方形有4条对称轴；长方形有2条对称轴；圆有无数条对称轴；故答案为：圆. 【分析】如果沿某条直线对折，对折的两局部是完全重合的，那么就称这样的图形为轴对称图形，这条直线叫做这个图形的对称轴.根据定义结合图形特征即可求解.10.【解析】【解答】解：关于镜子的像，实际数字与原来的数字关于竖直的线对称，根据相应数字的对称性可得实际时间.∵是从镜子中看，∴对称轴为竖直方向的直线，∵2的对称数字是5，镜子中数字的顺序与实际数字顺序相反，∴这时的时刻应是10：51. 故答案为：10：51. 【分析】根据镜面对称的性质，镜中看到的数字是左右对调，而上下不对调即可直接得出答案。11.【解析】【解答】可添加BC=EF，理由： ∵BC∥EF，∴∠ACB=∠DFE，∵∠A=∠D，BC=EF，∴△ABC≌△DEF〔AAS〕，故答案为：BC=EF〔答案不唯一〕.【分析】由平行线的性质可证得∠ACB=∠DFE，由，要使△ABC≌△DEF，可添加AB=DE〔AAS〕或BC=EF〔AAS〕或AC=DF〔SAS〕等，答案不唯一.12.【解析】【解答】因为BE，CD是△ABC的高，所以∠CDB=∠BEC=90°, △CDB和△BEC是直角三角形；且BD＝EC，BC=CB所以△BCD≌△CBE； 【分析】首先根据三角形的高可得两个高所在的三角形是直角三角形，再根据由一组直角边和一组斜边相等，利用直角三角形的判断方法，可得两个直角三角形全等． 13.【解析】【解答】解：如图，根据方格纸的性质， 在△ABD和△CBE中，∴△ABD≌△CBE〔SAS〕，∴∠1=∠BAD，∵∠BAD+∠2=90°，∴ =90°.故答案为：90°.【分析】首先证明三角形全等，根据全等三角形的性质可得对应角相等，再由余角的定义和等量代换可得∠1与∠2的和为90°.14.【解析】【解答】解：∵△EFG≌△NMH， ∴EG=HN=5.1，∴GH=EG﹣EH=5.1﹣2.4=2.7.故答案为：2.7.【分析】根据全等三角形的性质求出EG，结合图形计算，得到答案.15.【解析】【解答】解：在等边△ABC中，AB=BC，∠ABC=∠C=60°， 在△ABD和△BCE中，∵ ，∴△ABD≌△BCE〔SAS〕，∴∠BAD=∠CBE，在△ABF中，∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=∠ABC=60°，即∠AFE=60°.故答案为：60°.【分析】根据等边三角形的性质可得AB=BC，∠ABC=∠C=60°，然后利用“边角边〞证明△ABD和△BCE全等，根据全等三角形对应角相等可得∠BAD=∠CBE，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFE=∠ABC，从而得解.16.【解析】【解答】解：∵∠ACB＝90°，∠A＝50°， ∴∠B＝90°﹣50°＝40°，∵折叠后点A落在边CB上A′处，∴∠CA′D＝∠A＝50°，由三角形的外角性质得，∠A′DB＝∠CA′D﹣∠B＝50°﹣40°＝10°．故答案为：10°．【分析】根据直角三角形两锐角互余求出∠B，根据翻折变换的性质可得∠CA′D=∠A，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．17.【解析】【解答】∵ ABC≌ QPA， ∴BC＝PA＝6，①当点P在线段CA上时，CP＝AC－AP＝10－6＝4，∴P点运动时间为： 〔秒〕，②当点P在线段CA的延长线上时，CP＝AC＋AP＝10＋6＝16，∴P点运动时间为： 〔秒〕，综上所述，P点运动时间为：2秒或8秒，故填：2或8.【分析】根据题意 ABC≌ QPA，可知对应边BC＝PA，再进行分析计算.18.【解析】【解答】〔1〕共有：①②作为条件，③作为结论， ①③作为条件，②作为结论，②③作为条件，①作为结论，3种情况，都是真命题，故可以写出3个正确的命题；故答案为3.【分析】过点C作CE⊥AB，CF⊥AD，垂足为E、F，①②作为条件，可以证明△CBE与△CDF全等，根据全等三角形对应角相等可得∠B=∠CDF，再根据平角定义得到∠B+∠D=180°，所以③作为结论是正确的命题；①③作为条件，与前一种情况的思路相反，可以根据条件证明△CBE与△CDF全等，再根据全等三角形对应边相等得到CD=BC，所以②作为结论是正确的命题；②③作为条件，先证明∠B=∠CDF，再根据“角角边〞证明△CBE与△CDF全等，根据全等三角形对应边相等可得CE=CF，再根据到角的两边距离相等的点在角的平分线上可得AC平分∠BAD，所以①作为结论是正确命题；三、解答题19.【解析】【分析】连接一对对应点AB，作AB的垂直平分线即可得出答案20.【解析】【分析】作点B关于直线MN的对称点B′，那么PB=P B′，根据 两点之间线段最短可得，当点A、P、B′共线时，PA+PB=PA+P B′最短，故连接AB′与MN的交点即为所求作的点P.21.【解析】【分析】根据AD∥BC，可得∠BCE=∠FDE,∠CBE=∠DFE，点E是CD的中点，可得CE=DE，即可判断△BCE和△FDE全等.22.【解析】【分析】〔1〕根据全等三角形的对应角相等得出 ∠B=∠D =30°，进而根据三角形外角定理，由 ∠EFC=∠D+∠DCF 就可算出答案；
〔2〕根据全等三角形对应边相等得出BF=DE ，根据等式的性质，由等量减去等量差相等得出 BE=DF ，然后根据 BE+DF=BD-EF 及 BF=BE+EF 就可算出答案.23.【解析】【分析】〔1〕先由平行线的性质得∠B=∠C，从而利用SAS判定△ABF≌△DCE；〔2〕根据全等三角形的性质得∠AFB=∠DEC，由等角的补角相等可得∠AFE=∠DEF，再由平行线的判定可得结论.24.【解析】【分析】首先证明 ，然后有 ，再根据角平分线性质定理的逆定理即可证明.25.【解析】【分析】作BF⊥AC于F，DG⊥AE于G，那么由等腰三角形的三线合一证得AF=CF=3，再证明△ADG≌△BAF，证得DG=AF=3，然后由三角形的面积公式即可得出结论.