2020-2021年江苏省兴化市九年级上学期数学12月月考试卷及答案

这是一份2020-2021年江苏省兴化市九年级上学期数学12月月考试卷及答案，共10页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

九年级上学期数学12月月考试卷
一、单项选择题
1.2x﹣5y＝0，那么x：y的值为〔   〕
A. 2：5                                    B. 5：2                                    C. 3：2                                    D. 2：3
2.相似三角形△ABC和△A′B′C′的面积比为1：4，那么它们的相似比为〔   〕
A. 1：4                                    B. 1：3                                    C. 1：2                                    D. 1：1
3.抛物线y＝x2+2x+3的顶点坐标是〔   〕
A. 〔﹣1，﹣2〕                      B. 〔﹣1，2〕                      C. 〔1，2〕                      D. 〔1，﹣2〕
2+2x﹣4＝0的一个根是1，那么k的值是〔   〕
A. ﹣1                                         B. ﹣2                                         C. 1                                         D. 2
5.抛物线 与x轴只有一个交点，那么m的值为〔       〕
A. － 6                                          B. 6                                          C. 3                                          D. 9
6.如图， A、B 两点的坐标分别为〔﹣2，0〕、〔0，1〕，⊙C 的圆心坐标为〔0，﹣1〕，半径为 1，E 是⊙C 上的一动点，那么△ABE 面积的最大值为〔   〕

A.                                B. 3+                                C. 3+                                D. 4+
二、填空题
7. 是一元二次方程，那么k=________.
8.假设⊙P的半径为5，圆心P的坐标为〔﹣3，4〕，那么平面直角坐标系的原点O与⊙P的位置关系是________．
9.如图，在圆内接四边形ABCD中，∠B＝100°，那么∠D的度数为________．

2－3x＋2＝0的两根为x1 ， x2 ， 那么x1＋x2＋x1x2的值为________．
11.某品牌运动服原来每件售价640元，经过两次降价，售价降为360元，两次降价的百分率相同，那么每次降价的百分率为________.
12.如图，在正六边形ABCDEF中，AC＝2 ，那么它的边长是________．

13.在半径为5cm的圆中，有一点P满足OP＝3cm，那么过点P的最短弦长为________cm．
14.在函数y＝x2+2x+2中，假设﹣5≤x≤5，那么函数y的最小值是________．
15.如图，抛物线y＝ax2+c与直线y＝mx+n交于A〔﹣1，p〕，B〔2，q〕两点，那么不等式ax2-mx+c＞n的解集是________．

16.关于x的函数y=〔m﹣1〕x2+2x+m图象与坐标轴只有2个交点，那么m=________.
三、解答题
以下方程：
〔1〕〔2x﹣1〕2＝4
〔2〕x2+3x﹣1＝0
以下条件的二次函数的解析式．
〔1〕图象经过点A〔1，0〕，B〔0，﹣3〕，对称轴是直线x＝2；
〔2〕图象顶点坐标是〔﹣2，3〕，且过点〔1，﹣3〕；
19.往水平放置的圆柱形油槽内装入一些油后，截面如以下列图．假设油面宽AB和油的最大深度都为80cm．

〔1〕求油槽的半径OA；
〔2〕从油槽中放出一局部油，当剩下的油面宽度为60cm时，求油面下降的高度．
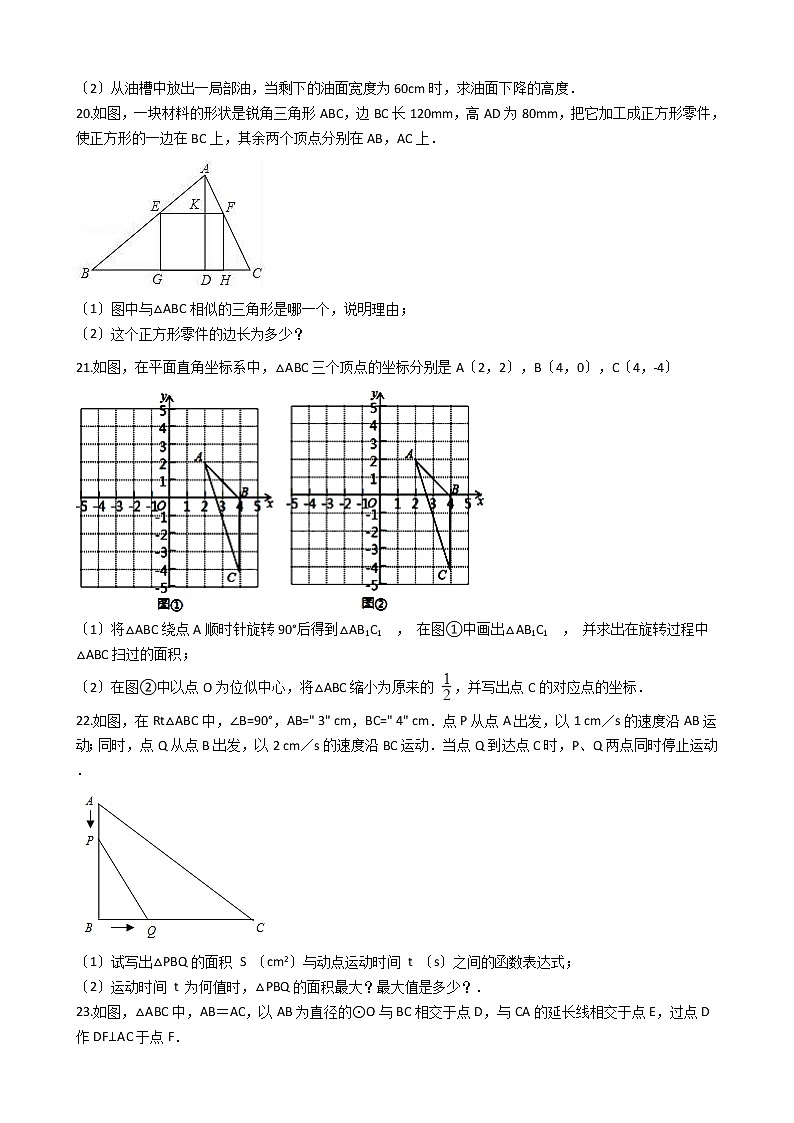
20.如图，一块材料的形状是锐角三角形ABC，边BC长120mm，高AD为80mm，把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．

〔1〕图中与△ABC相似的三角形是哪一个，说明理由；
〔2〕这个正方形零件的边长为多少？
21.如图，在平面直角坐标系中，△ABC三个顶点的坐标分别是A〔2，2〕，B〔4，0〕，C〔4，﹣4〕

〔1〕将△ABC绕点A顺时针旋转90°后得到△AB1C1 ， 在图①中画出△AB1C1 ， 并求出在旋转过程中△ABC扫过的面积；
〔2〕在图②中以点O为位似中心，将△ABC缩小为原来的 ，并写出点C的对应点的坐标．
22.如图，在Rt△ABC中，∠B=90°，AB=" 3" cm，BC=" 4" cm．点P从点A出发，以1 cm／s的速度沿AB运动；同时，点Q从点B出发，以2 cm／s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．

〔1〕试写出△PBQ的面积 S 〔cm2〕与动点运动时间 t 〔s〕之间的函数表达式；
〔2〕运动时间 t 为何值时，△PBQ的面积最大？最大值是多少？．
23.如图，△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．

〔1〕证明：DF是⊙O的切线；
〔2〕假设AC＝3AE，FC＝6，求AF的长．
24.某商店以每件60元的价格购进一批商品，现以单价80元销售，每月可售出300件．经市场调查发现：每件商品销售单价每上涨1元，该商品平均每月的销售量就减少10件，设每件商品销售单价上涨了x元．
〔1〕假设销售单价上涨了3元，那么该商品每月销售量为________件；
〔2〕当每件商品销售单价上涨多少元时，该商店每月的销售利润为6160元？
〔3〕写出月销售该商品的利润y〔元〕与每件商品销售单价上涨x〔元〕之间的函数关系式；当销售单价定为多少元时，每月销售该商品的利润最大？最大利润为多少？
25.对于二次函数y＝x2﹣4x+3和一次函数y＝﹣x+1，我们把y＝t〔x2﹣4x+3〕+〔1﹣t〕〔﹣x+1〕称为这两个函数的“再生二次函数〞，其中t是不为零的实数，其图象记作抛物线E．现有点A〔1，0〕和抛物线E上的点B〔2，n〕，请完成以下任务：
〔1〕【尝试】判断点A是否在抛物线E上；
〔2〕求n的值．
〔3〕【发现】通过〔1〕和〔2〕的演算可知，对于t取任何不为零的实数，抛物线E总过定点，请你求出定点的坐标．
〔4〕【应用】二次函数y＝﹣3x2+8x﹣5是二次函数y＝x2﹣4x+3和一次函数y＝﹣x+1的一个“再生二次函数〞吗？如果是，求出t的值；如果不是，说明理由．
26.在平面直角坐标系xOy中，抛物线y＝ax2﹣4ax+3a﹣2〔a≠0〕的对称轴与x轴交于点A，将点A向右平移3个单位长度，向上平移2个单位长度，得到点B．
〔1〕点A的坐标为________，点B的坐标为________；
〔2〕假设a＝﹣1，当m﹣1≤x≤m+1时，函数y＝ax2﹣4ax+3a﹣2的最大值为﹣10，求m的值；
〔3〕假设抛物线与线段AB有公共点，求a的取值范围．

答案解析局部
一、单项选择题
1.【解析】【解答】∵2x﹣5y＝0
∴2x=5y
∴x:y=5:2
故答案为：B.
【分析】移项后，利用比例的性质可得出结果.
2.【解析】【解答】解：∵相似三角形△ABC和△A′B′C′的面积比为1：4，
∴它们的相似比为1：2，
应选：C．
【分析】根据相似三角形面积的比等于相似比的平方解答即可．
3.【解析】【解答】解：∵y＝x2+2x+3=
∴顶点坐标为〔-1,2〕
故答案为：B.
【分析】将抛物线改写为顶点式，即可得出顶点坐标.
4.【解析】【解答】将1代入kx2+2x﹣4＝0得：k+2-4=0，
解得k=2，
故答案为：D.
【分析】将1代入方程，得到关于k的一元一次方程，即可求解.
5.【解析】【解答】∵二次函数y=x2﹣6x+m的图象与x轴只有一个公共点，∴y=0时，方程x2﹣6x+m=0有两个相等的实数根，∴△=62﹣4×1×m=0．
解得：m=9．
故答案为：D．
【分析】根据二次函数y=x2﹣6x+m的图象与x轴只有一个公共点，可知y=0时，方程x2﹣6x+m=0有两个相等的实数根，从而可以求得m的值．
6.【解析】【解答】如图，过点C作CD⊥AB，延长DC交⊙C于E，此时△ABE面积的最大值〔AB是定值，只要圆上一点E到直线AB的距离最大即可〕，

设直线AB的解析式为y＝kx+b〔k≠0〕，
∵A〔﹣2，0〕，B〔0，1〕，
∴ ，
解得 ，
∴直线AB的解析式为 y＝ x+1 ①，
∵CD⊥AB，C〔0，﹣1〕，
∴直线CD的解析式为y＝﹣2x﹣1 ②，
联立①②得，D〔﹣ ， 〕，
∴CD＝ ＝ ，
∵⊙C的半径为1，
∴DE＝CD+CE＝ +1，
∵A〔﹣2，0〕，B〔0，1〕，
∴AB＝ ，
∴S△ABE的最大值＝ AB•DE＝ 〔 +1〕× ＝2+ .
故答案为： A.
【分析】过点C作CD⊥AB，延长DC交⊙C于E，此时△ABE面积的最大值，点E在过点C垂直于AB的直线和圆C在点C下方的交点，然后求出直线AB解析式，进而得出CD解析式，即可得出点D坐标，再求出CD，进而得出DE，再用三角形的面积公式即可得出结论．
二、填空题
7.【解析】【解答】解：∵ 是一元二次方程，∴ ，解得： .
故答案为：4.
【分析】将一个方程化为一般形式后，如果只含有一个未知数，且未知数的最高次数是2，二次项的系数不为0的整式方程就是一元二次方程，根据定义即可求出k的值.
8.【解析】【解答】解：由勾股定理，得
OP＝ ＝5，
d＝r＝5，
故点O在⊙P上．
故答案为点O在⊙P上.
【分析】由勾股定理等性质算出点与圆心的距离d，那么d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
9.【解析】【解答】∵圆内接四边形ABCD中，∠B＝100°，
∴∠D=180°-100°=80°
故答案为：80°.

【分析】根据圆内接四边形的对角互补即可求出答案.
10.【解析】【解答】解：∵x1 ， x2是方程x2－3x＋2＝0的两根，
∴x1+ x2＝ ，x1x2＝ ，
∴x1＋x2＋x1x2＝3+2＝5.
故答案为：5.

【分析】根据根与系数的关系分别求出两根之和及两根之积，再整体代入即可求出答案.
11.【解析】【解答】设每次降价的百分率为x，根据题意列方程得，
640 =360，解得 〔舍去〕；
∴ ；
故答案为： .
【分析】设每次降价的百分率为x，根据降价后的价格=降价前的价格〔1-降价的百分率〕，那么第一次降价后的价格是640〔1-x〕，第二次后的价格是640 ，据此即可列方程求解．
12.【解析】【解答】如图，过B作BG⊥AC于点G，

正六边形每个内角为 ，
∴∠ABC=120°，∠BAC=∠BCA=30°，
∵在等腰△ABC中，BA=BC，BG⊥AC，
∴AG=GC= AC= ，
在Rt△ABG中，cos∠BAG=
∴
故答案为：2.
【分析】过B作BG⊥AC于点G，易求正六边形的内角度数为120°，所以∠BAG=30°，在Rt△ABG中，利用三角函数可求出AB.
13.【解析】【解答】如图，过点P最短弦为与直径垂直的弦AB，连接OA，

∵CD⊥AB于点P，
∴AB=2AP，∠APO=90°，
在Rt△AOP中，AP= =4cm，
∴AB=8cm.
∴过点P的最短弦为8cm.
故答案为：8.
【分析】首先根据题意作图，然后根据题意与图可知最短弦为与直径垂直的弦AB，由垂径定理即可求得AB=2AP，然后在Rt△AOP中，利用勾股定理即可求得AP的长，那么可求得答案．
14.【解析】【解答】 ，
，
，
∵ ，﹣5≤-1≤5，
∴当 时，函数有最小值
故答案为1．
【分析】把二次函数解析式整理成顶点式形式，然后根据抛物线开口向上，在对称轴处取得最小值即可得出答案．
15.【解析】【解答】∵不等式ax2-mx+c＞n可变形为ax2+c＞mx+n，
∴图像上抛物线在直线上方时对应x的范围即为不等式的解集，
观察函数图象可知：当﹣1＜x＜2时,抛物线y=ax2+c在直线y=mx+n的上方，
∴不等式ax2-mx+c>n的解集为﹣1＜x＜2.
故答案为：﹣1＜x＜2.
【分析】将不等式变形为ax2+c＞mx+n，观察图像即可得出结论.
16.【解析】【解答】解：〔1〕当m﹣1=0时，m=1，函数为一次函数，解析式为y=2x+1，与x轴交点坐标为〔﹣ ，0〕；与y轴交点坐标〔0，1〕.符合题意.〔2〕当m﹣1≠0时，m≠1，函数为二次函数，与坐标轴有两个交点，那么过原点，且与x轴有两个不同的交点，
于是△=4﹣4〔m﹣1〕m＞0，
解得，〔m﹣ 〕2＜ ，
解得m＜ 或m＞ .
将〔0，0〕代入解析式得，m=0，符合题意.〔3〕函数为二次函数时，还有一种情况是：与x轴只有一个交点，与Y轴交于交于另一点，
这时：△=4﹣4〔m﹣1〕m=0，
解得：m= .
故答案为：1或0或 .
【分析】分类讨论：〔1〕当m﹣1=0时，m=1，函数为一次函数，该函数与纵坐标只有两个交点；〔2〕当m﹣1≠0时，m≠1，函数为二次函数，与坐标轴有两个交点，那么过原点，且与x轴有两个不同的交点，此时根的判别式的值大于0，且m=0；〔3〕函数为二次函数时，还有一种情况是：与x轴只有一个交点，与Y轴交于交于另一点，此时根的判别式等于0，从而列出方程，求解即可，综上所述即可得出答案。
三、解答题
17.【解析】【分析】〔1〕采用直接开方法即可求解；〔2〕采用公式法解一元二次方程
18.【解析】【分析】〔1〕设顶点式 ，然后代入A、B坐标，求出a、k的值，即可得到解析式；〔2〕设顶点式 ，代入〔1，-3〕求出a的值，即可得到解析式.
19.【解析】【分析】〔1〕过O作OC⊥AB，延长CO与圆交于D，利用垂径定理得到AC的长度，设OA为xcm，然后在Rt△OAC中利用勾股定理建立方程求解；〔2〕当油面下降到EF位置时，作出图形，连接OF，设CD与EF交于点G，在Rt△OGF中，利用勾股定理求出OG，那么下降高度为OC+OG.
20.【解析】【分析】〔1〕根据矩形的对边平行得到BC∥EF，利用“平行于三角形的一边的直线截其他两边或其他两边的延长线，得到的三角形与原三角形相似〞判定即可．〔2〕设正方形零件的边长为x mm，那么KD=EF=x，AK=80-x，根据EF∥BC，得到△AEF∽△ABC，根据相似三角形的性质得到比例式，解方程即可得到结果．
21.【解析】【分析】〔1〕利用旋转的性质作图，根据扇形面积求法以及三角形面积求法得出面积；〔2〕根据位似图形的作法作图，再根据对应点的位置写出坐标．
22.【解析】【分析】〔1〕利用t表示出BP、BQ，利用三角形的面积计算方法列出关于t的函数关系式；〔2〕利用〔1〕中的函数探讨最大值问题即可．
23.【解析】【分析】〔1〕连接OD，根据等边对等角性质和平行线的判定和性质证得OD⊥DF，从而证得DF是⊙O的切线；〔2〕根据圆周角定理、勾股定理得出BE=2 AE，CE=4AE，然后根据勾股定理求得BE=2 AE，再根据相似三角形的判定与性质，即可得到答案．
24.【解析】【解答】〔1〕当单价上涨3元时，销量为300﹣10×3＝270，故答案为：270
【分析】〔1〕单价上涨x〔元〕，根据单价每上涨1元，该商品每月的销量就减少10件得到销售量为〔300-10x〕件，代入x=3求得结果即可；〔2〕根据题意列出一元二次方程求得答案即可；〔3〕把得到的函数关系式进行配方得到y=-10〔x-5〕2+6250，然后根据二次函数的最值问题易得到单价定为多少元时，每月销售该商品的利润最大．
25.【解析】【分析】〔1〕【尝试】将x=1代入y＝t〔x2﹣4x+3〕+〔1﹣t〕〔﹣x+1〕计算后进行判断；〔2〕将x=2代入 y＝t〔x2﹣4x+3〕+〔1﹣t〕〔﹣x+1〕即可求解；(3)【发现】将抛物线E的表达式进行因式分解后，通过观察式子特点，即可得出经过的定点；(4) 【应用】根据“再生二次函数〞的定义列出等式即可求解．
26.【解析】【解答】解：〔1〕抛物线的对称轴为直线x＝﹣ ＝2，
∴点A的坐标为〔2，0〕．
∵将点A向右平移3个单位长度，向上平移2个单位长度，得到点B，
∴点B的坐标为〔2+3，0+2〕，即〔5，2〕．
故答案为：〔2，0〕，〔5，2〕；
【分析】〔1〕利用对称轴公式可求出对称轴，即可得到A点坐标，然后利用点的平移得到B点坐标；〔2〕将a＝﹣1代入抛物线解析式，将解析式整理成为顶点式，找到对称轴，然后利用函数图象的增减性进行讨论即可得出答案；〔3〕分a＞0和a＜0两种情况考虑，画出抛物线与AB相交的图像，数形结合可得a的取值范围.