
2020-2021年浙江省宁波市九年级上学期数学12月月考试卷及答案
展开 九年级上学期数学12月月考试卷
一、选择题〔共12小题,4*12=48〕
1.假设3x=2y〔xy≠0〕,那么以下比例式成立的是〔 〕
A. B. C. D.
2.以下事件中属于必然事件的是〔 〕
A. 任意买一张电影票,座位号是偶数 B. 367人中至少有2人的生日相同
C. 掷一次骰子,向上的一面是5点 D. 某射击运发动射击1次,命中靶心
3.△ABC中,∠C=Rt∠,假设AC= ,BC=1,那么sinA的值是〔 〕
A. B. C. D.
4.如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,那么旗杆的高为〔 〕
A. 6m B. 8.8m C. 12m D. 15m
5.一个点到圆的最大距离为9 cm,最小距离为3 cm,那么圆的半径为〔 〕
A. 3 cm或6 cm B. 6 cm C. 12 cm D. 12 cm或6 cm
6.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,假设要使小长方形与原长方形相似,那么原长方形纸片的边a、b应满足的条件是〔 〕
A. a= b B. a=2b C. a=2 b D. a=4b
7.以下有关圆的一些结论:①弦的垂直平分线经过圆心;②平分弦的直径垂直于弦;③相等的圆心角所对的两条弦的弦心距相等;④等弧所在的扇形面积都相等,其中正确结论的个数是〔 〕
A. 4 B. 3 C. 2 D. 1
8.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形〞,那么半径为4的“等边扇形〞的面积为〔 〕
A. 8 B. 16 C. 2π D. 4π
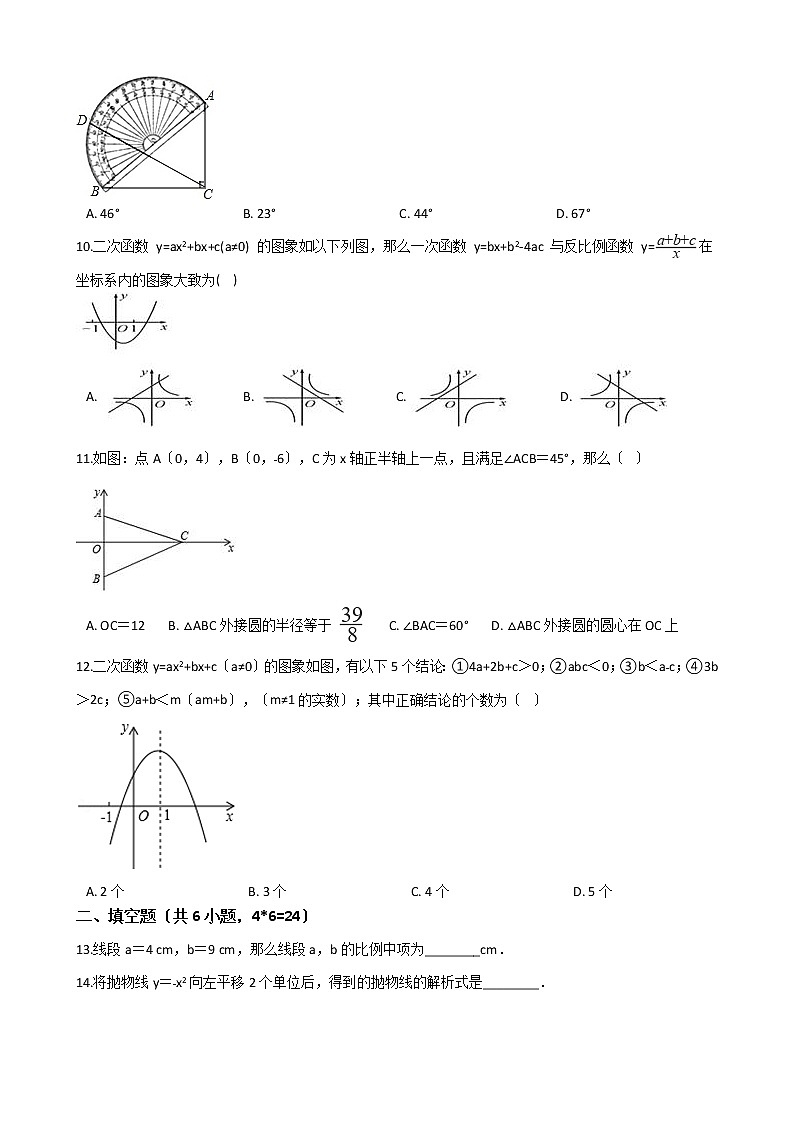
9.如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,那么∠ACD的度数为〔 〕
A. 46° B. 23° C. 44° D. 67°
10.二次函数 y=ax2+bx+c(a≠0) 的图象如以下列图,那么一次函数 y=bx+b2-4ac 与反比例函数 y=在坐标系内的图象大致为( )
A. B. C. D.
11.如图:点A〔0,4〕,B〔0,﹣6〕,C为x轴正半轴上一点,且满足∠ACB=45°,那么〔 〕
A. OC=12 B. △ABC外接圆的半径等于 C. ∠BAC=60° D. △ABC外接圆的圆心在OC上
12.二次函数y=ax2+bx+c〔a≠0〕的图象如图,有以下5个结论:①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;⑤a+b<m〔am+b〕,〔m≠1的实数〕;其中正确结论的个数为〔 〕
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题〔共6小题,4*6=24〕
13.线段a=4 cm,b=9 cm,那么线段a,b的比例中项为________cm.
14.将抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是________.
15.如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是________.
16.如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,假设AO=8,BC=12,EO= BE,那么线段OD=________,BE=________.
17.如图,在直线l上摆放着三个正三角形:△ABC、△HFG、△DCE,BC= CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1 , S2 , S3 , 假设S1+S3=20,那么S1=________,S2=________.
18.如图,在△ABC中,AB=AC=5cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1cm的速度运动〔不与点B,C重合〕,点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=________.
三、解答题〔共8小题,66分〕
19.
〔1〕计算: sin60°﹣ cos45°+tan230°;
〔2〕假设 = = ≠0,求 的值.
20.在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
〔1〕从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
〔2〕在〔1〕的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
21.如图,小山岗的斜坡AC的坡度是 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB〔结果取整数〕
〔〕.
22.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
〔1〕求证:AC2=AB•AD;
〔2〕求证:△AFD∽△CFE.
23.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.假设供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
〔1〕试确定月销售量y〔台〕与售价x〔元/台〕之间的函数关系式和自变量x的范围;
〔2〕当售价x〔元/台〕定为多少时,商场每月销售这种空气净化器所获得的利润w〔元〕最大?最大利润是多少?
24.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
〔1〕AB与AC的大小有什么关系?请说明理由;
〔2〕假设AB=8,∠BAC=45°,求:图中阴影局部的面积.
25.定义:在一个三角形中,假设存在两条边 x 和 y,使得 y = x2 ,那么称此三角形为“平方三角形〞,x 称为平方边.
〔1〕假设等边三角形为平方三角形,那么面积为 是________命题;
有一个角为 30°且有一条直角边为 2 的直角三角形是平方三角形〞是________命题;〔填“真〞或“假〞〕
〔2〕假设a,b,c 是平方三角形的三条边,平方边 a=2,假设三角形中存在一个角为 60°, 求 c 的值;
〔3〕如图,在△ABC 中,D 是 BC 上一点.
①假设∠CAD=∠B,CD=1,求证,△ABC 是平方三角形;
②假设∠C=90°,BD=1,AC=m,CD=n,求tan∠DAB.〔用含m,n的代数式表示〕
26.如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点〔A点在B点左侧〕,A〔﹣1, 0〕,B〔3,0〕,直线l与抛物线交于A,C两点,其中C点的横坐标为2.
〔1〕求抛物线的函数解析式;
〔2〕P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
〔3〕点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
答案解析局部
一、选择题〔共12小题,4*12=48〕
1.【解析】【解答】解:A、∵,
∴3y=2x,故A不符合题意;
B、∵,
∴xy=6,故B不符合题意;
A、∵,
∴3y=2x,故C不符合题意;
A、∵,
∴3x=2y,故D符合题意;
故答案为:D
【分析】利用比例的性质:两内项之积等于两外项之积,再对各选项逐一判断,可得比例式正确的选项。
2.【解析】【解答】解:A、任意买一张电影票,座位号是偶数,此事件是随机事件,故A不符合题意;
B、367人中至少有2人的生日相同,一年最多有366天,故此事件是必然事件,故B符合题意;
C、掷一次骰子,向上的一面是5点,此事件是随机事件,故C不符合题意;
D、某射击运发动射击1次,命中靶心,此事件是随机事件,故D不符合题意;
故答案为:B.
【分析】根据事件发生可能性的大小,在一定条件下,一定发生的事件是必然事件,不可能发生的事件是不可能事件,可能发生,也可能不发生的事件是随机事件,再对各选项逐一判断。
3.【解析】【解答】解:∵ Rt△ABC中,AC= ,BC=1
∴
∴sinA=.
故答案为:C.
【分析】利用勾股定理求出AB的长,再利用锐角三角函数的定义求出sinA的值。
4.【解析】【解答】解:如图
由题意可知DE∥BC,AE=8,EC=22,DE=3.2,
∴AC=AE+EC=8+22=30,
∴△ADE∽△ACB,
∴
∴
解之:BC=12
故答案为:C.
【分析】由题意可得到AE,EC,DE,AC的长,再由DE∥BC,可证得△ADE∽△ACB,然后利用相似三角形的对应边成比例,可求出BC的长。
5.【解析】【解答】解:当点P在圆O外时,
∵AP=9,PB=3
∴AB=AP-PB=9-3=6,
∴AO=6÷2=3cm;
当点P在圆O内时,
AP=9,BP=3
∴AB=9+3=12
∴圆的半径OA=12÷2=6cm,
∴圆的半径为3cm或6cm.
故答案为:A
【分析】分情况讨论:当点P在圆O外时;当点P在圆O内时,利用分别求出圆的直径,继而可求出圆的半径。
6.【解析】【解答】解:∵将长为a,宽为b的长方形纸片对折两次,
∴小长方形的长为b,宽为
∵原长方形和对折两次后的小长方形相似,
∴
解之:a=2b.
故答案为:B.
【分析】根据长为a,宽为b的长方形纸片对折两次,可得到小长方形的长和宽,再根据相似多边形的对应边成比例,即可得到a与b的数量关系。
7.【解析】【解答】解:弦的垂直平分经过圆心,故①正确;
平分弦〔不是直径〕的直径垂直于弦,故②错误;
在同圆或等圆中,相等的圆心角所对的两条弦的弦心距相等,故③错误;
等弧所在的扇形面积都相等,故④正确;
正确结论的序号为:①④.
故答案为:C.
【分析】利用垂径定理可对①②作出判断;再根据圆心角,弧,弦,弦心距定理的前提条件:在同圆或等圆中,可对③④作出判断;综上所述可得正确结论的个数。
8.【解析】【解答】解:∵扇形的弧长等于它的半径,当半径为4时,
∴此扇形的弧长为4,
∴此等边扇形〞的面积为.
故答案为:A.
【分析】根据 等边扇形〞的定义,可知扇形的半径和弧长都为4,再利用扇形的面积公式:S扇形=〔l为扇形的弧长,r为扇形的半径〕,代入计算可求解。
9.【解析】【解答】解:连接OD,
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,
∴点A,B,C,D共圆,
∵点D对应的刻度是46°,
∴∠BOD=46°,
∴∠BCD= ∠BOD=23°,
∴∠ACD=90°-∠BCD=67°.
故答案为:D.
【分析】连接OD,首先根据四点共圆的条件判断出点A,B,C,D共圆,根据同弧所对的圆周角等于圆心角的一半得出∠BCD= ∠BOD=23°,进而再根据角的和差,由∠ACD=90°-∠BCD即可算出答案.
10.【解析】【解答】解:∵抛物线的开口向上,对称轴在对称轴的右侧,
∴a>0,b<0,
抛物线与x轴有两个不同的交点,
∴b2-4ac>0
∴y=bx+b2-4ac的图像经过第一、二、四象限,故排除A,C.
当x=1时,a+b+c<0,
∴ 反比例函数 y=的图像分支在第二、四象限,排除B,
故答案为:D.
【分析】观察二次函数的图像,可知b,b2-4ac的大小,就可判定出一次函数的图像所经过的象限;再由x=1时可确定出a+b+c的大小,即可得出反比例函数图像分支的象限,综上所述,可得到答案。
11.【解析】【解答】解:作△ABC的外接圆M,过点M作MD⊥x轴于点D,过点M作MF⊥y轴于点F,连接AM,BM,CM,
∴AF=BF
∵点A〔0,4〕,点B〔0,-6〕
∴AB=4-〔-6〕=10
∴AF=5
∴OF=DM=1,
∵∠ACB=45°,
∴∠AMB=2∠ACB=90°,
在Rt△AMB中,AM=BM,MF⊥AB,
∴MF=AB=×10=5,
∴OD=5,
AM=MC=ABsin∠ABM=10×sin45°=.
在Rt△CDM中,
,
∴CO=DO+DC=5+7=12.
故答案为:A.
【分析】作△ABC的外接圆M,过点M作MD⊥x轴于点D,过点M作MF⊥y轴于点F,连接AM,BM,CM,利用垂径定理可知AF=BF,利用点A,B的坐标,可求出AF,OF、DM的长,再利用等腰直角三角形的性质,可求出MF的长,再利用解直角三角形求出AM,MC的长,然后利用勾股定理求出CD的长,根据CO=DO+DC,可求出CD的长。
12.【解析】【解答】解:∵抛物线的对称轴为直线x=1,抛物线的一个交点在-1和0之间,
∴抛物线的另一个交点在2和3之间,
∴当x=2时,y>0
∴4a+2b+c>0,故①正确;
∵由图像可知
抛物线开口向下,与y轴交于正半轴,对称轴在y轴的右侧,
a<0,c>0,b>0,
∴abc<0,故②正确;
∴a-b-c<0即b>a-c,故③错误;
∵对称轴为
∴
∵当x=-1时y<0
∴a-b+c<0
∴
∴2c<3b,即3b>2c,故④正确;
∵当x=1时,y=a+b+c的值最大,
当x=m〔m≠1〕时,y=m2a+bm+c
∴a+b+c>m2a+bm+c,即a+b>m〔am+b〕,故⑤错误;
正确结论的序号为:①②④.
故答案为:B.
【分析】观察函数图像,可知抛物线的对称轴为直线x=1,由此可得到抛物线与x轴的两交点坐标的取值范围,即可得到当x=2时,y>0,可对①作出判断;再观察抛物线的开口方向,对称轴,与y轴的交点坐标,可得到a,b,c的取值范围,从而可得到abc的符号,可对②作出判断;再确定出a-b-c的符号,可对③作出判断;当x=-1时y<0,结合对称轴可得到3b>2c,可对④作出判断;再利用二次函数的最值,可对⑤作出判断,综上所述可得到正确结论的个数。
二、填空题〔共6小题,4*6=24〕
13.【解析】【解答】解:设线段a,b的比例中项为x,
那么x2=ab=4×9=36,
解之:x=6.
故答案为:6.
【分析】根据x是a,b的比例中项,那么x2=ab,代入计算可求解。
14.【解析】【解答】解:抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式为y=-〔x+2〕2.
故答案为:y=-〔x+2〕2.
【分析】利用二次函数的平移规律:上加下减,左加右减,即可得出平移后的函数解析式。
15.【解析】【解答】解:点C的位置如图
由图形可知一共有7种结果,能是△ABC是直角三角形的有C1 , C2 , C3,C44种情况,
∴P〔△ABC是直角三角形〕=.
故答案为:.
【分析】根据题意在图形上标出点C的位置,可知所有等可能的结果数及能构造直角三角形的情况数,再利用概率公式进行计算可求解。
16.【解析】【解答】解:连接OB,
∵点O是BC的中点,
∴OD⊥BC,
∴BD=BC=×12=6
∵AO=BO=8,
∴;
设BE=x,那么DE=6-x,
∵ EO= BE
∴OE=
在Rt△ODE中,
∴
解之:x1=4,x2=-16〔舍去〕
∴BE=4
故答案为:;4.
【分析】 连接OB,利用垂径定理可求出BD的长,再利用勾股定理求出OD的长;设BE=x,用含x的代数式表示出DE,OE的长,再利用勾股定理建立关于x的方程,解方程求出x的值,即可得到BE的长。
17.【解析】【解答】解:如图,
∵△ABC、△HFG、△DCE都是正三角形,
∴∠ABC=∠HFG=∠DCE=60°,
∴GN∥DC∥HF∥AB,FM∥AC∥HG∥DE,F、G分别是BC、CE的中点,
∴点M,点P分别是AB,AC的中点,△BMP和△CPF是等边三角形,
∴CP=MF,
∴, CE=2CG=2GE,
∴
同理可证△CMG和△NGE是等边三角形,
∴CM=CG=GE=PH,
∴
∴S1=S2 , S2=3S2 ,
∵ S1+S3=20
∴S2+S2=20,
解之:S2=6,
∴S1=2.
故答案为:2;6.
【分析】根据题意易证S1 , S2 两个平行四边形的高相等,长是 S1的3倍,S3与S2的长相等,高是S3的, 再用含S2的代数式表示出 S1 , S3 , 然后根据S1+S3=20 ,建立方程求解即可。
18.【解析】【解答】解:如图1,当PA=PQ时,过点A作⊥BC于点F,过点P作PE⊥AC于点E,
∵△ABC是等腰三角形,
∴BF=CF=BC=4,∠B=∠C,
∵∠APQ+∠QPC=∠B+∠BAP,
∵∠APQ=∠B,
∴∠QPC=∠BAP,
∴△BAP∽△CPQ,
∴
∵点P在边BC上沿B到C的方向以每秒1cm的速度运动
∴BP=t,PC=8-t,
∴
解之:CQ=,
∴
∵AP=PQ,PE⊥AQ,
∴,
∴CE=EQ+CQ=
,
解之:t1=3,t2=13〔舍去〕;
如图2,当AQ=PQ,过点P作PH⊥AC于点H,
∴∠QAP=∠QPA=∠C,
∴AP=PC,
∴AH=CH=,
∵, PC=8-t,
∴
解之:.
故答案为:或3.
【分析】如图1,当PA=PQ时,过点A作⊥BC于点F,过点P作PE⊥AC于点E,利用等腰三角形的性质,可求出BF、CF的长,再证明∠QPC=∠BAP,利用有两组角对应相等的两三角形相似,可知△BAP∽△CPQ,根据相似三角形的对应边成比例,结合点的运动,可用含t的代数式表示出PC,BP,CQ,AQ的长,从而可表示出CE的长,然后根据锐角三角函数的定义,建立关于t的方程,解方程求出t的值;如图2当AQ=PQ,过点P作PH⊥AC于点H,利用等腰三角形的判定和性质,可证得AP=PC,从而可求出PH的长,在Rt△CPH中,利用锐角三角函数的定义,建立关于t的方程,解方程求出t的值,继而可得到符合题意的t的值。
三、解答题〔共8小题,66分〕
19.【解析】【分析】〔1〕先将特殊角的三角函数值代入,再利用二次根式的乘法法那么进行计算,然后合并即可。
〔2〕设, 用含k的代数式表示出x,y,z,再将x,y,z代入代数式化简即可。
20.【解析】【分析】〔1〕白球的个数与小球总数的比即为摸到白球的频率,据此列出方程即可求得n的值;
〔2〕用画树状图或者列表的方法,求出先后摸出两个球的所有等可能结果共有16种,其中摸出不同颜色的两个球的结果有10种,即可求出其概率。
21.【解析】【分析】利用坡度可得到BC与AB之间的数量关系,再利用锐角三角函数的定义,可得到AB与BD之间的数量关系,然后根据BD-BC=CD,建立关于AB的方程,解方程求出AB的值。
22.【解析】【分析】〔1〕利用角平分线可证得∠DAC=∠CAB,根据有两组对应角相等的两三角形相似,可证△ADC∽△ACB,再利用相似三角形的对应边成比例,可证得结论。
〔2〕根据直角三角形斜边上的中线等于斜边的一半,可得到CE=BE=AE,再证明∠DAC=∠ECA,利用平行线的性质,易证CE∥AD,然后可证得结论。
23.【解析】【分析】〔1〕抓住关键的条件:售价每降低10元,就可多售出50台。根据月销售量y=200+多售出的数量,列出y与x的函数解析式;再根据供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务,建立关于x不等式组,解不等式组求出x的取值范围。
〔2〕根据利润W=每一台的利润×销售量,列出W与x的函数解析式,再将函数解析式转化为顶点式,然后利用二次函数的性质即可求解。
24.【解析】【分析】〔1〕利用直径所对的圆周角是直角,可证得AD⊥BC,再由CD=BD,再利用垂直平分线的性质,可证得结论。
〔2〕连接OD、过D作DH⊥AB,利用等腰三角形的性质,可证得∠BAD=45°,再根据圆周角定理可证得△OBD是等腰直角三角形,再利用三角形的面积公式可求出△OBD的面积,再利用三角形的面积公式可求出扇形BOD的面积,然后利用扇形的面积减去三角形的面积。
25.【解析】【解答】解:〔1〕如图,△ABC是等边三角形,过点A作AD⊥BC于点D,
∵等边三角形为平方三角形,
∴AB=BC,∠B=60°
设边长为x,那么x=x2
解之:x=1,x=0〔舍去〕
∴AB=BC=1,
∴BD=,
∴AD=ADsin∠B=1×sin60°=
∴S△ABC=.
在Rt△ABC中,假设∠B=30°,AC=2,
∴AB=2AC=2×2=22=AC2 , 此时△ABC是“平方三角形〞;
当BC=2时,
cos∠B=
∴AB=
∴AC=
∴此时△ABC不是“平方三角形〞,故此命题为假命题.
故答案为:真;假.
【分析】〔1〕根据题意画出图形,利用等边三角形的性质和“平方三角形〞的定义,可得到△ABC的三边长及∠B的度数,再利用解直角三角形可求出AD的长,然后利用三角形的面积公式可求出此三角形的面积,即可作出判断;分情况讨论:30°所对的直角边为2时,此时可求出斜边的长,即可作出判断;当另一直角边为2时,求出三角形其它两边的长,根据三边长可作出判断。
〔2〕分情况讨论:当b=a2=4时,此时a,b两边的夹角为60°画出图形,利用勾股定理求出c的长;当c=a2=4时,假设a,c两边的夹角为60°,利用勾股定理求出c边上的高及另一直角边的长,再利用勾股定理及线段的和差求出c的值。
〔3〕①利用条件易证△CAD∽△CBA,利用相似三角形的对应边成比例,可证得AC2=CB·CD,从而可推出CA2=CB,即可证得结论;②延长CD至点E,使得∠E=∠DAB,连结AE,根据有两组对应角相等的三角形相似,利用相似三角形的对应边成比例可证得DA2=DB·DE,再由∠C=90°及AC=m,CD=n,可推出DA2=m2+n2 , 再用含m,n的代数式表示出DE的长,然后利用锐角三角函数的定义,可求出结果。
26.【解析】【分析】〔1〕将点A、B的坐标代入函数解析式,建立关于a,b的方程组,解方程组求出a,b的值,即可得到函数解析式。
〔2〕将点C的横坐标代入函数解析式求出y的值,可得到点C的坐标,再利用待定系数法求出直线AC的函数解析式,设点P的横坐标,可表示出点P,E的坐标,然后列出PE与x的函数解析式,利用二次函数的性质,可得出PE的最大值。
〔3〕①利用平行四边形的性质,可知AC∥GF,点C和点G的纵坐标互为相反数,将点C的纵坐标3代入函数解析式,建立关于x的方程,解方程求出x的值,可得到点G的坐标,再由GF∥AC及点G的坐标,可求出直线GF的解析式, 由y=0可求出对应的x的值,可得到点F的坐标,同理可求出符合题意的点F的其它的坐标。
2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案: 这是一份2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案,共12页。
2020-2021年浙江省宁波市九年级上学期数学第一次月考试卷及答案: 这是一份2020-2021年浙江省宁波市九年级上学期数学第一次月考试卷及答案,共14页。
2020-2021年浙江杭州拱墅区九年级上学期数学12月月考试卷及答案: 这是一份2020-2021年浙江杭州拱墅区九年级上学期数学12月月考试卷及答案,共12页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。












