2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案

这是一份2020-2021年浙江省杭州市六校九年级上学期数学12月月考试卷及答案，共12页。


九年级上学期数学12月月考试卷
一、选择题〔此题有10小题，每题3分，共30分〕
1.假设 ,那么 =  〔     〕
A. 3：2                                  B.   2：3                                  C.   2：1                                  D.   1：2
2.圆心角为 的弧长为 ，那么扇形的半径为〔     〕
A. 6                                        B.                                         C.   4                                        D.  
3.函数 的图象与坐标轴的交点个数是〔     〕
A. 0                                         B.   1                                         C.   2                                         D.   3
4.⊙O的半径为5，点 的坐标为〔-1,0〕，点 的坐标为〔-3,4〕，那么点 与⊙O的位置关系是〔     〕
A. 点P在⊙O的外                   B. 点P在⊙O的上                   C. 点P在⊙O的内                   D. 不能确定
5.某校举行以“我为词霸〞为主题的英语单词比赛．决赛阶段只剩下甲,乙,丙,丁四名同学，那么甲.乙同学获得前两名的概率是 〔     〕
A.                                          B.                                          C.                                          D. 
6.抛物线 经变换后得到抛物线 ，那么这个变换可以是〔     〕
A. 向左平移2个单位           B. 向右平移2个单位           C. 向左平移5个单位           D. 向右平移5个单位
7.A，B，C在⊙O上，△ABO为正三角形，那么 〔     〕
A. 150°                             B. 120°                             C. 150°或 30°                             D. 120°或 60°
8.如图，假设△ 中， ， ， 是 的中点， ， ，那么点 到边 的距离是 〔     〕

A. 4                                          B. 6                                          C. 8                                          D.   12
9.抛物线 经过 , ，且 ，那么以下不等式中一定成立的是   〔     〕
A.                     B.                     C.                     D. 
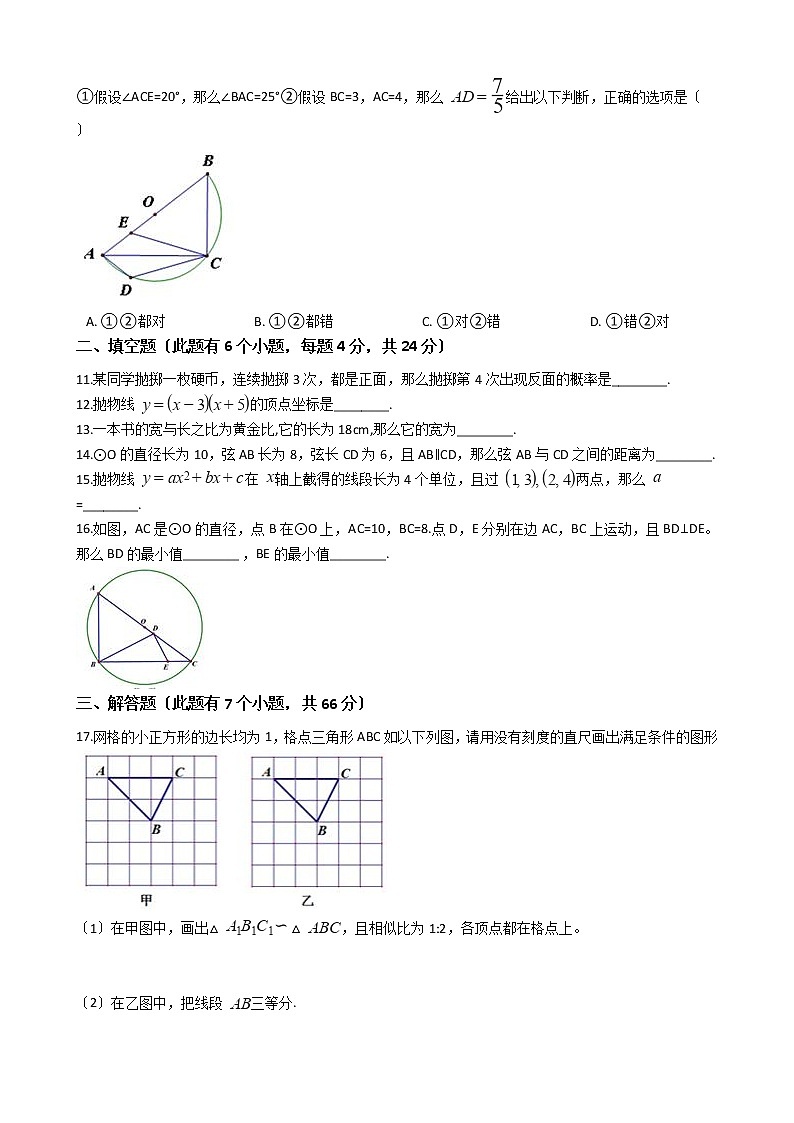
10.如图，在Rt△ABC中，∠ACB=90°，以AB为直径作半圆。点D在弧 上〔不与A，C重合〕，点E在AB上，且点D.E关于AC对称. 给出以下结论：
①假设∠ACE=20°，那么∠BAC=25°②假设BC=3，AC=4，那么 给出以下判断，正确的选项是〔    〕

A. ①②都对                           B. ①②都错                           C. ①对②错                           D. ①错②对
二、填空题〔此题有6个小题，每题4分，共24分〕
11.某同学抛掷一枚硬币，连续抛掷3次，都是正面，那么抛掷第4次出现反面的概率是________.
12.抛物线 的顶点坐标是________.
13.一本书的宽与长之比为黄金比,它的长为18cm,那么它的宽为________.
14.⊙O的直径长为10，弦AB长为8，弦长CD为6，且AB∥CD，那么弦AB与CD之间的距离为________.
15.抛物线 在 轴上截得的线段长为4个单位，且过 两点，那么 =________.
16.如图，AC是⊙O的直径，点B在⊙O上，AC=10，BC=8.点D，E分别在边AC，BC上运动，且BD⊥DE。那么BD的最小值________ ，BE的最小值________.

三、解答题〔此题有7个小题，共66分〕
17.网格的小正方形的边长均为1，格点三角形ABC如以下列图，请用没有刻度的直尺画出满足条件的图形

〔1〕在甲图中，画出△ △ ，且相似比为1:2，各顶点都在格点上。


〔2〕在乙图中，把线段 三等分.

18.四张小卡片上分别写有数字-1,1,2,3，它们除数字外没有任何区别，现将它们放在盒子里搅匀．
〔1〕随机地从盒子里抽取一张，求抽到数字2的概率；
〔2〕随机地从盒子里抽取一张，将数字记为 ，不放回再抽取第二张，将数字记为 ，请你用画树状图或列表的方法表示所有等可能的结果，并求出点 在函数 图象上的概率．
19.如图，在平行四边形ABCD中，EF∥AB.

〔1〕写出所有相似三角形;
〔2〕假设 ， ，求 的长.
20.菱形的的两条对角线分别为 与 ，设菱形的面积为 .
〔1〕求y关于x的函数表达式，请写出自变量的取值范围；
〔2〕判断命题“当面积取到最大值时，此菱形为正方形〞是真命题还是假命题？请说明理由.
21.如图，⊙O是△ABC的外接圆，AB=AC，D是优弧BC上的一个动点，连结AD交BC于点E，连结BD.

〔1〕假设AE=2，DE=8，求AC的长;
〔2〕假设D是优弧BC上中点时，求证： .
22.二次函数 的图象经过三点〔1，0〕，〔-3，0〕，〔0， 〕.
〔1〕求该二次函数的解析式；
〔2〕假设反比例函数 图像与二次函数 的图像在第一象限内交于点 , 落在两个相邻的正整数之间，请写出这两个相邻的正整数；
〔3〕假设反比例函数 的图像与二次函数 的图像在第一象限内的交点为A，点A的横坐标为 满足 ，试求实数 的取值范围。
23.如图，在菱形ABCD中， ， ,点E是边BC的中点，连接DE,AE.

〔1〕求DE的长；
〔2〕点F为边CD上的一点，连接AF，交DE于点G，连接EF，假设 ,
①求证：△ △ ；
②求DF的长.

答案解析局部
一、选择题〔此题有10小题，每题3分，共30分〕
1.【解析】【解答】解：∵a=2b，∴a∶b=2b∶b=2∶1.
故答案为：C.
【分析】将a=2b代入a∶b就可算出答案.
2.【解析】【解答】解：设该扇形的半径为r，由题意
得   ，
解得  r=.
故答案为：.
【分析】根据弧长的计算公式列出方程，求解即可.
3.【解析】【解答】解：∵ 函数 中a=1＞0，
∴图象开口向上，
又∵该函数与y轴交点的坐标为〔0,1〕，
∴ 函数 的图象与坐标轴的交点个数是 1.
故答案为：B.
【分析】根据函数图象的开口方向及与y轴交点坐标即可判断得出答案.
4.【解析】【解答】解：∵ 点 的坐标为〔-1,0〕，点 的坐标为〔-3,4〕 ，
∴OP=，
又∵＜5，
∴点P在⊙O的内 .
故答案为：C.
【分析】根据两点间的距离公式算出OP的长，由于OP的长小于该圆的半径，故该点在圆内.
5.【解析】【解答】解：根据题意画出树状图：

由图可知：共有12种等可能的结果数，其中甲、乙恰好是第一名和第二名的结果数为2，

所以甲、乙恰好是第一名和第二名的概率=.
故答案为：D.
【分析】根据题意画出树状图，由图可知：共有12种等可能的结果数，其中甲、乙恰好是第一名和第二名的结果数为2，根据概率公式即可算出答案.
6.【解析】【解答】解：∵  =〔x+1〕2-4,∴其顶点坐标为：〔-1,4〕，
∵ =〔x-1〕2-4,∴其顶点坐标为：〔1,4〕，
∴ 抛物线 向右平移2个单位得到 抛物线 .
故答案为：B.
【分析】首先将各个抛物线的解析式配成顶点式得出其顶点坐标，然后根据点的坐标的平移规律“左减右加〞即可判断得出答案.
7.【解析】【解答】解：∵△ABO为正三角形，∴∠AOB=60°，当点C在优弧上的时候，∠ACB=∠AOB=30°，当点C在劣弧AB上的时候，∠ACB=180°-30°=150°，∴∠ACB的度数为 150°或 30° .
故答案为：C.
【分析】根据等边三角形的性质得出∠AOB的度数，然后分当点C在优弧上的时候与当点C在劣弧AB上的时候两种情况，根据同弧所对的圆周角等于圆心角的一半得出答案.
8.【解析】【解答】解：如图：过点F作FN⊥BC于点点N，过点G作GH⊥BC于点H，过点F作FM⊥AB于点M交FM于点O，

∵ ，
∴∠ADE=∠B=90°，
∵FM⊥AB，∴∠FMB=90°，
∴∠FMB=∠ADE=∠B=90°，
∴DE∥FM∥BC，
∴,
∴DM=BM=6,
∵FN⊥BC，FM⊥AB，
∴∠FNBB=90°，∠FMB=90°，
又∵∠B=90°，
∴四边形FNBM是矩形，
∴FN=BM=6，
∵GH⊥BC，∠B=90°，
∴GH∥BD，
∴,
即,
∴GO=2，
∴GH=GO+OH=8.
故答案为：C.
【分析】首先推出DE∥FM∥BC，根据平行线分线段成比例定理得出， 故DM=BM=6,然后再推出GH∥BD，根据平行线分线段成比例得出， 故GO=2，接着判断出四边形FNBM是矩形，根据矩形的对边相等得出FN=BM=6，最后根据线段的和差即可得出答案.
9.【解析】【解答】解：①a>0时，二次函数图象开口向上，

∵|x1+1|＜|x2+1|,

∴y1＜y2 ，

∴a(y1−y2)＜0，

②a<0时，二次函数图象开口向下，

∵|x1+1|＜|x2+1|,

∴y1＞y2 ，

∴a(y1−y2)＜0，

综上所述,表达式正确的选项是 .
故答案为：B.
【分析】由于函数的对称轴直线是x=-1，分①a>0时与②a<0时两种情况，根据二次函数的对称性判断出y1与y2的大小，进而即可一一判断得出答案.
10.【解析】【解答】解：连接OC、BD，如图：

两线相交于点F.∵ 点D.E关于AC对称 ，
∴AC是的DE的垂直平分线，
∴AE=AD,CE=CD，
又∵AC=AC
∴△ADC≌△AEC，
∴∠ACE=∠ACD=20°，∠BAC=∠DAC，
∵AB是圆的直径，
∴∠ACB=90°，
∴∠BCD=∠BCA+∠ACD=110°，
∵四边形ABCD是圆的内接四边形，
∴∠BAC=180°-∠BCD=70°，
∴ ∠BAC =∠DAC=35°，故①错误；
在Rt△ABC中，∠ACB=90°， BC=3，AC=4 ，
∴AB=5，∴OB=OC=2.5，
∵∠DBC =∠DAC=35°，
∴BC=CD=3，弧BC=弧CD，
∴OC⊥BD，∴∠BFO=90°，设OF=x,
根据勾股定理得出OB2-OF2=BC2-CF2 ，
2-x2=32-〔〕2 ， 解得x=，
∵AB是圆的直径，∴∠BDA=90°，由∵OC⊥BD，∴∠OFB=90°=∠ADB，∴OC∥AD，∵点O是AB的中点，∴AD=2OF=,故②正确.
故答案为：D.
【分析】根据轴对称的性质及三角形全等的判断方法判断出△ADC≌△AEC，根据全等三角形的对应角相等得出∠ACE=∠ACD=20°，∠BAC=∠DAC，根据直径所对圆周角是直角及圆内接四边形的对角互补得出∠BAC=70°，从而得出∠BAC =∠DAC=35°，根据圆周角定理得出弧BC=弧CD，从而根据垂径定理得出OC⊥BD，然后根据勾股定理，由OB2-OF2=BC2-CF2 ， 建立方程，求解算出OF的长，进而再根据三角形的中位线定理得出AD的长.
二、填空题〔此题有6个小题，每题4分，共24分〕
11.【解析】【解答】解：∵抛掷一枚质地均匀的硬币一次，可能的结果有：正面向上，反面向上，
∴P〔正面向上〕=．
故答案为：．
【分析】每一次抛掷硬币都是独立的一次，不受前面任何一次抛掷的结果的影响，而抛掷一枚质地均匀的硬币一次，可能的结果有：正面向上，反面向上；直接利用概率公式求解即可求得答案．
12.【解析】【解答】解： ∵=x2+2x-15=x2+2x+1-16=(x+1)2-16,
∴该函数的顶点坐标为〔-1，-16〕.
故答案为：(-1,-16).
【分析】将解析式整理成一般形式，再利用配方法配成顶点式，即可得出其顶点坐标.
13.【解析】【解答】解：设该长方形的宽为xcm，
根据题意 得， 解得x= .
故答案为： .
【分析】由于黄金比的值， 故根据宽与长之比为黄金比列出方程，求解即可.
14.【解析】【解答】解：如图：分类讨论：

①当两条弦位于圆心O一侧时，如图1所示，

过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，

∵AB∥CD，

∴OE⊥AB，

∴E、F分别为CD、AB的中点，

∴CE=DE=CD=4，AF=BF=AB=3，

在Rt△AOF中，OA=5，AF=4，根据勾股定理得：OF=3，

在Rt△COE中，OC=5，CE=3，根据勾股定理得：OE═4，

那么EF=OE－OF=4－3=1；

②当两条弦位于圆心O两侧时，如图2所示，

同理可得EF=4＋3=7，

综上，弦AB与CD的距离为7或1．

故答案为：7或1．
【分析】分类讨论：当两条弦位于圆心O一侧时，如图1所示，过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，由AB∥CD，得出OE⊥AB，根据垂径定理得出E、F分别为CD、AB的中点，然后利用勾股定理分别算出OF、OE的长，进而根据EF=OE－OF算出答案；②当两条弦位于圆心O两侧时，如图2所示，同理求出OF、OE的长，进而根据EF=OE+OF算出答案，综上所述即可得出答案.
15.【解析】【解答】解：由题意可知：
解得：或.
故答案为： .
【分析】将点 代入 抛物线 得出两个方程，再根据抛物线在x轴上截得的线段长为4，列出第三个方程，然后解这三个方程组成的方程组即可求出a的值.
16.【解析】【解答】解：〔1〕当BD⊥AC时，BD取得最小值，
∵AC=10,BC=8,∠ABC=90°，
∴AB=,
∵S△ABC=,
∴6×8=10×BD，
∴BD=4.8；
〔2〕在Rt△BDE中，取BE的中点F，连接DF，那么DF=BE，以BE为直径作圆，当DF最小的时候那么BE最小，当DF⊥AC的时候，DF最小，此时△DFC∽△ABC，
∴， 即,DF=3，
∴BE的最小值为6.
故答案为：BD的最小值为4.8；BE的最小值为6.
【分析】〔1〕根据勾股定理算出AB的长，然后根据三角形的面积法即可算出BD的长；
〔2〕在Rt△BDE中，取BE的中点F，连接DF，那么DF=BE，以BE为直径作圆，当DF最小的时候那么BE最小，当DF⊥AC的时候，DF最小，此时△DFC∽△ABC，根据相似三角形对应边成比例列出方程，求解得出DF的长，进而即可得出答案.
三、解答题〔此题有7个小题，共66分〕
17.【解析】【分析】〔1〕利用方格纸的特点及勾股定理分别得出AB,AC,BC的长，进而根据相似三角形的对应边的比等于相似比且相似比为1∶2得出A1B1、A1C1,B1C1的长，从而再根据格点三角形的定义即可作出图形；
〔2〕利用平行线等分线段定理即可作出AB的三等分点M、N.
18.【解析】【分析】〔1〕盒子中共有4张没有任何区别的小卡片，从中随机的抽出一张，共有4种等可能的结果，而能抽到3的只有一种等可能的结果，根据概率公式即可算出答案；
〔2〕根据题意画出树状图，由图可知：等可能的情况数有12种，其中在 函数 图象上3种，根据概率公式即可算出答案.
19.【解析】【分析】〔1〕根据平行四边形的性质得出AB∥CD，∠C=∠A，根据二直线平行，内错角相等得出∠CDB=∠ABD，从而推出△DAB∽△BCD，根据平行于三角形一边的直线截其它两边，所截的三角形与原三角形相似，由EF∥AB ，得出 △DEF∽△DAB ，故△DEF∽△DAB∽△BCD ；
〔2〕根据相似三角形对应边成比例，由△DEF∽△DAB得出,根据比例式即可求出AB的长，进而根据平行四边形的对边相等得出CD的长.
20.【解析】【分析】〔1〕根据菱形的面积等于两对角线乘积的一半即可建立出y与x的函数关系式，根据x的取值要保证两对角线都不能为负数即可求出x的取值范围；
〔2〕此命题是假命题，理由如下：首先根据顶点坐标公式求出抛物线的顶点横坐标，并求出此时菱形两对角线的长度，根据对角线相等的菱形是正方形即可判断得出结论.
21.【解析】【分析】〔1〕根据等边对等角得出∠C=∠ABC，再根据同弧所对的圆周角相等得出∠C=∠D，故∠D=∠ABC，从而可以判断出△BAE∽△DAB，根据相似三角形对应边成比例得出AB2=AE×AD，从而即可求出答案；
〔2〕首先根据弧、弦、圆心角的关系得出AD是圆O的直径，根据垂径定理得出AD⊥BE，BE=BC，然后判断出△BEA∽△DEB，根据相似三角形对应边成比例得出BE2=DE×AE，从而即可得出答案.
22.【解析】【分析】〔1〕利用待定系数法即可求出抛物线的解析式；
〔2〕解联立反比例函数的解析式与抛物线的解析式组成的方程组求出其在第一象限内的交点的坐标，即可得出答案；
〔3〕根据抛物线的性质得出当2＜x＜3时，y1随着x增大而增大，对y2= 〔k＞0〕，y2随着X的增大而减小。因为A〔X0 ， Y0〕为二次函数图像与反比例函数图像的交点，所以当X0=2时，由反比例函数图象在二次函数上方得y2＞y1， 当X0=3时，由二次函数数图象在反比例上方得y1＞y2 ， 从而列出不等式组，求解即可.

23.【解析】【分析】〔1〕 连结BD ，根据菱形的性质及等边三角形的判定方法首先判定出△CDB是等边三角形，根据等边三角形的性质得出DE⊥BC，CE=2，然后利用勾股定理算出DE的长；
〔2〕①首先判断出△AGD∽△EGF，根据相似三角形对应边成比例得出， 又∠AGE=∠DGF，故△AGE∽△DGF；
②根据相似三角形的性质及含30°直角三角形的边之间的关系及勾股定理得出EF的长，然后过点E作EH⊥DC于点H，在Rt△ECH中，利用勾股定理算出FH的长，从而根据线段的和差即可算出答案.