鲁教版 (五四制)九年级上册4 解直角三角形教学演示课件ppt

这是一份鲁教版 (五四制)九年级上册4 解直角三角形教学演示课件ppt，共39页。PPT课件主要包含了在Rt△ABC中，你发现了什么，一角一边，议一议，解在Rt△ABC中，a2+b2c2，两条边或一边一角，解直角三角形，化未知为已知，即∠EBD30°等内容，欢迎下载使用。
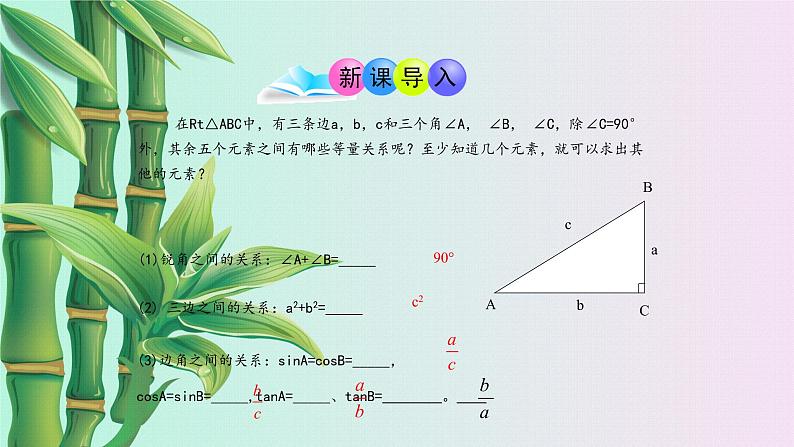
(2) 三边之间的关系：a2+b2=_____
(1)锐角之间的关系：∠A+∠B=_____
(3)边角之间的关系：sinA=csB=_____，csA=sinB=_____,tanA=_____、tanB= 。
在Rt△ABC中，有三条边a，b，c和三个角∠A， ∠B， ∠C，除∠C=90°外，其余五个元素之间有哪些等量关系呢？至少知道几个元素，就可以求出其他的元素？
利用计算器可得
根据以上条件可以求出塔身中心线与垂直中心线的夹角。你愿意试着计算一下吗？
如图设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C，在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m。
将上述问题推广到一般情形，就是：已知直角三角形的斜边和一条直角边，求它的锐角的度数。
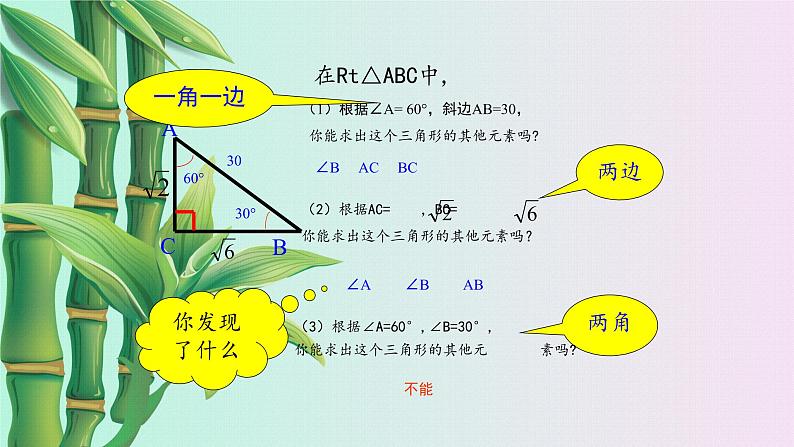
（1）根据∠A= 60°，斜边AB=30，
∠B AC BC
∠A ∠B AB
（3）根据∠A=60°,∠B=30°,你能求出这个三角形的其他元 素吗?
你能求出这个三角形的其他元素吗?
在直角三角形的六个元素中，除直角外，如果知道两个元素(其中至少有一个是边)，就可以求出其余三个元素。
在直角三角形中，由已知元素求未知元素的过程，叫解直角三角形。
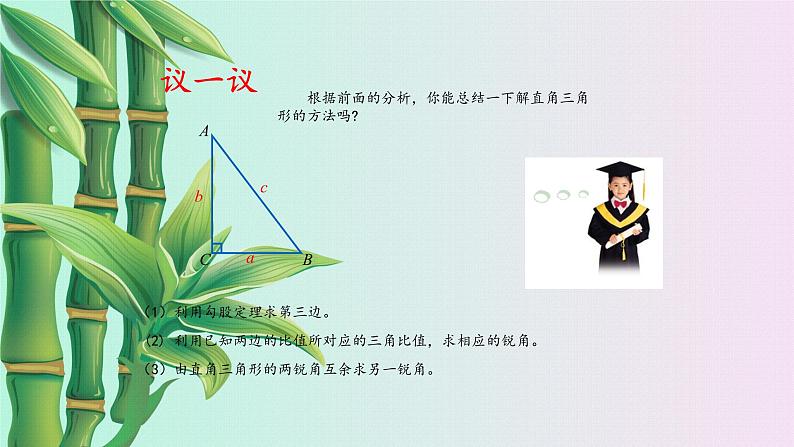
（1）利用勾股定理求第三边。 (2) 利用已知两边的比值所对应的三角比值，求相应的锐角。（3）由直角三角形的两锐角互余求另一锐角。
根据前面的分析，你能总结一下解直角三角形的方法吗?
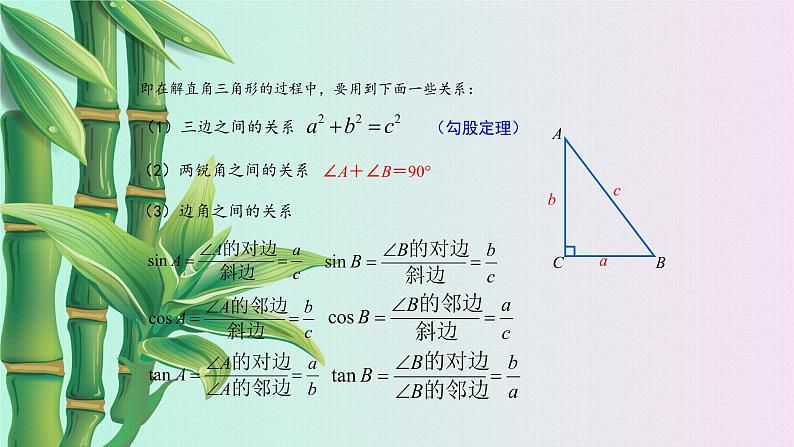
（2）两锐角之间的关系
（1）三边之间的关系
即在解直角三角形的过程中，要用到下面一些关系：
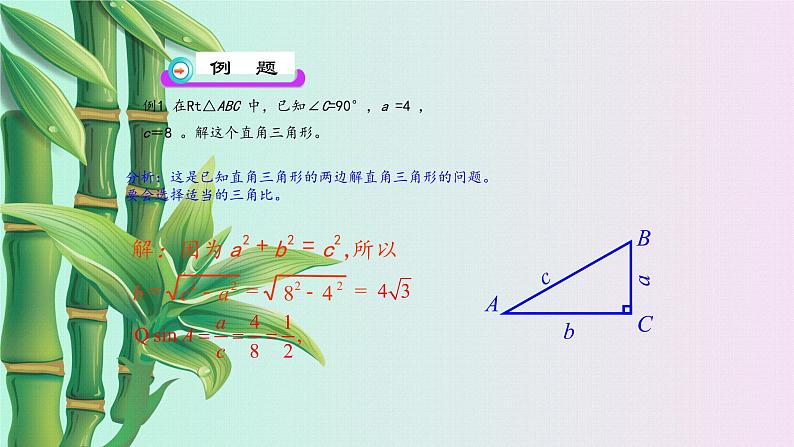
例1 在Rt△ABC 中，已知∠C=90°，a =4 ，c＝8 。解这个直角三角形。
分析：这是已知直角三角形的两边解直角三角形的问题。要会选择适当的三角比。
例2 在Rt△ABC 中，已知∠C=90°，a =35 ，b＝28。求∠A，∠B的度数（结果精确到1°）和c的长（结果保留两位有效数字）。
解：在Rt △ABC 中，
在Rt△ABC 中，∠C=90°。
（1）已知a，b，怎样求∠A的度数?
（2）已知a，c，怎样求∠A的度数?
（3）已知b，c，怎样求∠A的度数?
由此你能总结一下已知两边解直角三角形的方法吗?与同伴进行交流。
（1）已知c=26，b=24，求a的长和∠B的度数（结果精确到1`）；（2）已知a=5， ，求c和∠A，∠B的度数。
1.在下列直角三角形中不能求解的是（ ）(A)已知一直角边一锐角(B)已知一斜边一锐角(C)已知两边(D)已知两角
2.如图，在Rt△ABC中，∠C＝90°，解这个直角三角形。
课本习题2.6 1、2、3
上节课我们已经学过： 在直角三角形中，已知三边中的两边，求某个角的度数，下面我们来学习已知一条边与一个角，解直角三角形。
例3 在Rt△ABC中，已知∠C=90°，c=128，∠B=60°，解这个直角三角形。
例4 在Rt△ABC中，已知∠C=90°，a=15， 求∠B的度数和b，c的长（结果精确到1）。
（1）已知c， ∠A ，写出求a和b的式子；
（2）已知b， ∠A ，写出求a和c的式子；
（3）已知a， ∠A ，写出求b和c的式子；
由此你能总结一下已知一条边和一个锐角解直角三角形的方法吗?与同伴进行交流。
如图，在Rt△ABC中，∠B＝35°，b=20，解这个直角三角形（精确到0.1）
你还有其他方法求出c 吗?
（江西中考）如图，从点C测得树的顶角为33°，BC＝20米，则树高AB＝ 米（用计算器计算，结果精确到0.1米）
AB=BC·tanC=20×tan33°=13.0
课本习题2.7 1、2
1.直角三角形中元素之间的关系
（1）两锐角之间的关系:
∠A+ ∠ B=90°
（2）三边之间的关系:
（3）边角之间的关系：
2.在直角三角形中，由已知的 ，求出另一些 的过程，叫做 。
3.如果知道直角三角形的几个元素就可以求其他的元素？有几种情况？
两个元素（至少一个是边）
求下列各直角三角形中字母的值。
上节课我们已经学过：1.已知两边解直角三角形。2.已知一条边和一个锐角解直角三角形。
想一想：如果已知条件中，没有直接给出直角三角形，你会怎么办？
例5.如图，在△ABC中，已知∠A﹦60°，∠B﹦45°，AC﹦12，求AB的长。
转化思想：作AB边上的高，把锐角三角形转化为直角三角形，把问题转化为解直角三角形！
解：过点C作CD⊥AB，垂足为点D。
1.如图，在△ABC中，已知AB=5，AC=7，∠B=60°，求BC的长。
2.在等腰三角形∆ABC中，AB=AC，且一腰长与底边的比是5：8，求sinA，csB的值。
例6.如图，在△ABC中，∠B=47°，∠ACB=15°，AC=6，求AB的长（结果精确到0.01）。
解：过点C作CD⊥AB，与BA的延长线相交于点D。
∵ ∠B=47°，∠ACB=15°
∴ ∠CAD=∠B+∠ACB=47°+15°=62°
在Rt△ABC中，AC=6，∠CAD=62°，
在Rt△ABC中，∠B=47°，
解：过点B作BE⊥AC于点E；
∵ AB=AC，∠BAE=80°
∴ ∠ABC=∠ACB=40°
∠ABD=20°，∠ABE=10°
已知在△ABC中，AB+AC=9cm，AB和AC的夹角为30°，设当AB为x（cm）时，△ABC的面积为S（cm2）
（1）求S关于x的函数解析式；
（2）问何时△ABC的面积最大？最大面积为多少？
如果图中无直角三角形，可适当地作垂线等辅助线，“化斜为直”，“善于转化”为解直角三角形问题。
【化斜为直】，【善于转化】
四个解直角三角形的典型变式图形