





鲁教版 (五四制)九年级上册5 三角函数的应用教课内容课件ppt
展开了解仰角、俯角、方位角的概念,能应用解直角三角形解决一类观测实际问题。
进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角形中元素之间的关系。
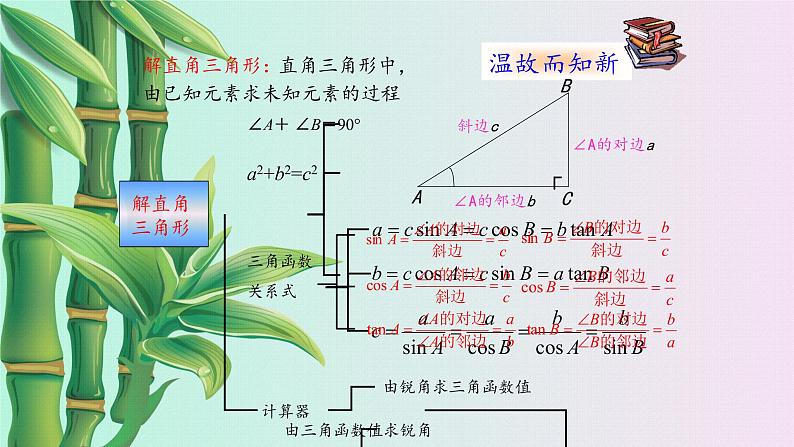
由已知元素求未知元素的过程
(1)有角先求角,无角先求边。
(2)有斜用弦,无斜用切;
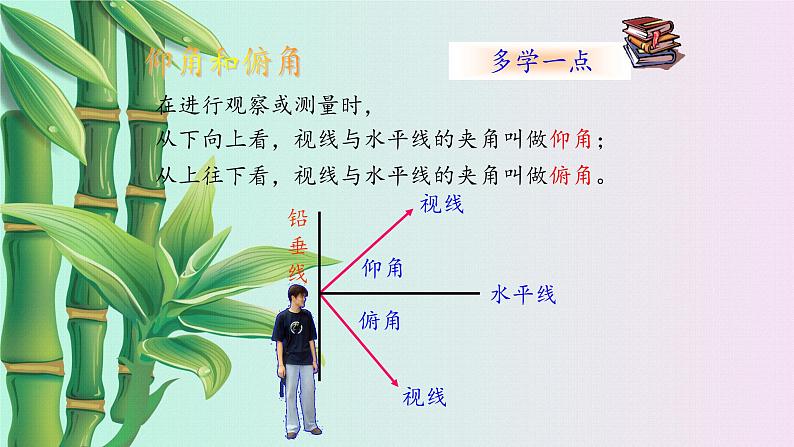
从上往下看,视线与水平线的夹角叫做俯角。
从下向上看,视线与水平线的夹角叫做仰角;
如图,小明想测量塔CD的高度。他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处。测得仰角为60°,小明的身高1.5 m。那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?
海中有一个小岛A,该岛四周10海里内有暗礁。今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流。
某商场准备改善原有楼梯的安全性能,楼梯的倾斜角由40º降为35º,已知原楼梯长为4米,(1)调整后楼梯会加长多少?(2)调整后楼梯会多占多少一段地面?(精确到0.01m)
请同学们自己画出图形,并解决问题,完成后与同伴交流。
通过作高转化为直角三角形
1.把实际问题转化成数学问题,这个转化包括两个方面:一是将实际问题的图形转化为几何图形,画出正确的示意图;二是将已知条件转化为示意图中的边、角或它们之间的关系。
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。
2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留)。
1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )A.由楼顶望塔顶仰角为60°B.由楼顶望塔基俯角为60°C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°
3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留)。
4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 (根号保留)。
求图中避雷针的长度(结果精确到0.01m)。
解:如图,根据题意,可知AB=20m,∠CAB=50°,∠DAB=56°
在Rt△DBA中,DB=ABtan56° ≈20×1.4826 =29.652(m);
在Rt△CBA中,CB=ABtan50° ≈ 20×1.1918 =23.836(m)
所以避雷针的长度DC=DB-CB=29.652-23.836≈5.82(m)。
必做题:书本练习1、2题。选做题:1.一架直升机从某塔顶A测得地面C、D两点的俯角分别为30°、45°,若C、D与塔底B共线,CD=200米,求塔高AB?2.有一块三形场地ABC,测得其中AB边长为60米,AC边长50米,∠ABC=30°,试求出这个三角形场地的面积。
3.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为5米,点D、B、C 在同一水平地面上。(1)改善后滑滑板会加长多少?(精确到0.01)(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由 (参考数据: )
1.理解坡度、坡角等概念,会应用解直角三角形的知识解决与坡度、坡角有关的问题。2.进一步培养分析、解决问题的能力,体会数形结合的思想。
同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:
水库大坝的横断面是梯形ABCD,坝顶DC=6m,坝高22m,斜坡AD的坡比为1∶3,斜坡BC的坡比为1∶2.5,求斜坡AD的坡面角α,坝底宽AB和斜坡AD的长(精确到0.1m)。
如图,某学校教学楼后面紧邻着一个山坡,坡上面是一块平地,BC∥AD,BE⊥AD,斜坡AB长26m,坡脚∠BAD=68°。为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造。经地质人员勘测,当坡脚不超过50°时,可确保山体不滑坡。
如果改造时保持坡脚A不动,坡顶B沿BC左移11m到F点处,这样改造能确保山体不滑坡吗?
1.一段河坝的横断面为等腰梯形ABCD,试根据下图中的数据求出坡角α和坝底宽AD。(单位是米,结果保留根号)
2.水库拦水坝的横断面为梯形ABCD,背水坡CD的坡比i=1:已知背水坡的坡长CD=24m,求背水坡的坡角α及拦水坝的高度。
解:过D作DE⊥BC于E
在Rt△DCE中,DE⊥BC,DC=24m
∴∠DCE=30°,∴DE=12(m).
故背水坡的坡角为30°,拦水坝的高度为12m。
3.为了灌溉农田,某乡利用一土堤修筑一条渠道,在堤中间挖出深为1.2m,下底宽为2m,坡度为1:0.6的渠道(其横断面为等腰梯形),并把挖出的土堆在两旁,使土堤的高度比原来增加了0.6m,如图所示,求:(1)渠面宽EF;(2)修400m长的渠道需挖的土方数。
用解直角三角形的知识解决实际问题的一般步骤:(1)审题,通过图形(题目没画出图形的,可自己画出示意图),弄清已知和未知;(2)找出有关的直角三角形,或通过作辅助线产生有关的直角三角形,把问题转化为解直角三角形的问题;(3)根据直角三角形元素(边、角)之间关系解有关的直角三角形。
习题2.10 1、2、3
数学九年级上册5 三角函数的应用优质课件ppt: 这是一份数学九年级上册5 三角函数的应用优质课件ppt,文件包含鲁教版五四制数学九上《三角函数的应用2》课件ppt、鲁教版五四制数学九上《三角函数的应用2》教案doc等2份课件配套教学资源,其中PPT共9页, 欢迎下载使用。
初中数学鲁教版 (五四制)九年级上册5 三角函数的应用完整版课件ppt: 这是一份初中数学鲁教版 (五四制)九年级上册5 三角函数的应用完整版课件ppt,文件包含鲁教版五四制数学九上《三角函数的应用1》课件ppt、鲁教版五四制数学九上《三角函数的应用1》教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
初中数学鲁教版 (五四制)九年级上册第二章 直角三角形的边角关系5 三角函数的应用背景图课件ppt: 这是一份初中数学鲁教版 (五四制)九年级上册第二章 直角三角形的边角关系5 三角函数的应用背景图课件ppt,共17页。PPT课件主要包含了教学目标,新课导入,想一想,解由题意可知,∠BAC18°,坡度的定义,坡角的定义,坡度的表达形式,课堂小结等内容,欢迎下载使用。













