2018年青岛市平度市中考一模数学试卷

这是一份2018年青岛市平度市中考一模数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
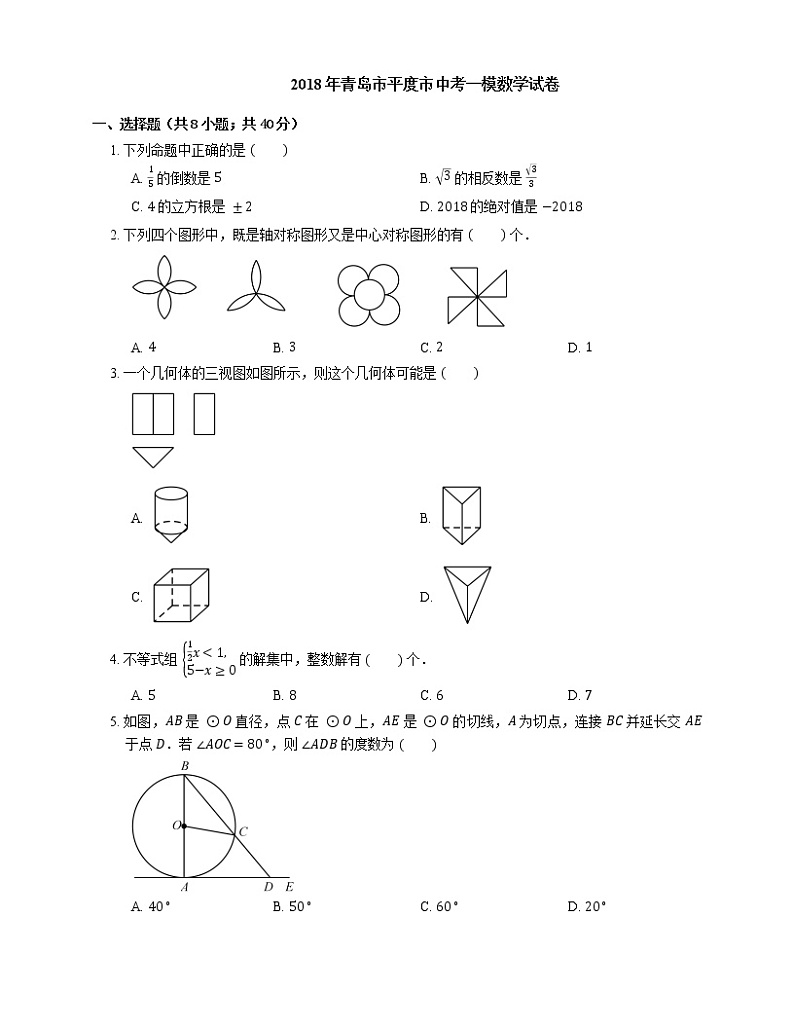
1. 下列命题中正确的是
A. 15 的倒数是 5B. 3 的相反数是 33
C. 4 的立方根是 ±2D. 2018 的绝对值是 −2018

2. 下列四个图形中，既是轴对称图形又是中心对称图形的有 个．
A. 4B. 3C. 2D. 1

3. 一个几何体的三视图如图所示，则这个几何体可能是
A. B.
C. D.

4. 不等式组 12x<1,5−x≥0 的解集中，整数解有 个．
A. 5B. 8C. 6D. 7

5. 如图，AB 是 ⊙O 直径，点 C 在 ⊙O 上，AE 是 ⊙O 的切线，A 为切点，连接 BC 并延长交 AE 于点 D．若 ∠AOC=80∘，则 ∠ADB 的度数为
A. 40∘B. 50∘C. 60∘D. 20∘

6. 小明调查了班级里 20 位同学本学期购买课外书的花费情况，并将结果绘制成了下面的统计图．在这 20 位同学中，本学期购买课外书的花费的众数和中位数分别是
A. 50，50B. 50，30C. 80，50D. 30，50

7. 如图，正方形 ABCD 的边长为 4，点 E 在对角线 BD 上，且 ∠BAE=22.5∘，EF⊥AB，垂足为点 F，则 EF 的长为
A. 1B. 2C. 42−4D. 4−22

8. 如图，已知顶点为 −3,−6 的抛物线 y=ax2+bx+c 经过点 −1,−4，则下列结论中错误的是
A. b2>4ac
B. ax2+bx+c≥−6
C. 若点 −2,m，−5,n 在抛物线上，则 m>n
D. 关于 x 的一元二次方程 ax2+bx+c=−4 的两根为 x1=−5 和 x2=−1

二、填空题（共6小题；共30分）
9. 计算：27⋅83÷12= ．

10. “可燃冰”的开发成功，拉开了我国开发新能源的大门，目前发现我国南海“可燃冰”储存量达到 800 亿吨将 800 亿吨用科学记数法可表示为 吨．

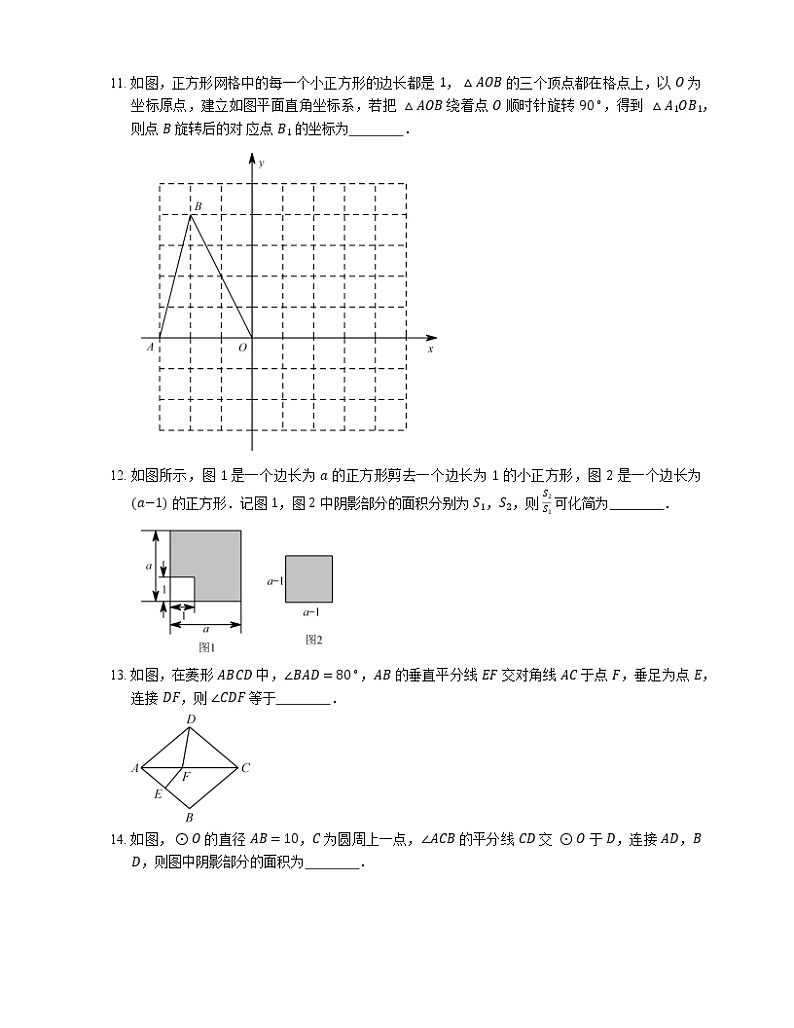
11. 如图，正方形网格中的每一个小正方形的边长都是 1，△AOB 的三个顶点都在格点上，以 O 为坐标原点，建立如图平面直角坐标系，若把 △AOB 绕着点 O 顺时针旋转 90∘，得到 △A1OB1，则点 B 旋转后的对 应点 B1 的坐标为 ．

12. 如图所示，图 1 是一个边长为 a 的正方形剪去一个边长为 1 的小正方形，图 2 是一个边长为 a−1 的正方形．记图 1，图 2 中阴影部分的面积分别为 S1，S2，则 S2S1 可化简为 ．

13. 如图，在菱形 ABCD 中，∠BAD=80∘，AB 的垂直平分线 EF 交对角线 AC 于点 F，垂足为点 E，连接 DF，则 ∠CDF 等于 ．

14. 如图，⊙O 的直径 AB=10，C 为圆周上一点，∠ACB 的平分线 CD 交 ⊙O 于 D，连接 AD，BD，则图中阴影部分的面积为 ．

三、解答题（共10小题；共130分）
15. 用圆规、直尺作图，不写作法，但要保留作图痕迹．
如图，A，B，C 为某公园的三个景点，景点 A 和景点 B 之间有一条笔直的小路，现要在小路上建一个凉亭 P，使景点 B 、景点 C 到凉亭 P 的距离之和等于景点 B 到景点 A 的距离，请用直尺和圆规在所给的图中作出点 P（不写作法和证明，只保留作图痕迹）．

16. （1）解方程：90x−6=60x．
（2）已知关于 x 的一元二次方程 12x2+13x−m=2 无实数根，求 m 的取值范围．

17. 为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图：
（1）求该班总人数；
（2）根据计算，请你补全两个统计图；
（3）已知该班甲同学四次训练成绩为 85，95，85，95，乙同学四次成绩分别为 85，90，95，90，现需从甲、乙两同学中选派一名同学参加校级比赛，你认为应该选派哪位同学并说明理由．

18. 小华和小军做摸卡片游戏，规则如下：甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标有的三个数值为 −7，−1，3．乙袋中的三张卡片所标的数值为 −2，1，6．先从甲袋中随机取出一张卡片，用 x 表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用 y 表示取出卡片上的数值，把 x，y 分别作为点 A 的横坐标和纵坐标．若点 A 在第一象限，则小华胜，若点 A 在第三象限则小军胜．这个游戏对双方公平吗?请说明理由．

19. 如图，李强在教学楼的点 P 处观察对面的办公大楼，为了求得对面办公大楼的高度，李强测得办公大楼顶部点 A 的仰角为 30∘，测得办公大楼底部点 B 的俯角为 37∘，已知测量点 P 到对面办公大楼上部 AD 的距离 PM 为 30 m，办公大楼平台 CD=10 m．求办公大楼的高度（结果保留整数）．（参考数据：sin37∘≈35，tan37∘≈34，3≈1.73）

20. 如图为某种材料温度 y∘C 随时间 xmin 变化的函数图象．已知该材料初始温度为 15∘C，温度上升阶段 y 与时间 x 成一次函数关系，且在第 5 分钟温度达到最大值 60∘C 后开始下降；温度下降阶段，温度 y 与时间 x 成反比例关系．
（1）分别求该材料温度上升和下降阶段，y 与 x 间的函数关系式；
（2）根据工艺要求，当材料的温度高于 30∘C 时，可以进行产品加工，问可加工多长时间?

21. 如图，在平行四边形 ABCD 中，点 O 是 AC 中点，AC=2AB，延长 AB 到 G，使 BG=AB，连接 GO 并延长，分别交 BC 于点 E，交 AD 于点 F．
（1）求证：△ABC≌△AOG；
（2）若 ABCD 为矩形，则四边形 AECF 是什么特殊四边形?请说明理由．

22. 如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分 ACB 和矩形的三边 AE，ED，DB 组成，已知河底 ED 是水平的，ED=16 m，AE=8 m，抛物线的顶点 C 到 ED 的距离是 11 m，以 ED 所在的直线为 x 轴，抛物线的对称轴为 y 轴建立平面直角坐标系．
（1）求抛物线的解析式；
（2）已知从某时刻开始的 40 小时内，水面与河底 ED 的距离 h（单位：m）随时间 t（单位：小时）的变化满足函数关系 h=−1128t−192+80≤t≤40 且当水面到顶点 C 的距离大于 5 m 时，允许船只通行，请通过计算说明：在这一时段内，有多少小时允许船只通行．

23. 问题提出：某段楼梯共有 10 个台阶，如果某同学在上台阶时，可以一步 1 个台阶，也可以一步 2 个台阶．那么该同学从该段楼梯底部上到顶部共有多少种不同的走法?
问题探究：为解决上述实际问题，我们先建立如下数学模型：
如图 ①，用若干个边长都为 1 的正方形（记为 1×1 矩形）和若干个边长分别为 1 和 2 的矩形（记为 1×2 矩形），要拼成一个如图 ② 中边长分别为 1 和 n 的矩形（记为 1×n 矩形），有多少种不同的拼法?（设 A1×n 表示不同拼法的个数）
为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化．
探究一：先从最特殊的情形入手，即要拼成一个 1×1 矩形，有多少种不同拼法?
显然，只有 1 种拼法，如图 ③，即 A1×1=1 种．
探究二：要拼成一个 1×2 矩形，有多少种不同拼法?
可以看出，有 2 种拼法，如图 ④，即 A1×2=2 种．
探究三：要拼成一个 1×3 矩形，有多少种不同拼法?
拼图方法可分为两类：一类是在图 ④ 这 2 种 1×2 矩形上方，各拼上一个 1×1 矩形，即这类拼法共有 A1×2=2 种；
另一类是在图 ③ 这 1 种 1×1 矩形上方拼上一个 1×2 矩形，即这类拼法有 A1×1=1 种．如图 ⑤，即 A1×3=A1×2+A1×1=2+1=3（种）．
（1）探究四：仿照上述探究过程，要拼成一个 1×4 矩形，有多少种不同拼法?请画示意图说明并求出结果．
（2）探究五：要拼成一个 1×5 矩形，仿照上述探究过程，得出 A1×5= 种不同拼法（直接写出结果，不需画图）．
（3）问题解决：请你根据上述中的数学模型，解答“问题提出”中的实际问题．（写出解答过程，不需画图）．

24. 如图，已知平行四边形 ABCD 中，AD=3 cm，CD=1 cm，∠B=45∘，点 P 从点 A 出发，沿 AD 方向匀速运动，速度为 3 cm/s；点 Q 从点 C 出发，沿 CD 方向匀速运动，速度为 1 cm/s，连接并延长 QP 交 BA 的延长线于点 M，过点 M 作 MN⊥BC，垂足是 N，设运动时间为 ts0（1）是否存在时刻 t，使点 P 在 ∠BCD 的平分线上；
（2）设四边形 ANPM 的面积为 Scm2，求 S 与 t 之间的函数关系式；
（3）是否存在某一时刻 t，使四边形 ANPM 与平行四边形 ABCD 面积相等，若存在，求出相应的 t 值，若不存在，说明理由；
（4）求 t 为何值时，△ABN 为等腰三角形．
答案
第一部分
1. A【解析】A．15 的倒数是 5，故A正确；
B．3 的相反数是 −3，故B错误；
C．4 的立方根是 4，故C错误；
D．2018 的绝对值是 2018，故D错误．
2. C【解析】第一个图形和第三个图形既是轴对称图形又是中心对称图形；
第二个图形是轴对称图形不是中心对称图形；
第四个图形不是轴对称图形，是中心对称图形．
3. B【解析】根据俯视图为三角形，主视图以及左视图都是矩形，可得这个几何体为三棱柱．
4. D【解析】解不等式 12x<1 得：x>−2，
解不等式 5−x≥0 得：x≤5，
∴ 不等式组的解集是 −25. B
【解析】∵AB 是 ⊙O 直径，AE 是 ⊙O 的切线，
∴∠BAD=90∘，
∵∠B=12∠AOC=40∘，
∴∠ADB=90∘−∠B=50∘．
6. A【解析】由扇形统计图可知，购买课外书花费为 100 元的同学有：20×10%=2（人），购买课外书花费为 80 元的同学有：20×25%=5（人），购买课外书花费为 50 元的同学有：20×40%=8（人），购买课外书花费为 30 元的同学有：20×20%=4（人），购买课外书花费为 20 元的同学有：20×5%=1（人），20 个数据为 100，100，80，80，80，80，80，50，50，50，50，50，50，50，50，30，30，30，30，20，在这 20 位同学中，本学期计划购买课外书的花费的众数为 50，中位数为 50+50÷2=50．
7. D【解析】如图，在 AF 上取 FG=EF，连接 GE．
∵EF⊥AB，
∴△EFG 是等腰直角三角形，
∴EG=2EF，∠EGF=45∘，
由三角形的外角性质得：∠BAE+∠AEG=∠EGF．
∵∠BAE=22.5∘，∠EGF=45∘，
∴∠BAE=∠AEG=22.5∘，
∴AG=EG，
在正方形 ABCD 中，∠ABD=45∘，
∴△BEF 是等腰直角三角形，
∴BF=EF，
设 EF=x．
∵AB=AG+FG+BF，
∴4=2x+x+x，
解得：x=22−2=4−22．
8. C【解析】A．图象与 x 轴有两个交点，方程 ax2+bx+c=0 有两个不相等的实数根，b2−4ac>0，所以 b2>4ac，故A选项正确；
B．抛物线的开口向上，函数有最小值，最小值为 −6，所以 ax2+bx+c≥−6，故B选项正确；
C．抛物线的对称轴为直线 x=−3，因为 x 轴上 −5 离对称轴的距离大于 −2 离对称轴的距离，所以 mD．根据抛物线的对称性可知，−1,−4 关于对称轴的对称点为 −5,−4，所以关于 x 的一元二次方程 ax2+bx+c=−4 的两根为 x1=−5 和 x2=−1，故D选项正确．
第二部分
9. 12
【解析】27⋅83÷12=33×83÷12=33×83×2=12.
10. 8×1010
【解析】800亿=8×1010．
11. 4,2
12. a−1a+1
【解析】S1S2=a2−1a−12=a−1a+1a−12=a+1a−1，
所以 S2S1=a−1a+1．
13. 60∘
【解析】连接 BF，
∵ 四边形 ABCD 是菱形，
∴△ABC 和 △ADC 关于 AC 对称，AB∥CD，∠BAC=∠DAC=40∘，
∴∠ADF=∠ABF，∠ADC+∠BAD=180∘，
∵EF 是 AB 的垂直平分线，∠BAD=80∘，
∴AF=BF，∠ADC=100∘，
∴∠ABF=∠BAC=40∘，
∴∠ADF=40∘，
∴∠CDF=100∘−40∘=60∘．
14. 252+254π
【解析】如图，连接 OD．
∵AB 是直径，且 AB=10，
∴∠ACB=90∘，AO=BO=DO=5．
∵CD 平分 ∠ACB，
∴∠ABD=∠ACD=12∠ACB=45∘，
∴∠AOD=90∘，
则阴影部分的面积是 S扇形AOD+S△BOD=90⋅π⋅52360+12×5×5=252+25π4．
第三部分
15. 如图，连接 AC，作线段 AC 的垂直平分线 MN，直线 MN 交 AB 于 P．
点 P 即为所求的点．
理由：
∵MN 垂直平分线段 AC，
∴PA=PC，
∴PC+PB=PA+PB=AB．
16. （1） 方程两边乘以 xx−6 得：90x=60x−6，
解得：x=−12．
经检验：x=−12 是原方程的根．
∴ 分式方程的根为 x=−12．
（2） ∵ 关于 x 的一元二次方程 12x2+13x−m=2 没有实数根，
∴△=132−4×12×−m−2<0，解得：m<−3718，
∴m 的值取值范围为 m<−3718．
17. （1） 由题意可得：该班总人数是：22÷55%=40（人）；
（2） 由（1）得：第四次优秀的人数为：40×85%=34（人），第三次优秀率为：3240×100%=80%；
如图所示：
（3） 答案不唯一．
如：选乙，理由甲乙平均分相同都是 90 分，但 S甲2=25>S乙2=252，乙成绩稳．
（选甲，理由甲乙平均分相同都是 90 分，但甲的众数是 85，95，更易冲击高分）回答合理即可．
18. 列表如下：
−7−13−2−7,−2−1,−23,−21−7,1−1,13,16−7,6−1,63,6
点 Ax,y 共 9 种等可能的情况，
∴P小华胜=29，P小军胜=29，
∴ 游戏公平．
19. 过点 C 向 PM 作垂线 CN，垂足为 N．
在 △PMA 中，
∵∠APM=30∘，
∴PM=3AM=30，解得：AM=103≈17.3．
∵ 四边形 NCDM 是长方形，
∴CD=NM，NC=MD，
∴PN=PM−NM=PM−CD=20，
在 Rt△PBN 中，
∵tan37∘=BNPN≈34，
∴BN≈34×20=15，
∴ 总高度 h=AM+BN=32.3≈32m．
答：办公大楼的高度约为 32 m．
20. （1） 设温度上升阶段一次函数表达式为 y=kx+bk≠0．
∵ 该函数图象经过点 0,15，5,60，
∴b=15,5k+b=60, 解得：k=9,b=15.
∴ 一次函数的表达式为 y=9x+150≤x≤5．
设温度下降阶段反比例函数表达式为 y=axa≠0．
∵ 该函数图象经过点 5,60，
∴a5=60，解得：a=300．
∴ 反比例函数表达式为 y=300xx≥5．
（2） ∵y=9x+15，
∴ 当 y=30 时，9x+15=30，解得：x=53．
∵y=300x，
∴ 当 y=30 时，300x=30，解得：x=10，10−53=253．
∴ 可加工的时间为 253 分钟．
21. （1） ∵O 是 AC 的中点，AC=2AB，BG=AB，
∴AO=AB，AC=AG．
在 △ABC 和 △AOG 中，
AB=AO,∠BAC=∠OAG,AC=AG.
∴△ABC≌△AOGSAS．
（2） 四边形 AECF 是菱形．理由如下：
∵O 是 AC 的中点，
∴AO=OC．
∵ 四边形 ABCD 是平行四边形，
∴AF∥EC，
∴∠DAO=∠BCO．
在 △AOF 和 △COE 中，
∠AOF=∠COE,∠FAO=∠ECO,AO=CO.
∴△AOF≌△COE．
∴AF=CE，
∴ 四边形 AECF 是平行四边形．
由（1）知 △ABC≌△AOG，
∴∠AOG=∠ABC．
∵ 四边形 ABCD 是矩形，
∴∠ABC=90∘，
∴∠AOG=90∘，
∴ 平行四边形 AECF 是菱形．
22. （1） ∵ 点 C 到 ED 的距离是 11 米，
∴OC=11，
设抛物线的解析式为 y=ax2+11，
由题意得 B8,8，
代入解析式中得 64a+11=8，
解得 a=−364，
∴y=−364x2+11．
（2） 水面到顶点 c 的距离大于 5 米时，即水面与河底 ED 的距离 h 至多为 11−5=6（米），
∴6=−1128t−192+8，
∴t−192=256，
∴t−19=±16，
解得 t1=35，t2=3，
∴40−35−3=8（小时）．
答：有 8 小时允许船只通过．
23. （1） 拼图方法可分为两类：一类是在图 ④ 这 2 种 1×2 矩形上方，各拼上一个 1×2 矩形，即这类拼法共有 A1×2=2 种；另一类是在图 ⑤ 这 3 种 1×3 矩形上方，各拼上一个 1×1 矩形，即这类拼法共有 A1×3=3 种．如图，
即 A1×4=A1×3+A1×2=3+2=5（种）．
（2） 8
【解析】∵A1×4=A1×2+A1×3=5，A1×5=A1×3+A1×4=3+5=8，
∴ 要拼成一个 1×5 矩形，有 8 种不同拼法 A1×5．
（3） ∵ 楼梯共有 10 个台阶，如果某同学在上台阶时，可以一步 1 个台阶，也可以一步 2 个台阶，
∴A1×1=1（种），即 A1×3=A1×2+A1×1=2+1=3（种），A1×4=A1×3+A1×2=3+2=5（种），A1×5=8（种），
∴A1×6=A1×4+A1×5=5+8=13（种），A1×7=A1×6+A1×5=13+8=21（种），
∴A1×8=A1×6+A1×7=13+21=34（种），
∴A1×9=A1×7+A1×8=21+34=55（种），
∴A1×10=A1×8+A1×9=34+55=89（种）．
答：该同学从该段楼梯底部上到顶部共有 89 种不同的走法．
24. （1） 如图 1，连接 PC．
当 PC 平分 ∠BCD 时，则 ∠DCP=∠PCB，
∵AD∥BC，
∴∠DPC=∠PCB，
∴∠DPC=∠DCP，
∴DC=PD．
∵DC=1，PD=3−3t，
∴3−3t=1，3t=2，t=23．
（2） ∵ 四边形 ABCD 是平行四边形，
∴AB∥CD，
∴∠MAP=∠QDP．
又 ∵∠MPA=∠QPD，
∴△MAP∽△QDP．
∴AMDQ=PAPD，
∴AM1−t=3t3−3t，
解得：AM=t．
∵AB=CD=1，
∴MB=1+t．
∵MN⊥BC，∠B=45∘，
∴sin45∘=MNMB=MN1+t=22，
∴MN=221+t．
又 ∵ 四边形 ABCD 是平行四边形，
∴AD∥BC，
又 ∵MN⊥BC，
∴MN⊥AD，
∴S四边形ANPM=S△MAP+S△NAP=12AP⋅OM+12AP⋅ON=12AP⋅OM+ON=12AP⋅MN=12⋅3t⋅221+t=324t2+324t.
∴S 与 t 之间的函数关系式为 S=324t2+324t0 （3） 不存在．理由如下：
如图 2，过点 A 作 AG⊥BC 于点 G．
∵∠B=45∘，AB=1，
∴AG=22．
∵S四边形ANPM=S平行四边形ABCD，
∴324t2+324t=3×22，
∴t2+t−2=0，
解得：t=−2，t=1．
∵0 ∴ 不存在在某一时刻 t，使四边形 ANPM 与平行四边形 ABCD 面积相等．
（4） 由（2）可知：AM=t，
∴BM=1+t．
∵∠B=45∘，
∴MN=BN=22t+1，AD∥BC．
∴∠MAD=∠B=45∘，∠AOM=∠BNM=90∘．
∵AM=t，
∴AO=MO=22t，
∵NO=AG=22，
∴AN=12t2+12．分三种情况讨论：
① 当 AB=BN 时，22t+1=1，解得：t=2−1；
② 当 AB=AN 时，12t2+12=1，解得：t=1（舍去）；
③ 当 BN=AN 时，22t+1=12t2+12 时，解得：t=0（舍）．
综上所述：当 t=2−1 时，△ABN 为等腰三角形．