2019年云南省昆明市盘龙区、禄劝县中考二模数学试卷

这是一份2019年云南省昆明市盘龙区、禄劝县中考二模数学试卷，共14页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。
一、填空题（共6小题；共30分）
1. −1 的相反数是 ．

2. 分解因式：x3−2x2+x= ．

3. 通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题．如果从某个多边形的一个顶点出发的对角线共有 2 条，那么该多边形的内角和是 度．

4. 如图，四边形 ABCD 内接于 ⊙O，∠BCD=120∘，则 ∠BOD= 度．

5. 若关于 x 的一元二次方程 kx2−2x−1=0 有两个不相等的实数根，则实数 k 的取值范围是 ．

6. 矩形 ABCD 中，AB=6，BC=8．点 P 在矩形 ABCD 的内部，点 E 在边 BC 上，满足 △PBE∽△DBC，若 △APD 是等腰三角形，则 PE 的长为 ．

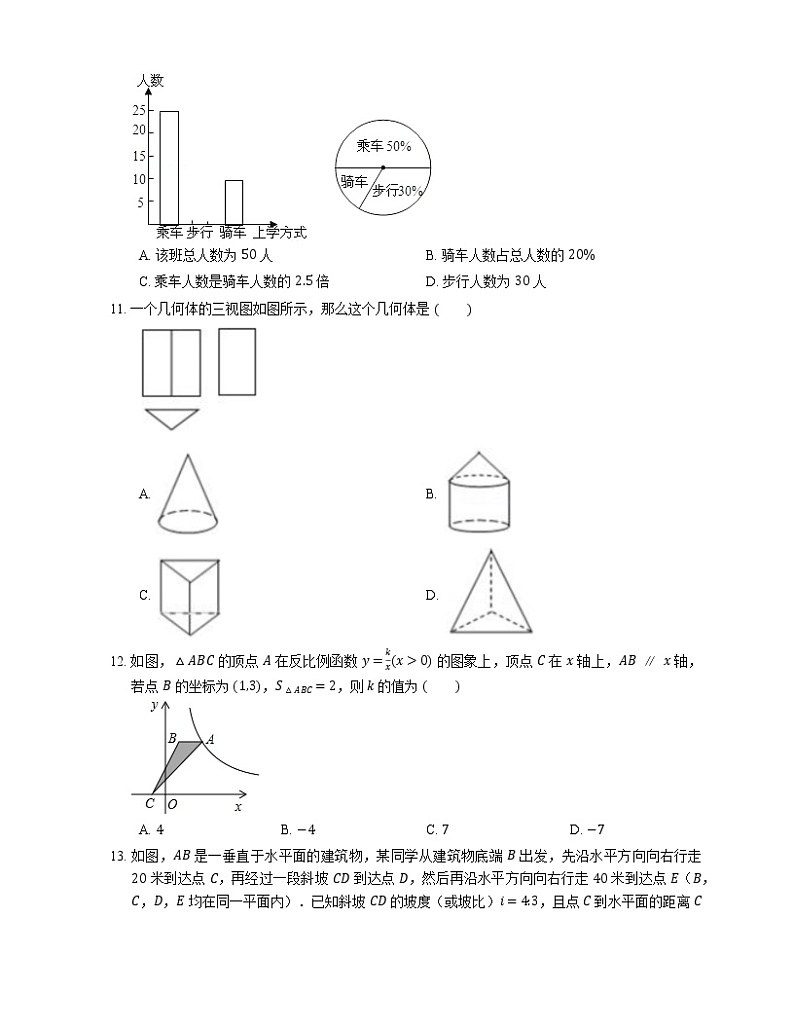
二、选择题（共8小题；共40分）
7. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为 0.056 盎司．将 0.056 用科学记数法表示为
A. 5.6×10−1B. 5.6×10−2C. 5.6×10−3D. 0.56×10−1

8. 函数 y=11−x 的自变量 x 的取值范围是
A. x>1B. x≠1C. x0 的图象上，顶点 C 在 x 轴上，AB∥x 轴，若点 B 的坐标为 1,3，S△ABC=2，则 k 的值为
A. 4B. −4C. 7D. −7

13. 如图，AB 是一垂直于水平面的建筑物，某同学从建筑物底端 B 出发，先沿水平方向向右行走 20 米到达点 C，再经过一段斜坡 CD 到达点 D，然后再沿水平方向向右行走 40 米到达点 E（B，C，D，E 均在同一平面内）．已知斜坡 CD 的坡度（或坡比）i=4:3，且点 C 到水平面的距离 CF 为 8 米，在 E 处测得建筑物顶端 A 的仰角为 24∘，则建筑物 AB 的高度约为 （参考数据：sin24∘=0.41，cs24∘=0.91，tan24∘=0.45）
A. 21.7 米B. 224 米C. 274 米D. 28.8 米

14. 如图，△ABC 中，∠ACB=90∘，AB=10，tanA=12．点 P 是斜边 AB 上一个动点．过点 P 作 PQ⊥AB，垂足为 P，交边 AC（或边 CB）于点 Q，设 AP=x，△APQ 的面积为 y，则 y 与 x 之间的函数图象大致为
A. B.
C. D.

三、解答题（共9小题；共117分）
15. 计算：3−8+π−20190−4cs30∘+−12．

16. 设 M=1a2−1÷1+1a−1．
（1）化简 M；
（2）当 a=1 时，记此时 M 的值为 f1=11×2=1−12；
当 a=2 时，记此时 M 的值为 f2=12×3=12−13；
当 a=3 时，记此时 M 的值为 f3=13×4=13−14；
⋯⋯
当 a=n 时，记此时 M 的值为 fn= ；
则 f1+f2+⋯+fn= ．
（3）解关于 x 的不等式组：x−22−2−x4≤f1+f2+f3,−x0，即 −22−4×k×−1>0，解得 k>−1 且 k≠0．
∴k 的取值范围为 k>−1 且 k≠0．
6. 65 或 3
【解析】∵ 四边形 ABCD 为矩形，
∴∠BAD=90∘，
∴BD=AB2+AD2=10，
当 PD=DA=8 时，BP=BD−PD=2，
∵△PBE∽△DBC，
∴BPBD=PECD，即 210=PE6，
解得，PE=65，
当 PʹD=PʹA 时，点 Pʹ 为 BD 的中点，
∴PʹEʹ=12CD=3．
第二部分
7. B
8. C【解析】由题意得 1−x>0，解得 x0 的图象上，
∴k=7．
13. A【解析】作 BM⊥ED 交 ED 的延长线于 M，
∵CF⊥DE，
在 Rt△CDF 中，
∵CFDF=43，CF=8，
∴DF=6，
∴CD=10，
∴CF=8，
∵ 四边形 BMNC 是矩形，
∴BM=CF=8，BC=MF=20，EM=MF+DF+DE=66，
在 Rt△AEM 中，tan24∘=AMEM，
∴0.45=8+AB66，
∴AB=21.7（米）．
14. B【解析】设 BC=a，则 AC=2a（a>0），
∴ 在 Rt△ACB 中，AB=AC2+BC2，
∴ a=25，BC=25，AC=45，
当 0≤x≤8 时，易证 △APQ∽△ACB，
∴ APAC=QPBC=x45，
∴ y=S△APQ=12AP×PQ=14x2，
当 8