

2018年广东省佛山市南海区里水镇中考二模数学试卷
展开一、选择题(共10小题;共50分)
1. −2008 的相反数是
A. 2008B. −2008C. 12008D. −12008
2. 如图是由 4 个大小相同的正方体组合而成的几何体,其俯视图是
A. B.
C. D.
3. PM2.5 是指大气中直径不大于 0.0000025 米的颗粒物,将 0.0000025 用科学记数法表示为
A. 2.5×105B. 2.5×106C. 2.5×10−5D. 2.5×10−6
4. 下面的计算正确的是
A. 3x2⋅4x2=12x2B. x3⋅x5=x15C. x4÷x=x3D. x52=x7
5. 下列所述的图形中,既是轴对称图形,又是中心对称图形的是
A. 平行四边形B. 等腰直角三角形
C. 菱形D. 正五边形
6. 不等式组 2−x>1,5x>3x−2 的解集是
A. x>1B. −3
7. 如图,已知 DE∥BC,AB=AC,∠1=125∘,则 ∠C 的度数是
A. 55∘B. 45∘C. 35∘D. 65∘
8. 某校“环保小组”的 5 名同学在一次活动中捡废弃塑料袋的个数分别是:4,6,8,6,10,这组数据的中位数,众数分别为
A. 8,6B. 6,8C. 6,6D. 8,10
9. 关于 x 的一元二次方程 x2+2x−m=0 有实数根,则 m 的取值范围是
A. m≥−1B. m>−1C. m≤−1D. m<−1
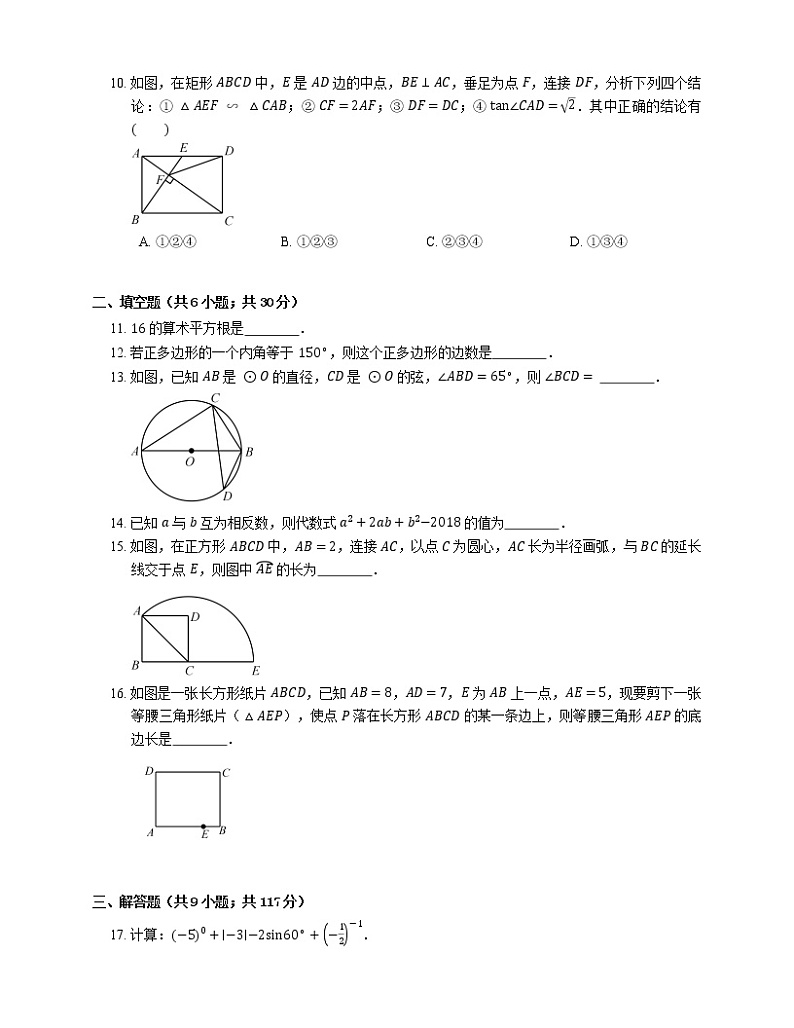
10. 如图,在矩形 ABCD 中,E 是 AD 边的中点,BE⊥AC,垂足为点 F,连接 DF,分析下列四个结论:① △AEF∽△CAB;② CF=2AF;③ DF=DC;④ tan∠CAD=2.其中正确的结论有
A. ①②④B. ①②③C. ②③④D. ①③④
二、填空题(共6小题;共30分)
11. 16 的算术平方根是 .
12. 若正多边形的一个内角等于 150∘,则这个正多边形的边数是 .
13. 如图,已知 AB 是 ⊙O 的直径,CD 是 ⊙O 的弦,∠ABD=65∘,则 ∠BCD= .
14. 已知 a 与 b 互为相反数,则代数式 a2+2ab+b2−2018 的值为 .
15. 如图,在正方形 ABCD 中,AB=2,连接 AC,以点 C 为圆心,AC 长为半径画弧,与 BC 的延长线交于点 E,则图中 AE 的长为 .
16. 如图是一张长方形纸片 ABCD,已知 AB=8,AD=7,E 为 AB 上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点 P 落在长方形 ABCD 的某一条边上,则等腰三角形 AEP 的底边长是 .
三、解答题(共9小题;共117分)
17. 计算:−50+∣−3∣−2sin60∘+−12−1.
18. 先化简,再求值:2x−2x÷x−1x,其中 x=−3.
19. 在咸宁创建“国家卫生城市”的活动中,市园林公司加大了对市区主干道两旁植“景观树”的力度,平均每天比原计划多植 5 棵,现在植 60 棵所需的时间与原计划植 45 棵所需的时间相同,问现在平均每天植多少棵树?
20. 如图所示,在 △ABC 中,AB=AC,∠A=36∘.
(1)作 ∠ABC 的平分线 BD,交 AC 于点 D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,比较线段 DA 与 BC 的大小关系,请说明理由.
21. 如图,将矩形 ABCD 沿对角线 BD 对折,点 C 落在 E 处,BE 与 AD 相交于点 F.
(1)求证:△BFD 是等腰三角形;
(2)若 BC=4,CD=2,求 ∠AFB 的余弦值.
22. 据某网站调查,2016 年全国网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如图:
根据以上信息解答下列问题:
(1)请补全条形统计图;
(2)如果某市约有 300 万人口,请你估计该市最关注教育问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,请用列表法或树形图法表示抽取的两人恰好是甲和乙的概率.
23. 如图,已知直线 l:y=ax+b 与反比例函数 y=−4x 的图象交于 A−4,1,Bm,−4,且直线 l 与 y 轴交于点 C.
(1)求直线 l 的解析式;
(2)若不等式 ax+b>−4x 成立,则 x 的取值范围是 ;
(3)若直线 x=nn<0 与 y 轴平行,且与双曲线交于点 D,与直线 l 交于点 H,连接 OD,OH,OA,当 △ODH 的面积是 △OAC 面积的一半时,求 n 的值.
24. 如图,AB 是 ⊙O 的直径,D,E 为 ⊙O 上位于 AB 异侧的两点,连接 BD 并延长至点 C,使得 CD=BD,连接 AC 交 ⊙O 于点 F,连接 AE,DE,DF.
(1)证明:∠E=∠C;
(2)若 ∠E=55∘,求 ∠BDF 的度数;
(3)设 DE 交 AB 于点 G,若 DF=4,csB=23,E 是 AB 的中点,求 EG⋅ED 的值.
25. 如图 1,在 △ABC 中,AB=AC=4,∠ABC=67.5∘,△ABD 和 △ABC 关于 AB 所在的直线对称,点 M 为边 AC 上的一个动点(重合),点 M 关于 AB 所在直线的对称点为 N,△CMN 的面积为 S.
(1)求 ∠CAD 的度数;
(2)设 CM=x,求 S 与 x 的函数表达式,并求 x 为何值时 S 的值最大?
(3)S 的值最大时,过点 C 作 EC⊥AC 交 AB 的延长线于点 E,连接 EN(如图 2),P 为线段 EN 上一点,Q 为平面内一点,当以 M,N,P,Q 为顶点的四边形是菱形时,请直接写出所有满足条件 NP 的长.
答案
第一部分
1. A
2. B
3. D
4. C
5. C
【解析】A.平行四边形不是轴对称图形,是中心对称图形,故本选项错误;
B.等腰直角三角形是轴对称图形,不是中心对称图形,故本选项错误;
C.菱形既是轴对称图形,又是中心对称图形,故本选项正确;
D.正五边形是轴对称图形,不是中心对称图形,故本选项错误.
6. B【解析】2−x>1, ⋯⋯①5x>3x−2, ⋯⋯②
∵ 解不等式 ① 得:x<1;解不等式 ② 得:x>−3,
∴ 不等式组的解集为 −3
∴∠ADE=180∘−125∘=55∘,
∵DE∥BC,AB=AC,
∴AD=AE,∠C=∠AED,
∴∠AED=∠ADE=55∘,
∴∠C=55∘.
8. C【解析】把这组数据从小到大排列为 4,6,6,8,10,最中间的数是 6,则中位数是 6;
6 出现了 2 次,出现的次数最多,则众数是 6.
9. A【解析】∵ 关于 x 的一元二次方程 x2+2x−m=0 有实数根,
∴Δ=22−4×1×−m=4+4m≥0,
解得:m≥−1.
10. B
【解析】如图,过 D 作 DM∥BE 交 AC 于 N,
∵ 四边形 ABCD 是矩形,
∴AD∥BC,∠ABC=90∘,AD=BC,
∵BE⊥AC 于点 F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90∘,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴AEBC=AFCF,
∵AE=12AD=12BC,
∴AFCF=12,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴ 四边形 BMDE 是平行四边形,
∴BM=DE=12BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC 于点 F,DM∥BE,
∴DN⊥CF,
∴DM 垂直平分 CF,
∴DF=DC,故③正确;
设 AE=a,AB=b,则 AD=2a,
由 △BAE∽△ADC,有 ba=2ab,即 b=2a,
∴tan∠CAD=DCAD=b2a=22,故④不正确;
正确的有①②③.
第二部分
11. 4
12. 12
【解析】∵ 正多边形的一个内角等于 150∘,
∴ 它的外角是:180∘−150∘=30∘,
∴ 它的边数是:360∘÷30∘=12.
13. 25∘
【解析】∵AB 是直径,
∴∠ACB=90∘,
∵∠ACD=∠ABD=65∘,
∴∠BCD=90∘−65∘=25∘.
14. −2018
【解析】∵a 与 b 互为相反数,
∴a+b=0,则
原式=a2+2ab+b2−2018=a+b2−2018=0−2018=−2018.
15. 322π
【解析】∵ 四边形 ABCD 为正方形,
∴CA=2AB=22,∠ACB=45∘,
∴∠ACE=135∘,
∴AE的长度=135⋅π⋅22180=322π.
16. 52 或 45 或 5
第三部分
17. 原式=1+3−2×32+−2=1+3−3−2=2−3.
18. 当 x=−3 时,
原式=2x−1x⋅xx+1x−1=2x+1=−1.
19. 设现在平均每天植 x 棵树,则原计划平均每天植树 x−5,依题意得 60x=45x−5,解得
x=20,
经检验 x=20 是原方程的解,且符合题意.
答:现在平均每天植 20 棵树.
20. (1) 如图所示,BD 为所作;
(2) 线段 DA=BC.理由如下:
∵AB=AC,
∴∠ABC=∠C=12180∘−36∘=72∘,
∵BD 平分 ∠ABC,
∴∠ABD=∠CBD=36∘,
∴∠ABD=∠A,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72∘,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BC.
21. (1) 依题意,∠1=∠2,
∵ 四边形 ABCD 是矩形,
∴AD∥BC,
∴∠2=∠3,
∴∠1=∠3,
∴△BFD 为等腰三角形.
(2) 由(1)可知 BF=DF,设 BF=x,则 AF=4−x,
在 Rt△BAF 中,4−x2+22=x2,解得:x=52,
∴AF=4−52=32,
∴cs∠AFB=35.
22. (1) ∵ 调查的总人数是:140÷10%=1400(人),
∴ 关注教育的人数是:1400×25%=350(人),
补全图形如图:
(2) 300×25%=75 万人,
∴ 估计最关注环保问题的人数约为 75 万人.
(3) 画树形图得:
则 P抽取的两人恰好是甲和乙=212=16.
23. (1) ∵y=−4x,Bm,−4,
∴m=1,
∴B1,−4.
∵y=ax+b 过 A−4,1,B1,−4,
∴−4a+b=1,a+b=−4,
解得 a=−1,b=−3,
∴ 直线解析式为 y=−x−3.
(2) x<−4 或 0
∴S△OAC=12×3×4=6.
由直线 x=n 可知 Dn.−4n,Hn,−n−3,
当 −4
∴12DH⋅−n=3 即 12−4n+n+3⋅−n=3,
整理得 n2+3n+2=0,
解得:n1=−1,n2=−2;
当 n<−4 时,DH=−n−3−−4n=−n−3+4n,
∵S△ODH=12S△OAC=12×6=3,
∴12DH⋅−n=3 即 12−n−3+4n⋅−n=3,
整理得 n2+3n−10=0,
解得:n1=−5,n2=2(不合题意,舍去).
综上可知 n 的值为 −1,−2,−5.
24. (1) 连接 AD,
∵AB 是 ⊙O 的直径,
∴∠ADB=90∘,即 AD⊥BC,
∵CD=BD,
∴AD 垂直平分 BC,
∴AB=AC,
∴∠B=∠C,
又 ∵∠B=∠E,
∴∠E=∠C.
(2) ∵ 四边形 AEDF 是 ⊙O 的内接四边形,
∴∠AFD=180∘−∠E,
又 ∵∠CFD=180∘−∠AFD,
∴∠CFD=∠E=55∘,
又 ∵∠E=∠C=55∘,
∴∠BDF=∠C+∠CFD=110∘.
(3) 连接 OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在 Rt△ABD 中,csB=23,BD=4,
∴AB=6,
∵E 是 AB 的中点,AB 是 ⊙O 的直径,
∴∠AOE=90∘,
∵AO=OE=3,
∴AE=33,
∵E 是 AB 的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴AEEG=DEAE,即 EG⋅ED=AE2=18.
25. (1) ∵AB=AC,∠ABC=67.5∘,
∴∠ACB=∠ABC=67.5∘,
∴∠CAB=180∘−67.5∘−67.5∘=45∘,
∵△ABD 和 △ABC 关于 AB 所在的直线对称,
∴∠DAB=∠CAB=45∘,
∴∠CAD=45∘+45∘=90∘.
(2) 由(1)知:AN⊥AM,
∵ 点 M,N 关于 AB 所在直线对称,
∴AM=AN,
∵CM=x,
∴AN=AM=4−x,
∴S=12×CM×AN=12x4−x,
∴S=−12x2+2x,
∴ 当 x=−22×−12=2 时,S 有最大值.
(3) 所有满足条件 NP 的长是 25 或 22 或 455.
【解析】∵CE⊥AC,
∴∠ECA=90∘,
∵∠CAB=45∘,
∴∠CEA=∠EAC=45∘,
∴CE=AC=4,
在 Rt△ECA 中,AC=EC=4,由勾股定理得:EA=42+42=42,
∵AM=AN,∠CAB=∠DAB,
∴AO⊥MN,MO=NO,
在 Rt△MAN 中,AM=AN=4−2=2,由勾股定理得:MN=22+22=22,
∴MO=NO=2,
由勾股定理得:AO=22−22=2,
∴EO=42−2=32,
在 Rt△EON 中,EO=32,MO=2,由勾股定理得:EM=322+22=25,
分为三种情况:
①当以 MN 为对角线时,此时 P 在 E 上,即 NP=NE=25;
②以 MN 为一边时,以 N 为圆心,以 MN 为半径画弧交 NE 于 P,
此时 NP=MN=22;
③以 MN 为一边时,过 M 作 MZ⊥NE 于 Z,
则 PZ=NZ,
∵AE⊥MN,
∴∠EON=∠MZN=90∘,
∵∠ENO=∠MNZ,
∴△ENO∽△MNZ,
∴ENMN=NOZN,
∴2522=2ZN,
∴ZN=255,
∴NP=2ZN=455,
即所有满足条件 NP 的长是 25 或 22 或 455.
广东省佛山市南海区里水镇2023-2024学年数学九上期末质量检测模拟试题含答案: 这是一份广东省佛山市南海区里水镇2023-2024学年数学九上期末质量检测模拟试题含答案,共9页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
2023-2024学年广东省佛山市南海区里水镇数学九上期末学业水平测试试题含答案: 这是一份2023-2024学年广东省佛山市南海区里水镇数学九上期末学业水平测试试题含答案,共7页。试卷主要包含了下列函数是二次函数的是,已知点A等内容,欢迎下载使用。
广东省佛山市南海区里水镇2023-2024学年八上数学期末监测模拟试题含答案: 这是一份广东省佛山市南海区里水镇2023-2024学年八上数学期末监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列运算结果正确的是等内容,欢迎下载使用。












