2018年北京市大兴区中考一模数学试卷

这是一份2018年北京市大兴区中考一模数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 若 a=10，则实数 a 在数轴上对应的点的大致位置是
A. 点 EB. 点 FC. 点 GD. 点 H

2. 下列运算正确的是
A. 2a23=6a6B. a3⋅a2=a5
C. 2a2+4a2=6a4D. a+2b2=a2+4b2

3. 已知一个多边形的内角和是它的外角和的 2 倍，那么这个多边形的边数是
A. 3B. 4C. 5D. 6

4. 如图，AD∥BC，点 E 在 BD 的延长线上，若 ∠ADE=150∘，则 ∠DBC 的度数为
A. 30∘B. 50∘C. 60∘D. 150∘

5. 如图，⊙O 的直径 AB 垂直于弦 CD，垂足是 E，∠A=22.5∘，OC=6，则 CD 的长为
A. 3B. 32C. 6D. 62

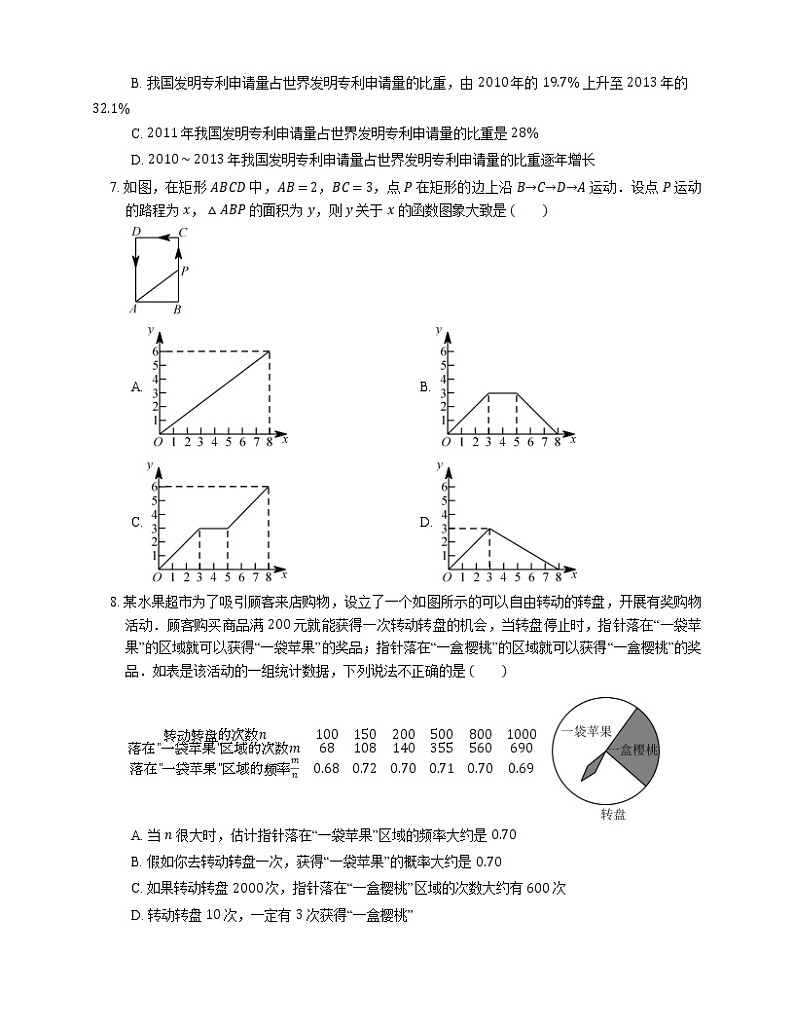
6. 自 2008 年实施国家知识产权战略以来，我国具有独立知识产权的发明专利日益增多．如图显示了 2010∼2013 年我国发明专利申请量占世界发明专利申请量的比重．根据统计图提供的信息，下列说法不合理的是
A. 统计图显示了 2010∼2013 年我国发明专利申请量占世界发明专利申请量的比重的情况
B. 我国发明专利申请量占世界发明专利申请量的比重，由 2010 年的 19.7% 上升至 2013 年的 32.1%
C. 2011 年我国发明专利申请量占世界发明专利申请量的比重是 28%
D. 2010∼2013 年我国发明专利申请量占世界发明专利申请量的比重逐年增长

7. 如图，在矩形 ABCD 中，AB=2，BC=3，点 P 在矩形的边上沿 B→C→D→A 运动．设点 P 运动的路程为 x，△ABP 的面积为 y，则 y 关于 x 的函数图象大致是
A. B.
C. D.

8. 某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动．顾客购买商品满 200 元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品；指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品．如表是该活动的一组统计数据，下列说法不正确的是
转动转盘的次数n1001502005008001000落在"一袋苹果"区域的次数m68108140355560690落在"一袋苹果"区域的频率
A. 当 n 很大时，估计指针落在“一袋苹果”区域的频率大约是 0.70
B. 假如你去转动转盘一次，获得“一袋苹果”的概率大约是 0.70
C. 如果转动转盘 2000 次，指针落在“一盒樱桃”区域的次数大约有 600 次
D. 转动转盘 10 次，一定有 3 次获得“一盒樱桃”

二、填空题（共8小题；共40分）
9. 计算：18−−370−12−1−−2= ．

10. 分解因式：a3−ab2= ．

11. 请写出一个开口向下，并且对称轴为直线 x=1 的抛物线的表达式 y= ．

12. 如图 1，将边长为 a 的大正方形剪去一个边长为 b 的小正方形，并沿图中的虚线剪开，拼接后得到图 2，根据图形的面积写出一个含字母 a,b 的等式： ．

13. 在读书活动中，某同学对甲、乙两个班学生的读书情况进行了统计：甲班学生人数比乙班学生人数多 3 人，甲班学生读书 480 本，乙班学生读书 360 本，乙班平均每人读书的本数是甲班平均每人读书的本数的 45．求甲、乙两班各有多少人?设乙班有 x 人，则甲班有 x+3 人，依题意，可列方程为 ．

14. 若 xy=32，则 5y2x−2y−x−2y÷x2−6xy+9y2x−2y 的值是 ．

15. 如图，在 Rt△ABC 中，∠C=90∘，AC=BC，将 Rt△ABC 绕点 A 逆时针旋转 15∘ 得到 Rt△ABʹCʹ，BʹCʹ 交 AB 于 E，若图中阴影部分面积为 23，则 BʹE 的长为 ．

16. 下面是“求作 ∠AOB 的角平分线”的尺规作图过程．
已知：如图，钝角 ∠AOB．
求作：∠AOB 的角平分线．
作法：
①在 OA 和 OB 上，分别截取 OD，OE，使 OD=OE；
②分别以 D，E 为圆心，大于 12DE 的长为半径作弧，在 ∠AOB 内，两弧交于点 C；
③作射线 OC．
所以射线 OC 就是所求作的 ∠AOB 的角平分线．
请回答：该尺规作图的依据是 ．

三、解答题（共12小题；共156分）
17. 解不等式组 2x+3≤4x+7,x+22>x. 并写出它的所有整数解．

18. 我国汉代数学家赵爽为了证明勾股定理，创造了一幅“弦图”后人称其为“赵爽弦图”（如图 1）．图 2 是弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形 ABCD，正方形 EFGH，正方形 MNKT 的面积分别为 S1，S2，S3，若 S1+S2+S3=10，求 S2 的值．
以下是求 S2 的值的解题过程，请你根据图形补充完整．
解：设每个直角三角形的面积为 S，
S1−S2= （用含 S 的代数式表示）， ⋯⋯①
S2−S3= （用含 S 的代数式表示）， ⋯⋯②
由 ①，② 得，S1+S3= ．
∵S1+S2+S3=10，
∴2S2+S2=10．
∴S3=103．

19. 如图，在 △ABC 中，AB=AC，点 D，点 E 分别是 BC，AC 上一点，且 DE⊥AD．若 ∠BAD=55∘，∠B=50∘，求 ∠DEC 的度数．

20. 已知关于 x 的一元二次方程 3x2−6x+1−k=0 有实数根，k 为负整数．
（1）求 k 的值；
（2）如果这个方程有两个整数根，求出它的根．

21. 如图，矩形 ABCD 的对角线 AC 、 BD 交于点 O，且 DE∥AC，CE∥BD．
（1）求证：四边形 OCED 是菱形；
（2）若 ∠BAC=30∘，AC=4，求菱形 OCED 的面积．

22. 如图，点 A 是直线 y=2x 与反比例函数 y=m−1x（m 为常数）的图象的交点，过点 A 作 x 轴的垂线，垂足为 B，且 OB=2．
（1）求点 A 的坐标及 m 的值；
（2）已知点 P0,n0
23. 已知：如图，在 △OAB 中，OA=OB，⊙O 经过 AB 的中点 C，与 OB 交于点 D，且与 BO 的延长线交于点 E，连接 EC，CD．
（1）试判断 AB 与 ⊙O 的位置关系，并加以证明；
（2）若 tan∠E=12，⊙O 的半径为 3，求 OA 的长．

24. 甲乙两组各有 10 名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：
收集数据．
各组参赛学生每分钟输入汉字个数统计如表：
输入汉字个132133134135136137甲组人数人101521乙组人数人014122
分析数据．
两组数据的众数、中位数、平均数、方差如表所示：
组众数中位数平均数x方差s2甲组1351351351.6乙组134134.51351.8
得出结论．
（1）若每分钟输入汉字个数 136 及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?
（2）请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）．

25. 如图，在 △ABC 中，AB=4.41 cm，BC=8.83 cm，P 是 BC 上一动点，连接 AP，设 P，C 两点间的距离为 x cm，P，A 两点间的距离为 y cm．（当点 P 与点 C 重合时，x 的值为 0）
小东根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如表：
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当 PA=PC 时，PC 的长度约为 cm．（结果保留一位小数）

26. 在平面直角坐标系 xOy 中，抛物线 y=x2−3m+1x+2m2+mm>0，与 y 轴交于点 C，与 x 轴交于点 Ax1,0，Bx2,0，且 x1（1）求 2x1−x2+3 的值；
（2）当 m=2x1−x2+3 时，将此抛物线沿对称轴向上平移 n 个单位，使平移后得到的抛物线顶点落在 △ABC 的内部（不包括 △ABC 的边），求 n 的取值范围（直接写出答案即可）．

27. 如图，在等腰直角 △ABC 中，∠CAB=90∘，F 是 AB 边上一点，作射线 CF，过点 B 作 BG⊥CF 于点 G，连接 AG．
（1）求证：∠ABG=∠ACF；
（2）用等式表示线段 CG，AG，BG 之间的等量关系，并证明．

28. 在平面直角坐标系 xOy 中，过 y 轴上一点 A 作平行于 x 轴的直线交某函数图象于点 D，点 P 是 x 轴上一动点，连接 DP，过点 P 作 DP 的垂线交 y 轴于点 E（E 在线段 OA 上，E 不与点 O 重合），则称 ∠DPE 为点 D，P，E 的“平横纵直角”．图 1 为点 D，P，E 的“平横纵直角”的示意图．如图 2，在平面直角坐标系 xOy 中，已知二次函数图象与 y 轴交于点 F0,m，与 x 轴分别交于点 B−3,0，C12,0．若过点 F 作平行于 x 轴的直线交抛物线于点 N．
（1）点 N 的横坐标为 ；
（2）已知一直角为点 N，M，K 的“平横纵直角”，若在线段 OC 上存在不同的两点 M1，M2，使相应的点 K1，K2 都与点 F 重合，试求 m 的取值范围；
（3）设抛物线的顶点为点 Q，连接 BQ 与 FN 交于点 H，当 45∘≤∠QHN≤60∘ 时，求 m 的取值范围．
答案
第一部分
1. C
2. B
3. D
4. A
5. D
6. C
7. B
8. D
第二部分
9. 22−3
10. aa+ba−b
11. 答案不唯一，如 −x2+2x−1
12. a2−b2=a+ba−b
13. 480x+3×45=360x
14. 3
15. 23−2
16. SSS 公理，全等三角形的对应角相等
第三部分
17. 2x+3≤4x+7, ⋯⋯①x+22>x. ⋯⋯②
由 ①，得
x≥−12.
由 ②，得
x<2.
所以原不等式组的解集为
−12≤x<2.
它的所有整数解为 0，1．
18. 4S；4S；2S2
19. ∵AB=AC，
∴∠B=∠C．
∵∠B=50∘，
∴∠C=50∘．
∴∠BAC=180∘−50∘−50∘=80∘．
∵∠BAD=55∘，
∴∠DAE=25∘．
∵DE⊥AD，
∴∠ADE=90∘．
∴∠DEC=∠DAE+∠ADE=115∘．
20. （1） 根据题意，得
Δ=−62−4×31−k≥0.
解得
k≥−2.∵k
为负整数，
∴k=−1，−2．
（2） 当 k=−1 时，不符合题意，舍去；
当 k=−2 时，符合题意，此时方程的根为 x1=x2=1．
21. （1） ∵CE∥OD，DE∥OC ，
∴ 四边形 OCED 是平行四边形，
又 ∵ 四边形 ABCD 是矩形，
∴AC=BD，OC=12AC，OB=12BD，
∴OC=OD，
∴ 平行四边形 OCED 是菱形.
（2） 在矩形 ABCD 中，∠ABC=90∘，∠BAC=30∘，AC=4，
∴ BC=2 .
∴ AB=DC=23 .
连接 OE，交 CD 于点 F .
∵ 四边形 OCED 为菱形，
∴ F 为 CD 中点.
∵ O 为 BD 中点，
∴ OF=12BC=1 .
∴ OE=2OF=2 .
∴S菱形OCED=12OE⋅CD=12×2×23
=23
22. （1） 由题意得，可知点 A 的横坐标是 2，
由点 A 在正比例函数 y=2x 的图象上，
∴ 点 A 的坐标为 2,4，
又 ∵ 点 A 在反比例函数 y=m−1x 的图象上，
∴4=m−12，即 m=9．
（2） 623. （1） AB 与 ⊙O 的位置关系是相切．
证明：如图，连接 OC．
因为 OA=OB，C 为 AB 的中点，
所以 OC⊥AB，
所以 AB 是 ⊙O 的切线．
（2） 因为 ED 是直径，
所以 ∠ECD=90∘，
所以 ∠E+∠ODC=90∘．
又因为 ∠BCD+∠OCD=90∘，∠OCD=∠ODC，
所以 ∠BCD=∠E．
又因为 ∠CBD=∠EBC，
所以 △BCD∽△BEC，
所以 BCBE=BDBC，
所以 BC2=BD⋅BE，
因为 tan∠E=12，
所以 CDEC=12．
因为 △BCD∽△BEC，
所以 BDBC=CDEC=12．
设 BD=x，则 BC=2x，
又 BC2=BD⋅BE，
所以 2x2=xx+6，解得 x1=0，x2=2．
因为 BD=x>0，
所以 BD=2．
所以 OA=OB=BD+OD=2+3=5．
24. （1） 乙组成绩更好一些．
（2） 答案不唯一，评价需支撑推断结论．
25. （1） 4.6（答案不唯一）
（2） 如图所示．
（3） 4.4（答案不唯一）
26. （1） 解关于 x 的一元二次方程，x2−3m+1x+2m2+m=0．
得 x=2m+1，x=m，
∵m>0，x1 ∴x1=m，x2=2m+1．
2x1−x2+3=2m−2m−1+3=2．
（2） 符合题意的 n 的取值范围是 9427. （1） ∵∠CAB=90∘，
∵BG⊥CF 于点 G，
∴∠BGF=∠CAB=90∘．
∵∠GFB=∠CFA，
∴∠ABG=∠ACF．
（2） CG=2AG+BG．
证明：在 CG 上截取 CH=BG，连接 AH，
∵△ABC 是等腰直角三角形，
∴∠CAB=90∘，AB=AC．
∵∠ABG=∠ACH，
∴△ABG≌△ACH．
∴AG=AH，∠GAB=∠HAC．
∴∠GAH=90∘．
∴AG2+AH2=GH2．
∴GH=2AG．
∴CG=CH+GH=2AG+BG．
28. （1） 9
（2） 方法一：
∵MK⊥MN，
∴ 要使线段 OC 上存在不同的两点 M1，M2，使相应的点 K1，K2 都与点 F 重合，也就是使以 FN 为直径的圆与 OC 有两个交点，即 r>∣m∣．
∴r=92，
∴∣m∣<92．
又 ∵m>0，
∴0【解析】方法二：
∵m>0，
∴ 点 K 在 x 轴的上方．
过 N 作 NW⊥OC 于点 W，
设 OM=x，OK=y，
则 CW=OC−OW=3，WM=9−x．
由 △MOK∽△NWM，得，OKWM=MONW，
∴y9−x=xm．
∴y=−1mx2+9mx．
当 y=m 时，m=−1mx2+9mx，
化为 x2−9x+m2=0．
当 Δ=0，即 92−4m2=0，
解得 m=92 时，
线段 OC 上有且只有一点 M，使相应的点 K 与点 F 重合．
∵m>0，
∴ 线段 OC 上存在不同的两点 M1，M2，使相应的点 K1，K2 都与点 F 重合时，m 的取值范围为 0 （3） 设抛物线的表达式为：y=ax+3x−12a≠0，
又 ∵ 抛物线过点 F0,m，
∴m=−36a．
∴a=−136m．
∴y=−136mx+3x−12=−136mx−922+2516m．
过点 Q 做 QG⊥x 轴与 FN 交于点 R，
∵FN∥x 轴，
∴∠QRH=90∘，
∵tan∠BQG=BGQG，QG=2516m，BG=152，
∴tan∠BQG=245m，
又 45∘≤∠QHN≤60∘，
∴30∘≤∠BQG≤45∘，
∴ 当 ∠BQG=30∘ 时，可求出 m=2453，
当 ∠BQG=45∘ 时，可求出 m=245．
∴m 的取值范围为 245≤m≤2453．