2018年上海市徐汇区中考二模数学试卷（期中）

这是一份2018年上海市徐汇区中考二模数学试卷（期中），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共6小题；共30分）
1. 下列算式的运算结果正确的是
A. m3⋅m2=m6B. m5÷m3=m2m≠0
C. m−23=m−5D. m4−m2=m2

2. 直线 y=3x+1 不经过的象限是
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

3. 如果关于 x 的方程 x2−kx+1=0 有实数根，那么 k 的取值范围是
A. k>0B. k≥0C. k>4D. k≥4

4. 某射击选手 10 次射击成绩统计结果如表，这 10 次成绩的众数、中位数分别是
成绩环78910次数1432
A. 8，8B. 8，8.5C. 8，9D. 8，10

5. 如果一个正多边形内角和等于 1080∘，那么这个正多边形的每一个外角等于
A. 45∘B. 60∘C. 120∘D. 135∘

6. 下列说法中，正确的个数共有
（1）一个三角形只有一个外接圆；
（2）圆既是轴对称图形，又是中心对称图形；
（3）在同圆中，相等的圆心角所对的弧相等；
（4）三角形的内心到该三角形三个顶点距离相等．
A. 1 个B. 2 个C. 3 个D. 4 个

二、填空题（共12小题；共60分）
7. 函数 y=1x−2 的定义域是 ．

8. 在实数范围内分解因式：x2y−2y= ．

9. 方程 x−3=2 的解是 ．

10. 不等式组 −2x≥6,x+7>−2 的解集是 ．

11. 已知点 Aa,y1，Bb,y2 在反比例函数 y=3x 的图象上，如果 a
12. 抛物线 y=2x2+4x−2 的顶点坐标是 ．

13. 四张背面完全相同的卡片上分别写有 0.3，9，2，227 四个实数，如果将卡片字面朝下随意放在桌子上，任意取一张，那么抽到有理数的概率为 ．

14. 在 △ABC 中，点 D 在边 BC 上，且 BD:DC=1:2，如果设 AB=a，AC=b，那么 BD 等于 （结果用 a，b 的线性组合表示）．

15. 如图，为了解全校 300 名男生的身高情况，随机抽取若干男生进行身高测量，将所得数据（精确到 1 cm）整理画出频数分布直方图（每组数据含最低值，不含最高值），估计该校男生的身高在 170 cm∼175 cm 之间的人数约有 人．

16. 已知两圆相切，它们的圆心距为 3，一个圆的半径是 4，那么另一个圆的半径是 ．

17. 从三角形（非等腰三角形）一个顶点引出一条射线与对边相交，该顶点与该交点间的线段把这个三角形分割成两个小三角形，如果其中一个小三角形是等腰三角形，另一个与原三角形相似，那么我们把这条线段叫做这个三角形的完美分割线，如图，在 △ABC 中，DB=1，BC=2，CD 是 △ABC 的完美分割线，且 △ACD 是以 CD 为底边的等腰三角形，则 CD 的长为 ．

18. 如图，在 Rt△ABC 中，∠C=90∘，AB=5，BC=3，点 P，Q 分别在边 BC，AC 上，PQ∥AB，把 △PCQ 绕点 P 旋转得到 △PDE（点 C，Q 分别与点 D，E 对应），点 D 落在线段 PQ 上，若 AD 平分 ∠BAC，则 CP 的长为 ．

三、解答题（共7小题；共91分）
19. 计算：12−12−1+13−1−π−3.140+∣23−4∣．

20. 解分式方程：x−2x+2+1=16x2−4．

21. 如图，在 Rt△ABC 中，∠C=90∘，AC=3，BC=4，AD 平分 ∠BAC 交 BC 于点 D．
（1）求 tan∠DAB；
（2）若 ⊙O 过 A，D 两点，且点 O 在边 AB 上，用尺规作图的方法确定点 O 的位置并求出的 ⊙O 半径．（保留作图轨迹，不写作法）

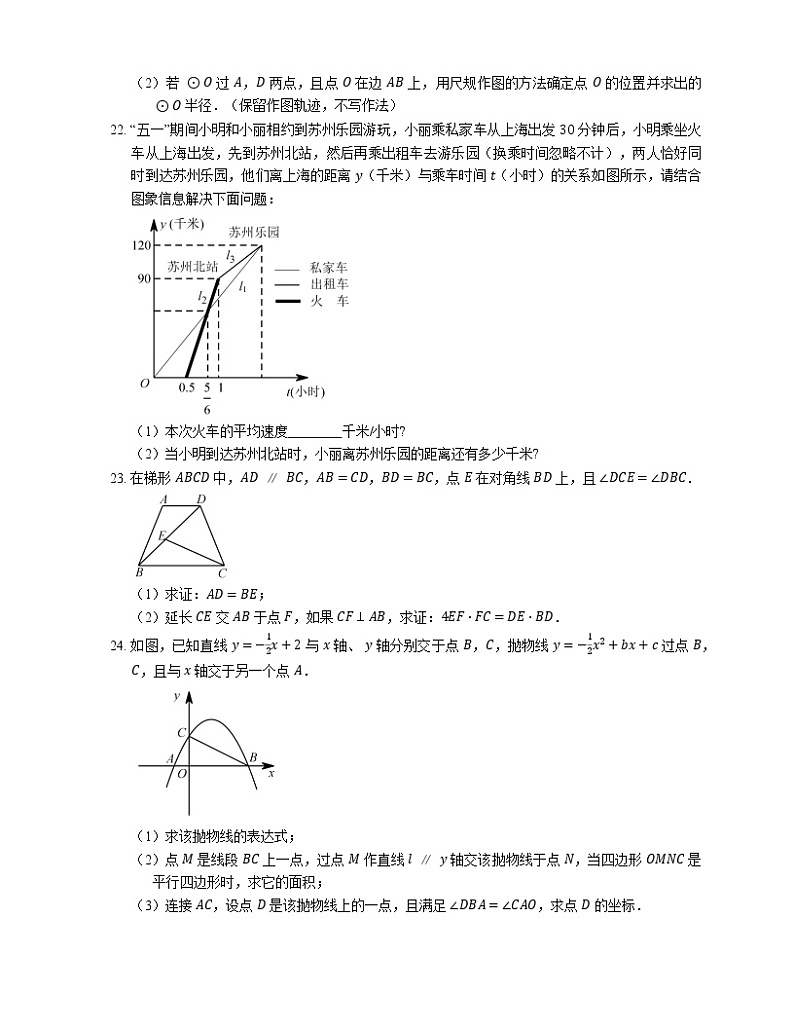
22. “五一”期间小明和小丽相约到苏州乐园游玩，小丽乘私家车从上海出发 30 分钟后，小明乘坐火车从上海出发，先到苏州北站，然后再乘出租车去游乐园（换乘时间忽略不计），两人恰好同时到达苏州乐园，他们离上海的距离 y（千米）与乘车时间 t（小时）的关系如图所示，请结合图象信息解决下面问题：
（1）本次火车的平均速度 千米/小时?
（2）当小明到达苏州北站时，小丽离苏州乐园的距离还有多少千米?

23. 在梯形 ABCD 中，AD∥BC，AB=CD，BD=BC，点 E 在对角线 BD 上，且 ∠DCE=∠DBC．
（1）求证：AD=BE；
（2）延长 CE 交 AB 于点 F，如果 CF⊥AB，求证：4EF⋅FC=DE⋅BD．

24. 如图，已知直线 y=−12x+2 与 x 轴、 y 轴分别交于点 B，C，抛物线 y=−12x2+bx+c 过点 B，C，且与 x 轴交于另一个点 A．
（1）求该抛物线的表达式；
（2）点 M 是线段 BC 上一点，过点 M 作直线 l∥y 轴交该抛物线于点 N，当四边形 OMNC 是平行四边形时，求它的面积；
（3）连接 AC，设点 D 是该抛物线上的一点，且满足 ∠DBA=∠CAO，求点 D 的坐标．

25. 已知四边形 ABCD 是边长为 10 的菱形，对角线 AC，BD 相交于点 E，过点 C 作 CF∥DB 交 AB 延长线于点 F，连接 EF 交 BC 于点 H．
（1）如图 1，当 EF⊥BC 时，求 AE 的长；
（2）如图 2，以 EF 为直径作 ⊙O，⊙O 经过点 C 交边 CD 于点 G（点 C，G 不重合），设 AE 的长为 x，EH 的长为 y；
①求 y 关于 x 的函数关系式，并写出定义域；
②连接 EG，当 △DEG 是以 DG 为腰的等腰三角形时，求 AE 的长．
答案
第一部分
1. B
2. D
3. D
4. B
5. A
6. C
第二部分
7. x≠2
8. yx+2x−2
9. x=7
10. −911. >
12. −1,−4
13. 34
14. 13b−13a
15. 72
16. 1 或 7
17. 32
18. 2
【解析】连接 AD，
∵PQ∥AB，
∴∠ADQ=∠DAB．
∵ 点 D 在 ∠BAC 的平分线上，
∴∠DAQ=∠DAB，
∴∠ADQ=∠DAQ，
∴AQ=DQ．
在 Rt△ABC 中，
∵AB=5，BC=3，
∴AC=4，
∵PQ∥AB，
∴△CPQ∽△CBA，
∴CP:CQ=BC:AC=3:4，设 PC=3x，CQ=4x，
在 Rt△CPQ 中，PQ=5x，
∵PD=PC=3x，
∴DQ=2x．
∵AQ=4−4x，
∴4−4x=2x，解得 x=23，
∴CP=3x=2．
第三部分
19. 原式=23−2+3+12−1+4−23=3+32.
20. 化为整式方程得：
x2−4x+4+x2−4=16.x2−2x−8=0.
解得：
x1=−2,x2=4.
经检验 x=−2 时，x+2=0，
∴x=4 是原方程的解．
21. （1） 过点 D 作 DE⊥AB 于 E，
∵AD 平分 ∠BAC，
∴CD=DE，
在 Rt△ACD 和 Rt△AED 中，
AD=AD,CD=DE,
∴Rt△ACD≌Rt△AEDHL，
∴AE=AC=3，
由勾股定理得，AB=32+42=5，
∴BE=AB−AE=5−3=2，
设 CD=DE=x，则 BD=4−x，
在 Rt△BDE 中，DE2+BE2=BD2，
x2+22=4−x2，解得 x=32，即 CD 的长为 32，
∴Rt△ACD 中，tan∠DAC=CDAC=12，
∴tan∠DAB=12．
（2） 如图，点 O 即为所求，连接 OD，
∵OA=OD，
∴∠OAD=∠ODA，
∵AD 平分 ∠BAC，
∴∠OAD=∠CAD，
∴∠CAD=∠ODA，
∴OD∥AC，
∴△BDO∽△BCA，
∴BOBA=ODAC，
设 OD=AO=r，则 BO=5−r，
∴5−r5=r3，
∴r=158，即 ⊙O 半径为 158．
22. （1） 180
【解析】v=901−0.5=180．
故本次火车的平均速度是每小时 180 千米．
（2） 设 l2 的解析式为 y=kt+b，
∵ 当 t=0.5 时，y=0，当 t=1 时，y=90，
∴0.5k+b=0,k+b=90, 解得：k=180,b=−90,
∴l2 的解析式为 y=180t−90，
把 t=56 代入，得 y=180×56−90=60，
∵56,60 在直线 l1 上，
∴ 直线 l1 的解析式为 y=72t，
∴ 当 t=1 时，y=72，120−72=48（千米），
故当小明到达苏州北站时，小丽离苏州乐园的距离还有 48 千米．
23. （1） ∵AB=CD，AD∥BC，
∴∠ABC=∠DCB，∠ADB=∠EBC．
∵∠DCE=∠DBC，∠ABC=∠ABD+∠DBC，∠DCB=∠DCE+∠ECB，
∴∠ABD=∠ECB．
在 △ABD 和 △ECB 中，
∠ADB=∠EBC,BD=CB,∠ABD=∠ECB,
∴△ABD≌△ECBASA，
∴AD=BE．
（2） 连接 AC，
∵AD∥BC，AB=CD，
∴ 四边形 ABCD 是等腰梯形，
∴AC=BD，
∵BD=BC，
∴AC=BC，
∵CF⊥AB，
∴BF=AF，
∴BF=12AB，
∵∠DCE=∠DBC，
∴△DCE∽△DBC，
∴CDDB=DECD，
∴CD2=DB⋅DE，
∵∠DCE=∠DBC，
∴∠FBE=∠FCB，
∴△BFE∽△CFB，
∴BFCF=EFBF，
∴BF2=CF⋅EF，
∵BF2=14AB2=14CD2，
∴14CD2=CF⋅EF，
∴14DE⋅DB=CF⋅EF，
∴4EF⋅FC=DE⋅BD．
24. （1） 当 x=0 时，y=2，
∴C0,2，
当 y=0 时，−12x+2=0，x=4，
∴B4,0，
把 C0,2 和 B4,0 代入抛物线 y=−12x2+bx+c 中得：c=2,−12×42+4b+c=0,
解得：b=32,c=2,
∴ 该抛物线的表达式：y=−12x2+32x+2．
（2） 如图 1，
∵C0,2，
∴OC=2，
设 Mm,−12m+2，则 Nm,−12m2+32m+2，
∴MN=−12m2+32m+2−−12m+2=−12m2+2m，
∵MN∥y 轴，
当四边形 OMNC 是平行四边形时，MN=OC，
即 −12m2+2m=2，解得：m1=m2=2，
∴S平行四边形OCMN=OC×2=2×2=4．
（3） 分两种情况：
当 y=0 时，−12x2+32x+2=0，解得：x1=4，x2=−1，
∴A−1,0，
易得直线 AC 的解析式为：y=2x+2，
①当 D 在 x 轴的下方时，如图 2，AC∥BD，
∴ 设直线 BD 的解析式为：y=2x+b，
把 B4,0 代入得：0=2×4+b，b=−8，
∴ 直线 BD 的解析式为：y=2x−8，
则 2x−8=−12x2+32x+2，解得：x1=−5，x2=4（舍），
∴D−5,−18；
②当 D 在 x 轴的上方时，如图 3，作抛物线的对称轴交直线 BD 于 M，交 BE（图 2 中的点 D）于 N，
对称轴是：x=−322×−12=32，
∵∠CAO=∠ABE=∠DBA，
∴M 与 N 关于 x 轴对称，
直线 BE 的解析式：y=2x−8，当 x=32 时，y=−5，
∴N32,−5，M32,5，
直线 BM 的解析式为：y=−2x+8，
−2x+8=−12x2+32x+2，解得：x1=3，x2=4（舍），
∴D3,2，
综上所述，点 D 的坐标为：−5,−18 或 3,2．
25. （1） ∵ 四边形 ABCD 是菱形，
∴DC∥AB，AB=DC，DB 和 AC 互相垂直平分，
∵CF∥DB，
∴ 四边形 DBFC 是平行四边形，
∴BF=DC=AB=10，
∴∠CAB=∠BCA，
当 EF⊥BC 时，∠CAB=∠BCA=∠CFE，
∴Rt△AFC∽Rt△FEC，
∴FC2=CE⋅AC，即 FC2=2AE2，
Rt△ACF 中，CF2+AC2=AF2，2AE2+4AE2=400，
解得：AE=1063．
（2） ①如图 3，连接 OB，
则 AB=BF，OE=OF，
∴OB∥AC，且 OB=12AE=12EC=12x，
∴OHEH=OBEC=12，
∴EH=23EO，
在 Rt△EBO 中，EO2=BE2+OB2=100−x22+12x2=−34x2+100，
∴y=23EO=400−3x231063②当 GD=GE 时，有 ∠GDE=∠GED，
∵AC⊥DB，∠DEC=90∘，
∴∠GCE=∠GEC，
∴GE=GC，
∴GD=GC，即 G 为 DC 的中点，
又 ∵EO=FO，
∴GO 是梯形 EFCD 的中位线，
∴GO=DE+CF2=32DE，
∴32y=32100−x2，
∴400−3x22=32100−x2，
解得：x=5303；
如图 4，当 DE=DG 时，连接 OD，OC，GO，
在 △GDO 和 △EDO 中，
∵DG=DE,DO=DO,OG=OE,
∴△GDO≌△EDOSSS，
∴∠DEO=∠DGO，
∴∠CGO=∠BEO=∠OFC，
∴∠CGO=∠OCG=∠OFC=∠OCF，
∴GC=CF，
∴DC=DG+GC=DE+2DE=10，
即 3100−x2=10，解得：x=2023，
综上，AE 的长为 5303 或 2023．